Fractions
WHAT ARE FRACTIONS?

A fraction in everyday language is a part of a whole thing. … read more
A fraction in everyday language is a part of a whole thing. We think of fractions as numbers that look like 1/2 or 3/5. Mathematically, a fraction is a number that can be written in a form (a/b) with certain conditions. The numerator and denominator must be whole numbers and since division by zero is problematic, the denominator cannot be zero. Using this definition, 1/2 and 3/5 are clearly fractions. However, it is important to note that 5/5 and 5/4 are also fractions.
There is significant research-based evidence that students develop fractional concepts through the use of multiple conceptual representations, including fraction circles, number lines and drawings. Students make connections among these representations as well as to written symbols. Students use the models to develop concepts about the unit whole, equal parts of the whole, order, and equivalence before developing procedures for translating between symbols or computing with fractions (National Research Council, 2001; Lamon, 2006; Cramer, Post, and delMas, 2002; Cramer and Wyberg, 2012).
Types of Fractions
A fraction can represent any of the following depending on the context… read more
Types of Fractions
A fraction can represent any of the following depending on the context:
- number of parts of a whole
- a point on a number line
- indication of division
- pure number
- ratio, or comparison of one quantity to another
- probability
Fractions that tell the number of parts of a whole are known as part-whole fractions. It is important for students to understand what is meant by the whole for a given part-whole fraction. For example, the whole can be either a single thing (as with 2/3 of a pizza) or a set of separate things (as with 1/2 of all the students in a class). Fractions can also be shown as locations on a number line that lie between whole-number locations. This representation shows the numerical value of fractions relative to other fractions and benchmark numbers (e.g., 0, 1/2, and 1).
Students need to understand that although fractions occur in different situations, the mathematical procedures for naming, comparing, and operating on fractions are the same. To make connections among the various contexts in which fractions arise, students explore fractions using a broad selection of concrete materials. In this unit, students use a part-whole model (circle pieces) to review concepts developed in previous grades and to investigate mixed numbers and improper fractions. They also use a number line model to compare fractions and to find equivalent fractions.
MULTIPLE REPRESENTATIONS

Students need exposure to a variety of concrete models and mathematical interpretations… read more
Students need exposure to a variety of concrete models and mathematical interpretations of fractions in order to understand the underlying concepts before they can develop meaningful procedures with symbols (Cramer, et al., 1997). Therefore, in this unit, students develop concepts and procedures for working with fractions using fraction circles, drawings, and number lines.
Research suggests that though students are able to draw on their informal or “real-life” knowledge of fractions to solve problems, premature attempts at using symbolic procedures can interfere with the construction of meaningful algorithms (Mack, 1990). For example, when students are presented with a problem such as 4 − 3/4, their answers are often incorrect because they try to apply rote procedures based on a whole-number algorithm. The same students are often able to solve the problem when it is presented in a context, such as:
Maya has 4 cookies. She ate 3/4 of a cookie after lunch. How many cookies does she have left?
They use their knowledge of the real world to think through the problem using context and imagery, and then find a solution that makes sense to them.
Circle Pieces
In this unit, students use circle pieces to represent fractions. … read more
Circle Pieces
In this unit, students use circle pieces to represent fractions. Circle pieces provide an area model for part-whole fractions that students can manipulate, visualize, and experiment with as they explore fraction concepts. Research conducted by Rational Number Project at the University of Minnesota (Cramer and Wyberg, 2012) demonstrates that the circle model is especially useful for students to construct mental images of fractions, compare fractions, and estimate sums and differences. See Figure 1.
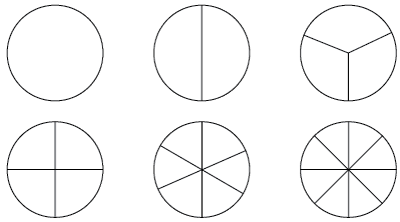
Figure 1: A sample of fraction circle pieces
Number Lines
Locating fractions on number lines helps reinforce the fact that fractions are numbers… read more
Number Lines
Locating fractions on number lines helps reinforce the fact that fractions are numbers, just as whole numbers are. Number lines give a visual representation of numbers in increasing order that helps students understand the relative size of fractions.
To represent fractions on the number line, divide the interval from zero to one into equal parts. Then label each mark to show what fraction of the distance from 0 to 1 it is. Figure 2 shows fifths on the number line. The interval from 0 to 1 is divided into five parts. The length of each part is one fifth of the distance from 0 to 1. The label 1/5 is at the place that is 1/5 of the distance from 0 to 1, 2/5 is at the place that is 2/5 of the distance from 0 to 1, and so on.

Figure 2: Showing fifths on the number line
In this unit, students work with number lines to find equivalent fractions. When fractions are represented on number lines, two fractions are equivalent if they are the same distance from 0. Equivalent fractions can label the same point on the number line. The number lines in Figure 3 show that 1/2 and 2/4 are equivalent because they are the same distance from 0.
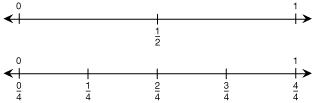
Figure 3: Number lines showing halves and fourths
Students will also use number lines to compare fractions. The number lines in Figure 3 show that 3/4 is greater than 1/2 because it is farther from 0.
Number lines continue beyond 1 and the method for showing fractions can be continued as well. Figure 4 shows the fraction 11/4. It is easy to see that it is equivalent to the mixed number 23/4.

Figure 4: Number line showing halves and fourths
ADDING and SUBTRACTING FRACTIONS

As students begin performing operations on fractions, it is important… read more
As students begin performing operations on fractions, it is important that they do so with a foundational number sense about fractions. The development of fluency with addition and subtraction of fractions follows from an understanding about the relative sizes of fractions, about how fractions can be broken apart, and about how to estimate answers to addition and subtraction problems. The extended use of concrete models, particularly fraction circle pieces, supports all three of these understandings.
In this unit, students practice breaking fractions apart and putting them together through playing games with fraction circle pieces and number lines. This activity allows students to develop skills in breaking up and re-assembling fractions using circle pieces and number sentences as shown in Figure 5.
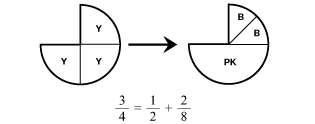
Figure 5: Composing and decomposing 3/4 using circle pieces
Research conducted by the Rational Number Project has shown that students' learning about fractions and fraction operations is optimized through use of concrete models over extended periods of time (Cramer et al. 1997). Extended use of concrete models such as fraction circle pieces allows students to build the mental images needed to think conceptually about fractions. Students' work with addition and subtraction of fractions in this unit therefore focuses on building a conceptual foundation before moving to formal work with symbols and algorithms. These pre-formal strategies foradding and subtracting fractions include:
- Estimating answers to problems using mental images of fraction circle pieces,
- Modeling problems with circle pieces,
- Inventing strategies with circle pieces to find exact answers to problems,
- Using a one-color replacement strategy to find exact answers to problems, and
- Constructing number sentences from manipulations with circle pieces.
All of these strategies represent a progression that builds number sense, mental math, and flexible thinking about fractions. At the same time, these strategies lay the foundation of understanding for a more numerical, paper-and-pencil approach to adding and subtracting fractions. The strength of the progression lies in allowing students time to work with the manipulatives to build imagery and meaning for the common-denominator algorithm before formally introducing it.
“Instructional practices that tend toward premature abstraction and extensive symbolic manipulation lead students to have severe difficulty in representing rational numbers with standard written symbols and using the symbols appropriately” (National Research Council, 2001, p. 234).
MATH FACTS and MENTAL MATH

This unit begins the review and assessment of the division facts… read more
This unit begins the review and assessment of the division facts to develop mental math strategies, gain fluency, and to learn to apply multiplication and division strategies to larger numbers. Students will focus on the division facts for the 5s and 10s.
Resources
- Cramer, K., M. Behr, T. Post, and R. Lesh. Rational Number Project: Fraction Lessons for the Middle Grades – Level 1 <http://cehd.umn.edu/rationalnumberproject/rnp1.html>. Kendall/Hunt Publishing Co., Dubuque, Iowa, 1997.
- Cramer, K., and T.R. Post. “Making Connections: A Case for Proportionality.” In Arithmetic Teacher. 40(6), National Council of Teachers of Mathematics. Reston, VA, 1993.
- Cramer, K., T.R. Post, and R.C. delMas, “Initial Fraction Learning by Fourth- and Fifth-Grade Students: A Comparison of the Effects of Using Commercial Curricula With the Effects of Using the Rational Number Project Curriculum.” In Journal for Research in Mathematics Education. 33(2), 111–144, 2002.
- Cramer, K., and T. Wyberg. “Efficacy of Different Concrete Models for Teaching the Part-Whole Construct for Fractions.” Mathematical Thinking and Learning, 11(4), 226–257, 2012.
- Curcio, F.R., and N.S. Bezuk. Understanding Rational Numbers and Proportions. National Council of Teachers of Mathematics, Reston, VA, 1994.
- Lamon, Susan J. “Fractions and Rational Numbers.” In Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers. Lawrence Erlbaum Associates, Mahwah, New Jersey, 2006.
- Mack, N.K. “Learning Fractions with Understanding: Building on Informal Knowledge.” In Journal for Research in Mathematics Education. 21(1), National Council of Teachers of Mathematics. Reston, VA, 1990.
- National Research Council. “Developing Proficiency With Other Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, Eds. National Academy Press, Washington D.C., 2001.
- Post, T.R., et al. “Order and Equivalence of Rational Numbers: A Cognitive Analysis.” In Journal for Research in Mathematics Education. 16(1), National Council of Teachers of Mathematics. Reston, VA, 1990.
- Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- Wu, Hung-Hsi. Chapter 2: Fractions (Draft) (June 20, 2001; Revised September 3, 2002).











