Lesson 11

Subtract Fractions

Est. Class Sessions: 2

Developing the Lesson

Part 2. Subtracting Fractions to Solve Problems

Read the opening vignette about Mr. Moreno's aquarium on the Subtract Fractions pages in the Student Guide. Ask students to work with a partner to estimate whether the can of fish food will be more or less than 1/2 full at the end of the week (Question 1). Read Jacob's method for estimating the answer to the problem with the class.

Ask:

X
  • How does your estimate compare with Jacob's? [Question 2]
  • Did you use the same strategy as Jacob?
  • How was your strategy similar to Jacob's? How was it different?

Have students model and solve the problem to find an exact answer using fraction circle pieces (Question 3). Remind students to write number sentences for their solutions and to compare their exact answers to their estimates. Ask several students to share their strategies with the class using display circle pieces. Read Keenya's method for solving the problem with the class. Discuss how Jacob's estimate agrees with Keenya's exact answer (Question 4).

Ask:

X
  • Whose method from our class is most like Keenya's?

Next, read Julia's method for solving the problem. Julia uses multiplication to find an equivalent fraction with a common denominator.

Ask:

X
  • Whose method from our class is most like Julia's?
  • How are Keenya's and Julia's methods similar? How are they different [Question 5]? (Possible response: Keenya uses the single-color method with circle pieces. Julia finds a common denominator with multiplication, which is similar, but she just uses paper and pencil.)

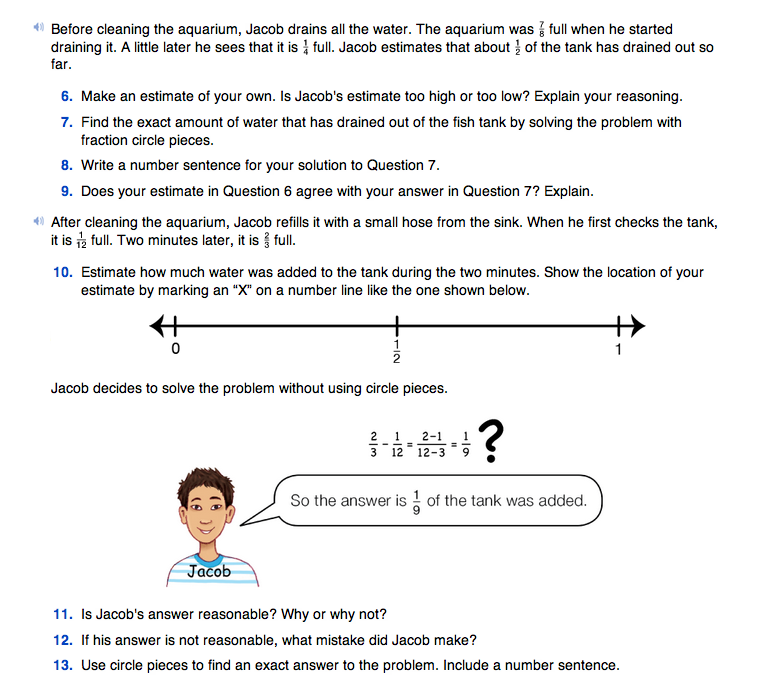
Have students work with partners to solve Questions 6–8. Discuss students' estimates and solutions using Question 9.

Questions 10–13 lead students to identify a common misconception in a procedure for subtracting fractions. As with fraction addition, a common mistake is to try to perform the operation on the numerators and the denominators separately. Students identify that this method leads to an answer that is not reasonable, and that it does not make sense in terms of the circle pieces model. Students find an exact answer using fraction circle pieces in Question 13.

Have a student use circle pieces to model their solution to the problem 2/3 − 1/12 . If a method other than the single-color method is used, ask another student to show how 2 orange pieces ( 2/3 of the circle) can be replaced with 8 black pieces ( 8/12 ). 1 black piece can be removed to leave 7 of the pieces ( 8/12 − 1/12 = 7/12 ). Then make the connection between the single-color method and using multiplication to find equivalent fractions with common denominators.

Ask:

X
  • Is it easier to subtract circle pieces of all one color or of different colors? (all one color)
  • How did you decide which single color to use? (Possible response: Since I had to take one black piece away, I wanted to make all the pieces black. 2 orange pieces is the same as 8 black pieces.)
  • Would it help to replace the 2 orange pieces with aqua pieces? Why or why not? (No, because I can't easily take one black piece from 4 aqua pieces. I can take 1 black piece from 8 black pieces though.)
  • How can the single-color method help you think about common denominators? (Finding one common color to use is like finding one common denominator to use.)
  • 2/3 is equivalent to 4/6 , but does 4/6 − 1/12 make it easier to solve the problem? Why or why not? (No; It is easier to subtract fractions with like denominators.)
  • Let's find equivalent fractions with common denominators to solve 2/3 − 1/12. Can 2/3 be renamed as twelfths? What can you multiply the denominator in 2/3 by to get twelfths? (Possible response: To find an equivalent fraction, multiply both the numerator and the denominator by the same number. Since 3 × 4 = 12, you have to multiply the numerator 2 × 4 also. 2/3 is equivalent to 8/12 .)
  • What do you notice about the denominators 3 and 12? (They are multiples of 3. 3 × 1 = 3 and 3 × 4 = 12.)
  • How can you rewrite the number sentence using fractions with common denominators? ( 8/12 − 1/12 = 7/12 )

Assign Check-In: Questions 14–20. In these questions, students practice solving more subtraction problems. Remind students to first estimate answers relative to benchmark numbers of 0, 1/2 , or 1. Question 19 provides more practice with fraction subtraction and writing number sentences. In Question 20, students explain their solution strategies.

X

Use Check–In: Questions 14–20 on the Subtract Fractions pages of the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to find equivalent fractions using tools and multiplication and division strategies [E4]; subtract fractions including those with unlike denominators [E7]; use visual models or equations to represent the solution for word problems involving subtracting fractions [E8]; and use benchmark fractions to estimate differences and assess the reasonableness of answers [E9].

Question 20 can be used to assess students' abilities to find a strategy [MPE2] and show work [MPE5].

Student Guide: 100 101 102 103
Answers
X
SG_Mini
+
X
SG_Mini
+
X
SG_Mini
+
X
SG_Mini
+
Student Activity Book:
Master: