Equivalent Fractions on Number Lines

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Fraction Trails

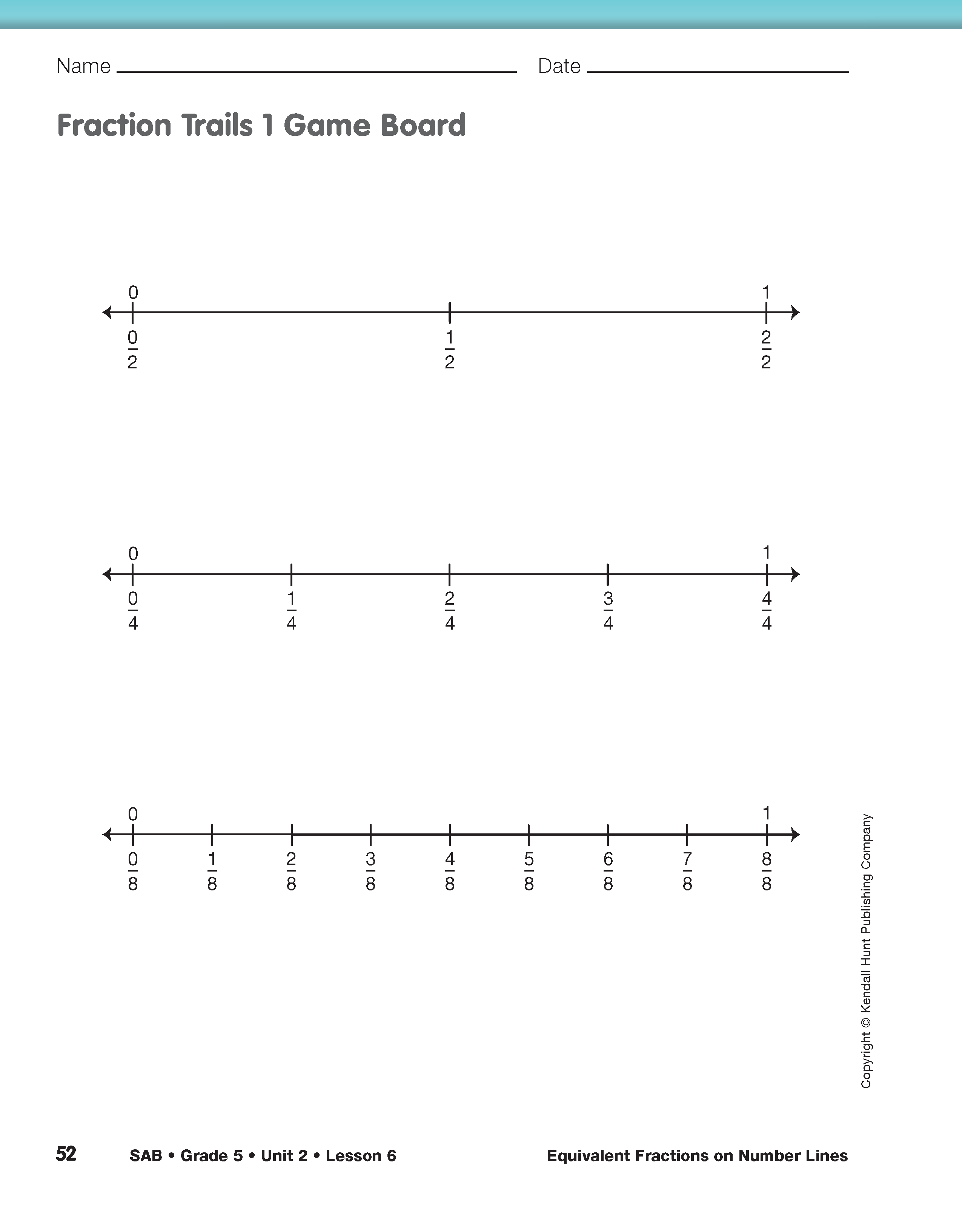
Introduce and Play Fraction Trails 1 Game. Fraction Trails Games develop the same concepts as the Fraction Fill Games in Lesson 4, but students use number lines instead of circles to represent fractions. Game 1 involves halves, fourths, and eighths. Game 2 involves halves, thirds, sixths, and twelfths. Game 3 involves all the fractions from the first two games. Encourage students to use the Fractions on Number Lines Chart in the Student Guide to help find equivalent fractions. Remind them that the same chart can also be found in the Student Guide Reference section.

Direct students to the first page of the Fraction Trails Games in the Student Activity Book. Introduce the game by reading steps 1 and 2 of the directions for the Fraction Trails 1 game. Players spin Spinner 1 on the Fraction Games Spinners pages in the Student Activity Book. They move one or more markers a total distance equal to the fraction shown on the spinner. The goal is to move a marker so that it lands exactly on 1 whole on any number line trail to earn a point.

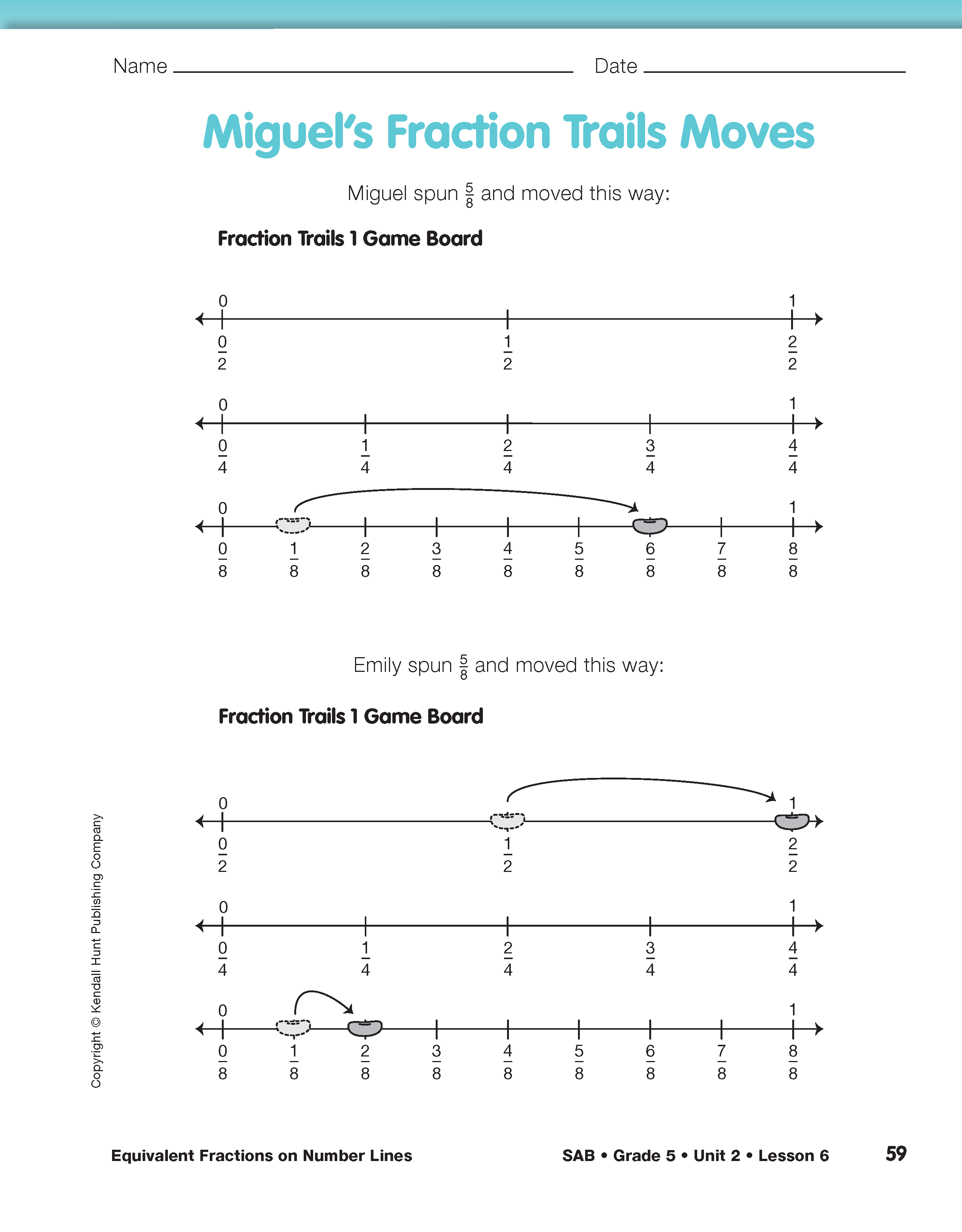
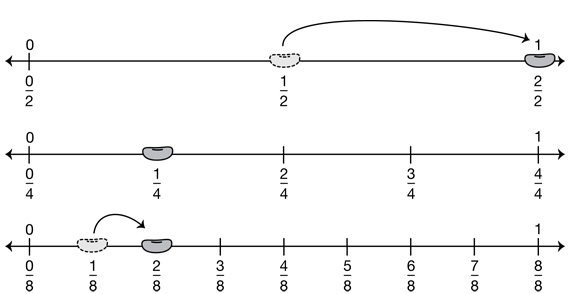
Before reading the example, display the Fraction Trails 1 Game Board on the second page of the Fraction Trails Games pages and place a marker on 1/2, 1/4, and 1/8 as in the example. See Figure 2. Ask students to suggest ways to move 5/8 on the trails. There are several ways to do this. A player can move the marker from 1/8 to 6/8. Or, by breaking 5/8 into the sum of smaller fractions (1/8 + 4/8), a player can move 1/8 on one number line trail. Then the understanding that 4/8 is equivalent to 1/2 allows the player to move 1/2 on the halves trail and earn one point.

After demonstrating the example problem, finish reading the directions and assign partners. Students will play a round of Fraction Trails 1. As they play, circulate about the room listening for use of strategies that involve equivalent fractions and breaking fractions into the sums of smaller fractions.

Discuss Game Strategies. After students have played a round, take a little time to discuss the strategies they used during the game. Display the Fraction Trails 1 Game Board and have markers ready.

Display and refer to the strategies students generated on chart paper for finding equivalent fractions and ask:

Imagine spinning 3/4. How can you find an equivalent fraction? (Possible response: I can multiply both the numerator and the denominator by 2 to make 6/8.)
Imagine spinning 1/4. Explain how to find an equivalent fraction. (Possible response: I thought about circle pieces. I thought about 1/4 of a circle and then I thought about cutting it in half to make 2/8. 1/4 and 2/8 cover the same part of the circle.)
Now think about how breaking fractions into the sums of smaller fractions can help. Imagine spinning 7/8. Which fractions can you add together to make 7/8? List the number sentences on a display.
(1/8 + 6/8 = 7/8; 2/8 + 5/8 = 7/8 ; 3/8 + 4/8 = 7/8)
For 3/8 + 4/8, what equivalent fraction could allow you to move the markers on both the eighths and the halves trail? Show the moves on the Fraction Trails 1 Game Board display. (Possible response: I know 4/8 = 1/2 because the numerator 4 is half of the denominator 8. I could move 3/8 on the eighths trail and 1/2 on the halves trail.)
For 1/8 + 6/8, explain how you could move on both the eighths trail and the fourths trail. Demonstrate on the display. (I could move 1/8 on the eighths trail and change 6/8 to 3/4 to move along the fourths trail.)
How did you find the fraction equivalent to 6/8? (Possible responses: I know I have to divide the eighths in half to get fourths, so I did the same thing to the numerator. I divided the 6 in half to get 3. Or, I used the number line chart. 6/8 lines up with 3/4 on the chart.)

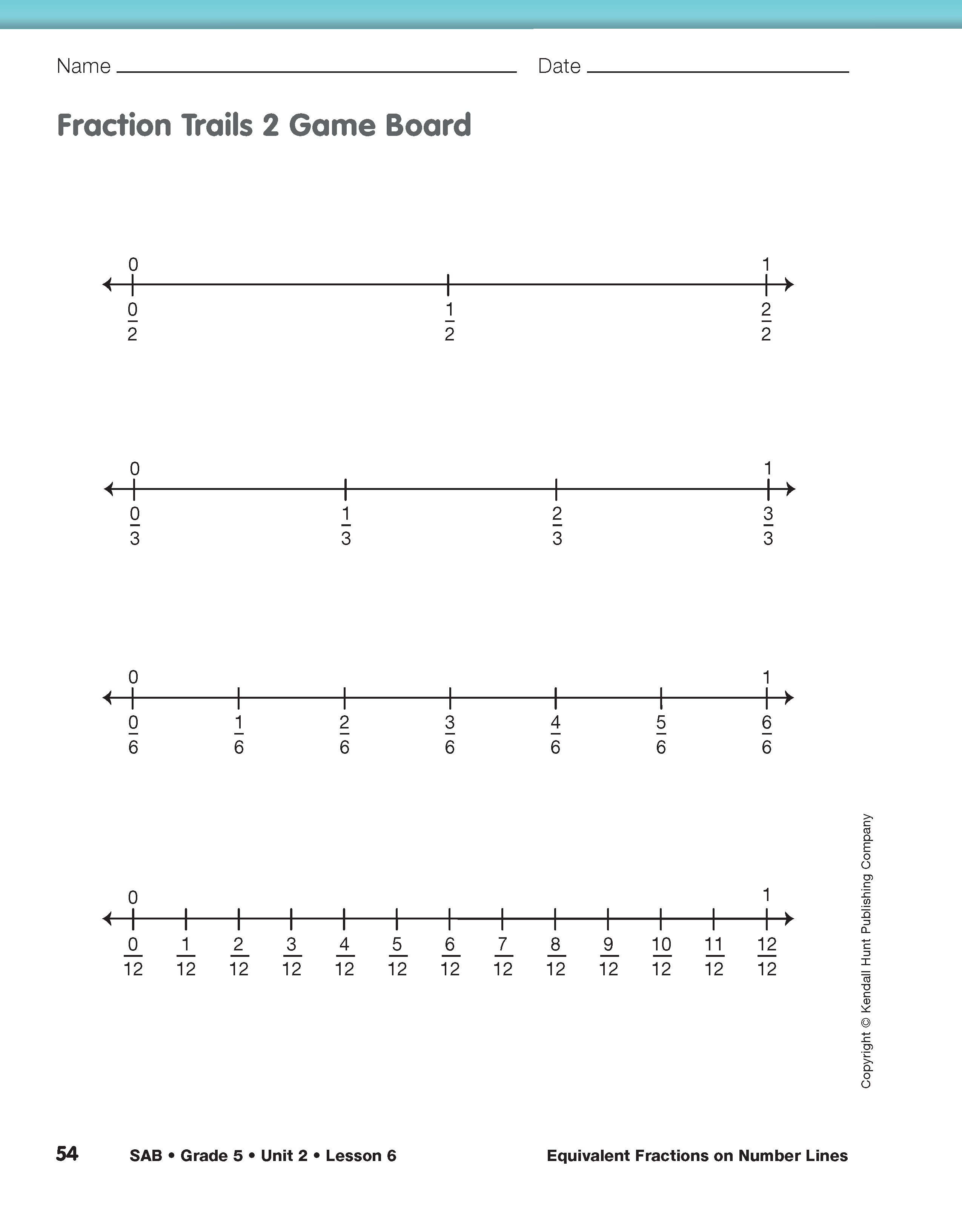
Play Fraction Trails 2 Game. Introduce Fraction Trails 2 in a similar manner. The directions are the same but halves, thirds, sixths, and twelfths are involved. Display the Fraction Trails 2 Game Board and place a marker on 1/2 , 1/3 , 1/6 , and 1/12 as shown in the example. See Figure 3. Ask students to suggest ways to move 7/12. If no one suggests a move that earns a point, demonstrate how knowing 7/12 = 1/12 + 6/12 allows a move of 1/12 on the twelfths trail and a move of 1/2 ( 1/2 = 6/12 ) on the halves number line that will earn a point. Have students play a round of Fraction Trails 2 with a partner.

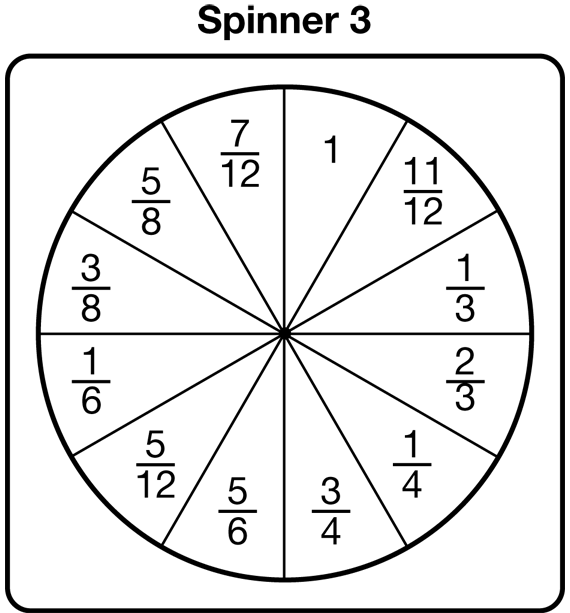
Play and Discuss Fraction Trails 3 Game. The most interesting of the games is Fraction Trails 3 because it includes all the fractions. Encourage students to play this game as soon as you think they are ready. They will use Spinner 3 on the Fraction Games Spinners pages as shown in Figure 4.

After students have played a round of the game, display the Fraction Trails 3 Game Board with markers positioned as shown in Figure 5.

Ask:

How can you move 3/4 on the Fraction Trails?
How many points will that move earn?
Is there a different way to move the same amount that will earn more points?

See the table in Figure 6 for some of the ways to move an amount equal to the fractions, and the corresponding points earned.

Have students record their responses in the form of number sentences, for example, 1/4 + 2/4 = 3/4 and 2/4 = 1/2. After you have discussed moves associated with 3/4, move the markers back to their original positions as shown in Figure 5. Repeat the process and questioning for the fractions 1/4 , 5/8 , and 7/12. Remember to make sure the markers are back in the original position before calling the next fraction.

Assign the Miguel's Fraction Trails Moves pages in the Student Activity Book for students to complete individually. Allow students to use the Fractions on Number Lines Chart page in the Student Guide Reference section.

Use the Miguel's Fraction Trails Moves pages in the Student Activity Book to assess students' abilities to find equivalent fractions using number lines and multiplication and division strategies [E4] and to decompose fractions into the sums of smaller fractions (e.g., 3/4 = 1/2 + 1/4) [E5].