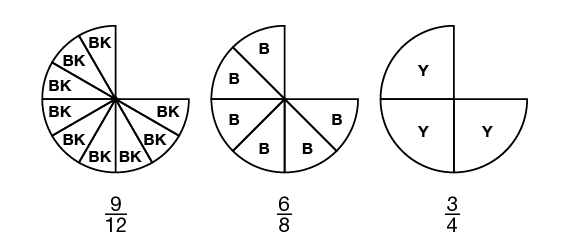
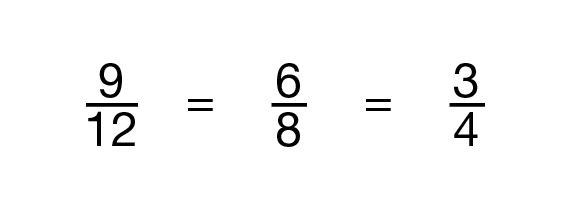Use Circle Pieces to Find Equivalent Fractions. Have students take out their fraction circle pieces and place 9 black pieces on the red circle. Show the same configuration using display fraction circle pieces.
- What fraction of the red circle is covered with black? (Responses may vary. Students will likely say 9/12 but may say 3/4.)
- What are other ways to cover the black pieces with all one color? (Use 3 yellows or 6 blues.)
- What fraction of the red circle does each of these show? (3 yellows cover 3/4 of the red circle; 6 blues cover 6/8 of the red circle.)
Have volunteers show their responses with the display fraction circle pieces. Ask students to write the fractions next to the circle pieces. See Figure 1 for possible responses.
- What do you notice about all of these models? (The same space is covered, but the space is divided into different-size pieces.)
List the equivalent fractions on the display as shown in Figure 2. Remind students that fractions with the same value are called equivalent fractions.
- Are any of these equivalent fractions simpler to use than others? If so, which one(s) and why? (Responses may vary, but students may say that 3/4, or the three yellow pieces, is easier to make sense of. They may say that they are more familiar with the size of 3/4 than they are with 6/8 or 9/12.)
Use Number Lines to Find Equivalent Fractions. Introduce students to the problem posed in Questions 1–3 of theFractions in Simplest Form pages in the Student Guide. Students read the problem and look at the map to determine the distance from Jackie's house to school in eighths of a mile. In Question 1, students locate the fraction 4/8 on the eighths number line of the Fractions on Number Lines Chart in the Student Guide Reference section. Use a display of the chart to list all the fractions equivalent to 4/8. Students then use circle pieces to show as many fractions that are equivalent to 4/8 as they can (Question 2).
- What fractions on the chart are the same distance from zero? ( 1/2, 2/4, 3/6, 4/8, 5/10, and 6/12 )
- What do you call these fractions that have the same value? (equivalent fractions)
- How did you use the chart to find the fractions equivalent to 4/8? (Possible response: I used my finger and I went up and down the chart and imagined a vertical line. Where the line hit a fraction exactly, that is an equivalent fraction.)
- Is there a fraction with 3 in the denominator that is equivalent to 4/8? How do you know? (No. There are no fractions on the “thirds” number line that line up with 4/8. Students may suggest that 4/8 can be written as
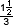 or 1.5/3. While this is not the way fractions are typically written at the fifth-grade level, it is acceptable and shows understanding of equivalence of fractions. See the Sample Dialog.)
or 1.5/3. While this is not the way fractions are typically written at the fifth-grade level, it is acceptable and shows understanding of equivalence of fractions. See the Sample Dialog.)
- How many blue pieces show the distance from Jackie's house to school if the red circle is one mile? (4 blues, since each blue piece shows 1/8 of a mile and the distance is 4/8 of a mile)
- What other pieces of a single color can you use to cover the same area as 4 blues? (1 pink, 2 yellows, 3 aquas, 5 purples, or 6 blacks)
- What fractions of a red circle, or 1 mile, do these pieces show? (1 pink is 1/2 mile; 2 yellows are 2/4 of a mile; 3 aquas are 3/6 of a mile; 5 purples are 5/10 of a mile; and 6 blacks are 6/12 of a mile.)

Use this Sample Dialog to discuss strategies for finding equivalent fractions in Question 3 in the Student Guide.
Teacher: What are some other fractions that are equivalent to 4/8 that couldn't be shown with circle pieces?
Tanya: How about 10/20?
Teacher: Okay. Why couldn't we show that with circle pieces?
Tanya: We don't have a piece that's cut into 20ths.
Teacher: That's right, we don't. So how do you know that 10/20 is equivalent to 4/8 if you can't use the circle pieces to show it?
Tanya: Well, 4/8 is the same as 1/2 because 4 is half of 8. I know 10 is half of 20, so it's the same too.
Teacher: Did anyone think of a different equivalent fraction?
Luis: How about 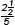 or 2.5/5?
or 2.5/5?
Teacher: Can you explain your thinking?
Luis: Tanya said the top always has to be half of the bottom. So if the bottom is 5, the top should be half of that. That's 21/2.
Teacher: Does everyone agree with Luis's fraction?
Irma: No. You can't put 21/2 on top. That's like putting a fraction in another fraction. You can't do that.
Teacher: But do you think the value of Luis's fraction is 1/2 if you could write a fraction that way?
Irma: Well, I guess so.
Teacher: It is a little unusual to write a fraction that way, but sometimes it makes sense to think of fractions like that. Did anyone use a different way to find an equivalent fraction?
Frank: I used doubles.
Teacher: Can you explain how you used doubles?
Frank: I started with 4/8. Then I doubled the top and got 8 on top. Then I doubled the bottom and got 16 on the bottom. So the fraction is 8/16.
Teacher: And how do you know that 8/16 is the same as 4/8?
Frank: Because it worked for the other fractions we found before. If you double the top and bottom of 1/2, you get 2/4, and that's the same. If you double the top and bottom of that, you get 4/8, and that's the same too. So it works every time.
Extend Representations. Have students show these fractions using fraction circle pieces. Ask them to draw the circle pieces and write a fraction for each. List all the fractions on the display.
In Question 3, students think of other fractions that are equivalent to 1/2 that cannot be shown with a single color of circle pieces. If the red circle represents the unit whole (1 mile for this problem), then only fractions with 2, 3, 4, 5, 6, 8, 10, or 12 in the denominator can be shown. No other fractions can be shown since there are no circle pieces to represent those denominators (Question 3B). At this point, students may use a variety of strategies to find other fractions equivalent to 1/2. Allow students to explore and invent methods before presenting the formal procedure discussed in the subsequent pages of the Student Guide. Students' informal strategies may resemble those in the Sample Dialog.
Finding Simplest Form. Read with the class the vignette on equivalent fractions and the simplest form of fractions. This vignette reviews a method for finding equivalent fractions that was introduced in Unit 2. Using this method, students find equivalent fractions by multiplying or dividing the numerator and denominator by the same number.
Students are introduced to the meaning of the simplest form of a fraction. Allow students to use their own reasoning to justify their answers. Students may refer to their circle pieces, number lines, intuition, or a previously learned method for simplifying fractions to justify their answers. A numerical method for simplifying fractions is discussed in subsequent Student Guide pages.
In Question 4, students find the simplest form of 4/8. While students may be able to easily identify 1/2 as the simplest form of 4/8, Question 4B asks them to justify their reasoning, which may be a more challenging task. See the Meeting Individual Needs box.

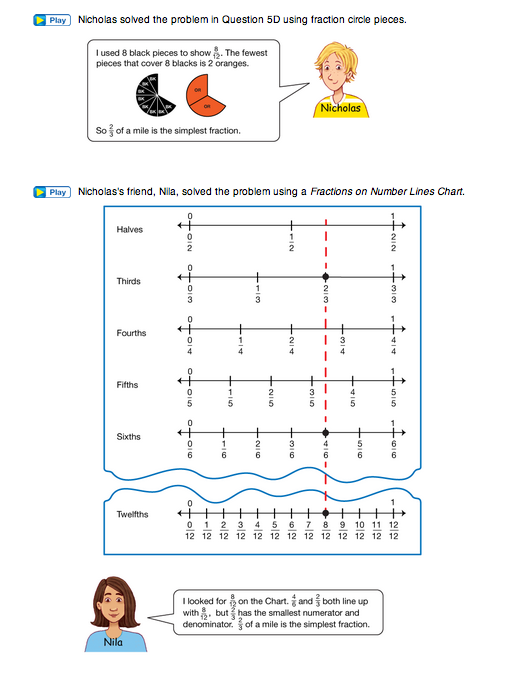
If students are having difficulty answering Question 4B or solving the problems in Question 5, you may wish to read through Nicholas's, Nila's, and Jacob's strategies shown in the Student Guide together with them. After reading Nicholas's strategy, ask:
- Do 2 orange pieces cover 8 black pieces exactly? How do you know? (Yes. Students can verify with circle pieces.)
- What fraction of the red circle is covered by 2 oranges? How do you know? ( 2/3; 1 orange is 1/3 of the red, since it takes 3 oranges to cover the red; therefore, 2 oranges is 2/3 of the red.)
- Is it possible to use fewer than 2 pieces of a single color to cover 8 black pieces? (No. The only pieces larger than the orange pieces are the pink and the red, but neither of these covers 8 blacks evenly.)
- Is 2/3 the simplest fraction for 8/12? (Yes. Based on the answer to the question above, it has the smallest possible numerator.)
After reading Nila's strategy, ask:
- How do you know all the fractions Nila marked on her number line chart are equivalent? (They all line up vertically, so they have the same value.)
- Why does Nila think that 2/3 is the simplest form of 8/12? (Of all the equivalent fractions, 2/3 has the smallest numerator and denominator.)
After reading Jacob's strategy, ask:
- How does Jacob decide to reduce 8/12? (He divides the top and bottom by 2, then by 2 again.)
- When does Jacob realize he has found the simplest fraction? (He is done when there are no common factors left to divide the top and bottom by. There are no other numbers that divide 2 and 3 evenly.)
- Are there any common factors (other than 1) that 2 and 3 share? (No. Both 2 and 3 are prime numbers, so they share no common factors other than 1.)
- What are all the factors of the numerator of 8/12? (1, 2, 4, and 8)
- What are all the factors of the denominator? (1, 2, 3, 4, 6, and 12)
- Do the numerator and denominator of 8/12 share any common factors other than 1 and 2? (yes; 4)
- How could Jacob have used this common factor to simplify 8/12 a different way? (Divide the top and bottom of 8/12 by 4.)
Have students answer Questions 5–9 with a partner. In Question 5, students solve another problem involving distance. They find equivalent fractions, first using circle pieces (Question 5A and 5B), then without using circle pieces (Question 5C). To solve Question 5C, they multiply or divide the numerator and denominator by the same number. In Question 5D, students find the simplest form of the fraction. Students should be able to justify their answers.
The next vignette shows three possible methods for finding the simplest form of the fraction in Question 5: one using circle pieces, one using the Fractions on Number Lines Chart, and one using a more formal procedure.
In Question 6, students find the simplest form of fractions by any method they choose. They are asked to show their reasoning using the strategies that Nicholas, Nila, and Jacob demonstrated in the previous vignette. Question 7 pushes students to simplify fractions using common factors larger than 2. While dividing the numerator and denominator by small numbers such as 2 is often effective, it can be more efficient to find larger common factors when possible.












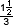 or
or 
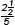 or
or