Distance vs. Time

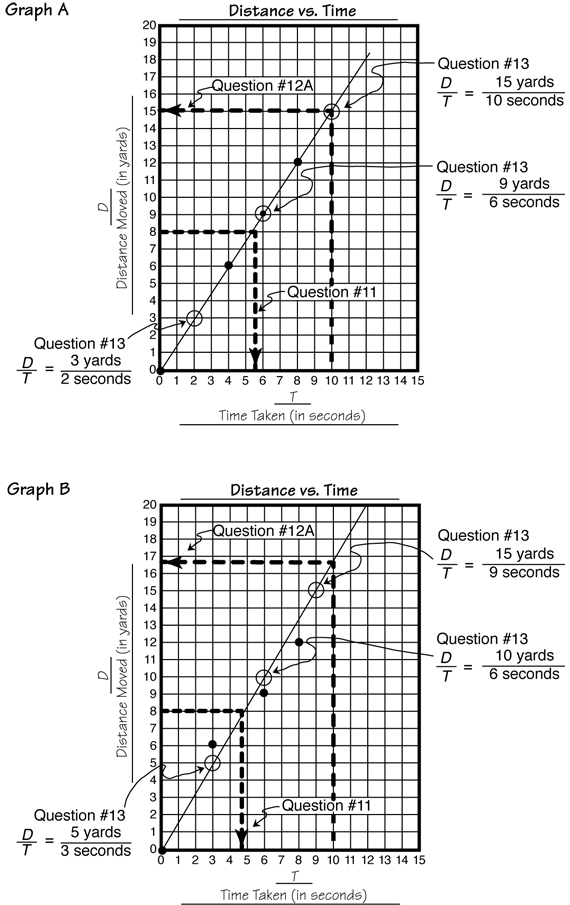
Interpret the Data. Ask students to complete Questions 11–12A using their graph. See Graphs A and B in Figure 2. Note that the graphs give slightly different answers.

Once most students have answered Question 12A, discuss Question 12B.

Next discuss Question 13. In this question, students choose a point from the graph and write the walker's speed as a ratio of distance to time (D/T) and then write two more equal ratios as fractions. The three points used to write the ratios are circled on each graph in Figure 2. They are written below as fractions:

Graph A: D/T = 3 yards/2 seconds = 9 yards/6 seconds = 15 yards/10 seconds

Graph B: D/T = 5 yards/3 seconds = 10 yards/6 seconds = 15 yards/9 seconds

Since the line goes through (0 seconds, 0 yards), the three ratios should be equal. There may be some error due to inaccuracies in estimating the values of the coordinates when reading the graph. However, all three ratios should be very close. If not, check to see that the line goes through (0 seconds, 0 yards) and students choose points on intersections to find the ratio.

Solve Problems with Data and Ratios. Ask students to work with a partner to solve Questions 14–18. Give student pairs a sheet of chart paper or drawing paper to show their work on Question 16. If students used the graph or table, ask them to attach their graph and to use dashed lines to show how it was used. Ask students to use the Math Practices page in the Reference section as a guide as they show their work. As students complete their work, display it around the room. Students who are done early should work on Questions 17 and 18.

There are multiple strategies for solving Questions 14–16. Students may use calculators to multiply and divide the large numbers involved in the problems or estimate by multiplying and dividing convenient numbers. Question 14A asks how far the walker traveled in one second. Using Graph A, we can estimate the distance traveled in one second to be 1.5 yards. Note that the ratio D/T = 3 yards/2 seconds can also be written as 1.5 yards/1 second or 1.5 yards/second (Question 14B).

Using this information, we can calculate the walker's speed in feet per second by multiplying the number of yards walked in one second by 3 (3 feet = 1 yard), so the walker's speed is 4.5 feet/second (Question 15).

One strategy for solving Question 16 is to choose a convenient ratio for the calculations. For example, using a ratio from Graph A:

9 yards/6 seconds × 10/10 = 90 yards/60 seconds

So the walker can walk 90 yards in one minute.

90 yds. × 60 min./hr. = 5400 yards in one hour or 5400 yds. × 3 ft./yd. = 16,200 feet in one hour.

Another strategy is to multiply the number of feet walked in one second by 3600 seconds (the number of seconds in one hour). The following number sentences show calculations with a calculator and with convenient numbers:

Using a calculator:
4.5 feet/second × 3600 seconds = 16,200 feet/hour

Using convenient numbers:
4 feet/second × 4000 seconds = 16,000 feet/hour

Since 4.5 is midway between 4 and 5 and 3600 is about midway between 3000 and 4000, we choose to round 4.5 down to 4 and 3600 up to 4000 so that the product is a pretty good estimate.

Since both the data and problem-solving strategies will vary from student group to student group, solutions will also vary. To determine if students calculated correctly, have them clearly describe their choices and their problem-solving processes.