Fractions and Ratios
This unit focuses on using fractions and ratios. Students find equivalent fractions and ratios, including the simplest form, to express the relationship between quantities. Ratios are represented using fractions, words, tables, and graphs. Students use ratios to describe the relationship between distance and time in an investigation about walking speed. Ratios are also used to convert between units of measure within a standard measurement system. Fraction circle pieces, number lines, and multiplication and division strategies are used to develop skills including finding equivalent fractions and ratios and finding the simplest form of a fraction or ratio.
EQUIVALENT FRACTIONS and RATIOS

Area Models
One of the key skills needed for working fluently with fractions is the ability to represent and… read more
Area Models
One of the key skills needed for working fluently with fractions is the ability to represent and identify these numbers in equivalent forms. Fraction circle pieces present a visual model for equivalent fractions. For example, by recognizing that 1 yellow piece covers the same area as 2 blue pieces or 3 black pieces, students can see the equivalence of 1/4, 2/8, and 3/12. See Figure 1. They can also see that the yellow piece is the “simplest” image of this area, and consequently, 1/4 is the simplest form of all of these fractions.
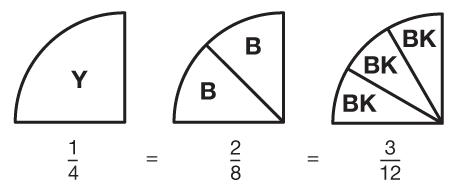
Figure 1: Equivalent fractions modeled with fraction circle pieces
Number Lines
The Fractions on Number Lines Chart provides another model for finding equivalent… read more
Number Lines
The Fractions on Number Lines Chart provides another model for finding equivalent fractions. For example, students can use the number lines to find all the fractions that are equivalent to 2/6 by finding all the fractions that “line up” with 2/6. They can see that 1/3 has the smallest possible numerator and denominator, and is, therefore, the simplest form of these equivalent fractions. See Figure 2.
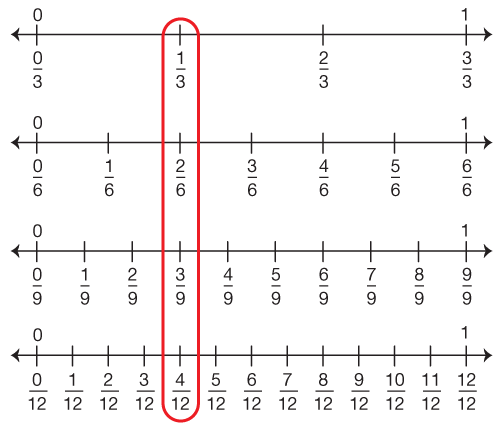
Figure 2: Equivalent fractions on number lines
Multiplication and Division Strategies
Using models to find equivalent fractions builds the conceptual understanding… read more
Multiplication and Division Strategies
Using models to find equivalent fractions builds the conceptual understanding needed before students begin to use more formalized computations for finding equivalent fractions and for simplifying fractions. Students build these procedures from their understanding of conceptual models. For example, the fact that it takes 3 black pieces to cover one yellow piece gives rise to multiplying the numerator and denominator of 1/4 by 3 to obtain the equivalent fraction 3/12. See Figure 3.
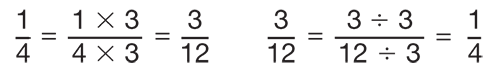
Figure 3: Using multiplication and division strategies to find equivalent fractions
RATIOS as RELATIONSHIPS BETWEEN QUANTITIES

The concept of ratio is one of the more complex topics encountered in elementary-level… read more
The concept of ratio is one of the more complex topics encountered in elementary-level mathematics. Beyond the conceptual development required to move from whole numbers to fractions, students may encounter difficulty grasping the various meanings associated with fractional quantities. Fractions, for instance, can represent parts of a whole (2/3 of a pie), a portion of a total number or individual units in a set (18/30 of all the students in the class are girls), a ratio comparing one part of a whole to another part (the ratio of girls to boys in the class is 18/12), or a comparison of two quantities that are not parts of the same whole (5 miles/2 hours). Though they are all shown the same way—a numerator over a denominator—the meanings of each are significantly different.
To this point in the Math Trailblazers curriculum, students have worked with fractions primarily as parts of a unit whole. Since this meaning of fractions is perhaps the most intuitive, it has served as the launch point for the study of fractions. Fraction circle pieces and number lines provide the primary models for developing number sense of the part-whole relationship of numerator to denominator.
In this unit, students move beyond the part-whole relationship toward an expanded use of fractions and ratios. They explore ratios such as the total cost to the number of items purchased, the number of nickels to the number of dimes of the same value, and the distance walked to the amount of time spent walking. They also use ratios to show the relationship between different units of measure within a standard measurement system. These ratios are represented using fractions, tables, graphs, and words.
The early part of this unit bridges the gap from thinking about fractions solely as parts of a whole to using fractions with this wider set of relationships. Students use fraction circle pieces to consider the number of pieces of different colors needed to cover the same area. For example, the fact that a yellow piece is 1/2 as big as a pink piece is familiar to students from their previous work with circle pieces. This part-whole relationship, however, leads to a more general ratio expressed in words: two yellow pieces are needed to cover every pink piece. See Figure 4.
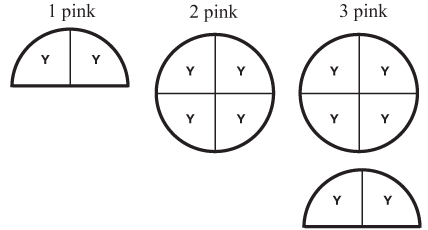
Figure 4: Modeling the ratio of the number of pink pieces to the number of yellow pieces
Based on this statement, students find the following series of equivalent ratios that describe the relationship.
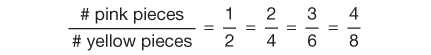
In a different context, equivalent ratios are written as fractions to represent one person's share of cookies compared to the total number of cookies that need to be shared fairly among 4 people.

While there is still a familiar connection to part-whole fractions in this context, the series of equivalent fractions shows the ratio as a fixed relationship between variable quantities. The goal is that students are able to show ratio relationships using equivalent fractions as well as tables, graph points, and verbal descriptions as shown in Figure 5. At the same time students need to understand that, although fractions occur in different situations with different meanings, the mathematical procedures for naming, comparing, and operating on fractions are the same.
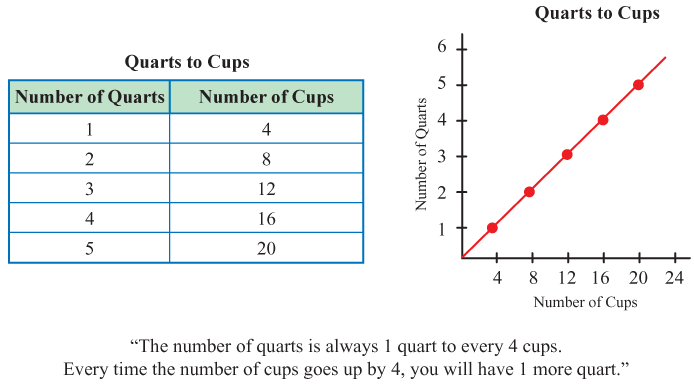
Figure 5: Representations of the ratio of quarts to cups
MATH FACTS and MENTAL MATH

This unit continues the review and assessment of the multiplication and division facts… read more
This unit continues the review and assessment of the multiplication and division facts to develop mental math strategies, gain fluency, and to learn to apply multiplication and division strategies to larger numbers. Students will focus on the multiplication and division facts for the square numbers.
Resources
- Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically. Heinemann, Portsmouth, NH, 2003.
- Carraher, D.W. and A.D. Schliemann “Early Algebra.” In Second Handbook of Research on Mathematics Teaching and Learning. F.K. Lester, Jr., ed. Information Age Publishing, Inc., Charlotte, NC, 2007.
- Cramer, K. and A. Henry. “Using Manipulative Models to Build Number Sense for Addition of Fractions.” In Making Sense of Fractions, Ratios, and Proportions, 2002 Yearbook. B. Litwiller and G. Bright, eds. National Council of Teachers of Mathematics, Reston, VA, 2002.
- Cramer, K., M. Behr, R. Lesh, and T. Post. The Rational Number Project Fraction Lessons: Level 1 and Level 2. Kendall Hunt Publishing, Dubuque, IA, 1997.
- Kaput, J.J. Algebra in the Early Grades. Lawrence Erlbaum Associates, New York, NY, 2008.
- Kilpatrick, J. and A. Izsak. “A History of Algebra in the School Curriculum.” In Algebra and Algebraic Thinking in School Mathematics. C.E. Greenes and R. Rubenstein, eds. The National of Teachers of Mathematics, 2008.
- Lamon, S. Teaching Fractions and Ratios for Understanding: Essential Content Knowledge and Instructional Strategies for Teachers, 2nd Ed. Lawrence Erlbaum Associates, Mahwah, NJ, 2005.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- Schliemann, A.D., D.W. Carraher, and B.M. Brizuela. Bringing Out the Algebraic Character of Arithmetic. Lawrence Erlbaum Associates, Mahwah, NJ, 2007.
- Van de Walle, J.A. and L. Lovin. Teaching Student Centered Mathematics: Grades 3–5. Pearson Education, Boston, 2006.











