Equivalent Fractions and Ratios

Est. Class Sessions: 3

Developing the Lesson

Part 1: Connect Fractions to Ratios

Relate Fractional Parts to Each Other. Have students work with partners, sharing two sets of fraction circle pieces.

Ask students to use their pieces to answer the following questions:

How many yellow pieces does it take to cover the red piece? (4 yellow pieces)
What fraction of the red piece is covered by one yellow piece? (1/4)
How many orange pieces does it take to cover the red piece? (3 orange pieces)
What fraction of the red piece is covered by two orange pieces? (2/3)

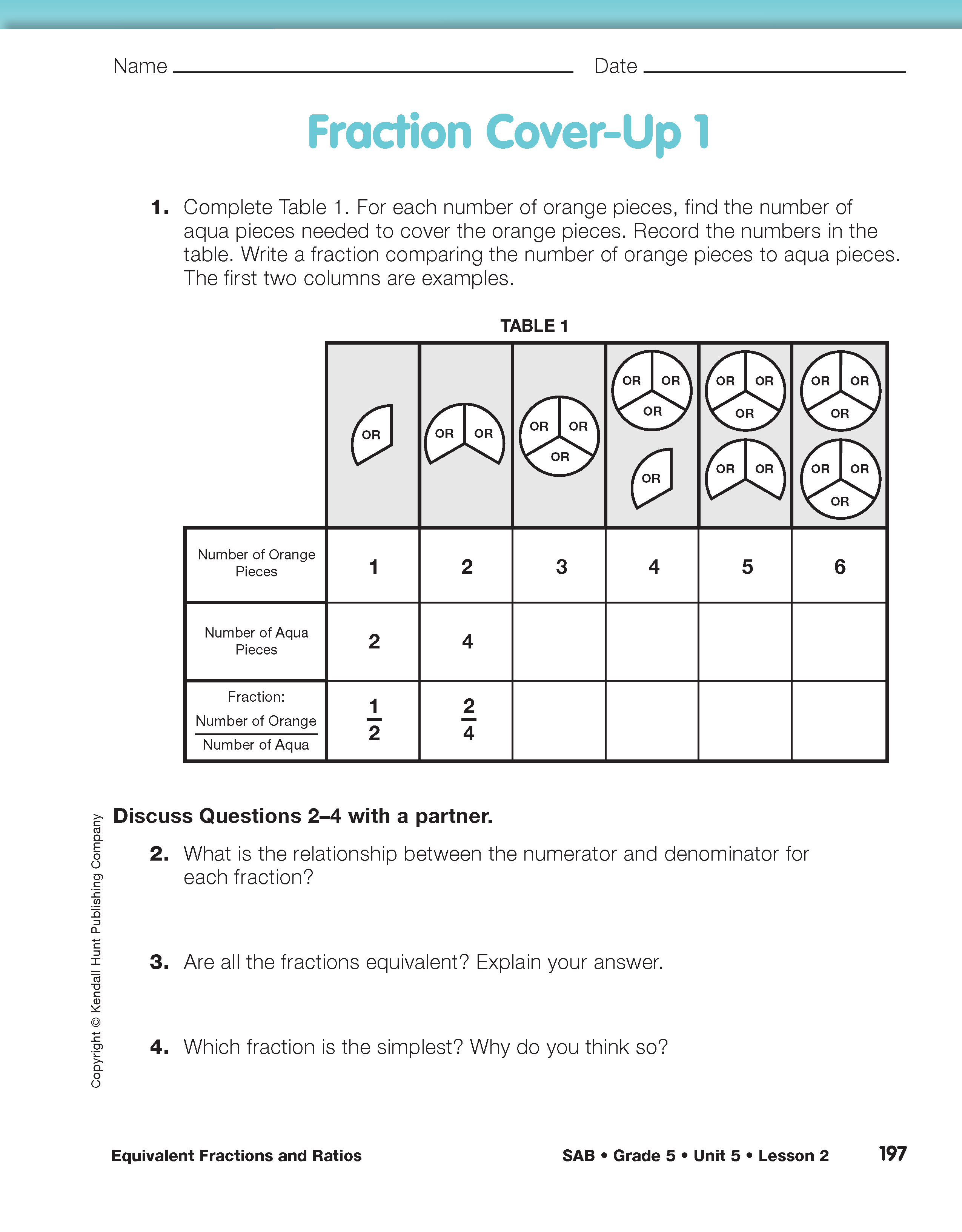
Show students Table 1 on a display of the Fraction Cover-Up 1 page in the Student Activity Book. Read the instructions with the class. For the first two columns, ask students to verify the number of aqua pieces needed to cover the given number of orange pieces.

Ask:

How many aqua pieces does it take to cover one orange piece? (2 aqua pieces)
What can you say about the area covered by one orange piece compared to two aqua pieces? (The areas covered are the same, since the shapes cover each other evenly.)
How many aqua pieces does it take to cover two orange pieces? (4 aqua pieces)
What do the fractions mean in the third row of the table? (Students may respond that the 1/2 means an aqua piece is 1/2 as big as an orange piece. This conclusion is correct, but the fraction actually describes the ratio of the number of orange pieces to aqua pieces needed to cover the same area.)

Introduce Ratios. Fractions that are not part-whole may be a new concept for some students. Explain that fractions are not always a part of a unit whole. Fractions can be used to show a ratio, or a comparison of two quantities.

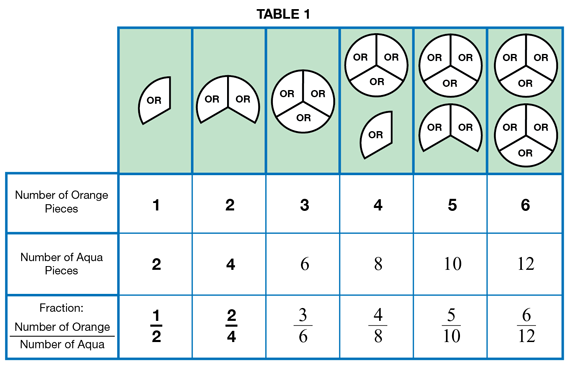
Ask students to complete Table 1 using orange and aqua circle pieces. See Figure 1 for a completed table. In this case, the ratios compare the number of orange pieces to the number of aqua pieces it takes to cover a shape. Have students discuss Questions 2–4 with a partner and then share responses with the whole class.

Ask:

What patterns do you notice in the table? (Responses may vary. Students may say that the number of orange pieces goes up by ones and the number of aqua pieces goes up by twos, that the fractions all have the same value of 1/2, or that the denominators of the fractions go up twice as fast as the numerators.)

Use Question 3 to discuss the meaning of equivalence of fractions. Ask students to justify their answers to the question by having them explain what it means for fractions to be equivalent. A more structured discussion about fraction equivalence takes place in Part 2 of this lesson.

Ask:

How do you know all the fractions in Table 1 are equivalent? (All the fractions are equal to 1/2. If you multiply the numerator and denominator by the same number, you can get all the fractions in the row. Or, for all the fractions in the row, the denominator is double the numerator.)
How is the pattern in the fractions related to the patterns in the fraction circle pieces? How do the pieces show the doubling pattern? (Possible response: One orange can be covered by two aquas, two oranges can be covered by four aquas, three oranges can be covered by six aquas, and so on. The pattern goes like that, doubling the number of aquas for each orange. The number of orange pieces is the numerator and the number of aqua pieces is the denominator, so that's why the doubling pattern is in the fractions.)

Identify Simplest Form. For Question 4, some students may interpret the word “simplest” in the formal sense of “lowest terms.” Some students may be unfamiliar with this definition and pick the fraction that looks the simplest.

Ask:

What about the fraction makes it the simplest one? (If students picked 1/2, they may say that it has the lowest numbers or that, more formally, there is no way to divide the top and bottom by the same number.)

In Questions 5–10, students write the ratio of orange pieces to aqua pieces in three different ways. Emphasize that a ratio is a way to express a comparison of two quantities.

Ask:

Which of the statements in Questions 5–10 represent ratios? (All six of them, since they all express a comparison of the number of orange pieces to aqua pieces.)
Which of the ratios are in the form of a fraction? (Questions 7–10 only. The statements in Questions 5 and 6 express a ratio but not in fractional form.)
Which ratios are in simplest form? (Questions 9 and 10)

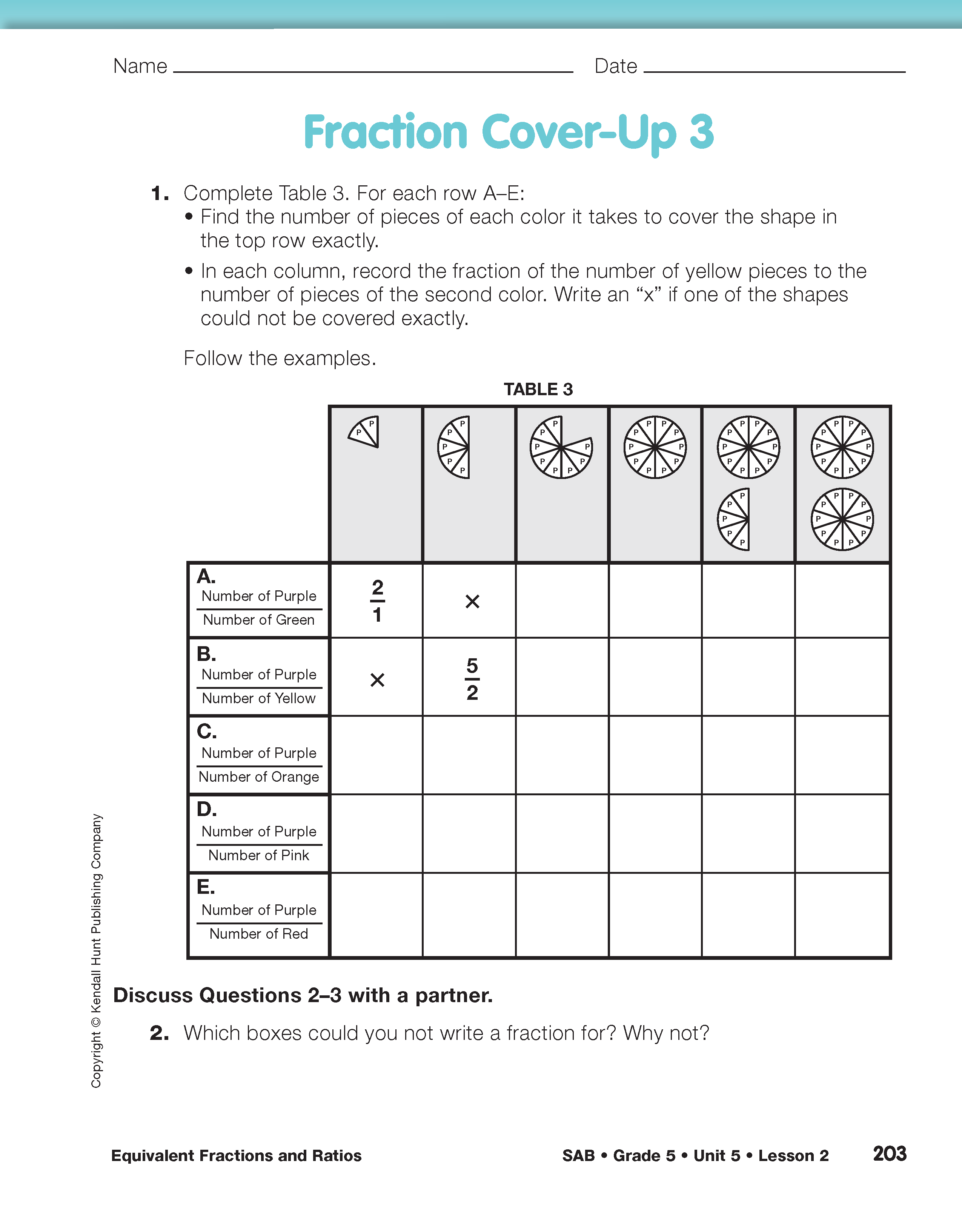
Find Equivalent Ratios. Show students Table 2 on a display of the Fraction Cover-Up 2 page in the Student Activity Book. Read the instructions with the class.

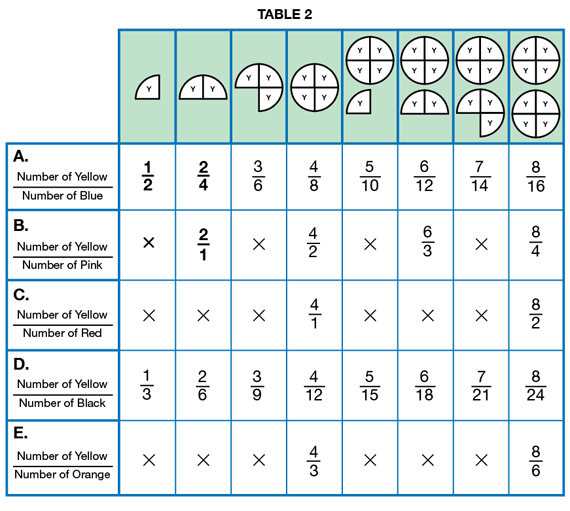
Ask students to use their fraction circle pieces to verify that the example entries in Table 2 are correct.

Ask:

Use your fraction circle pieces to cover a yellow piece with blue pieces. Can you cover the yellow piece exactly? (yes)
How many blues cover a yellow? (2 blue pieces)
Is the first fraction in Row A correct? Why or why not? (Yes, the number of yellow pieces over the number of blue pieces is 1/2.)
Is the second fraction in Row A correct? Show me with the fraction circle pieces. (Yes. Students should cover two yellow pieces with four blues. The number of yellow pieces to the number of blue pieces that it takes to cover the shape is 2/4.)
Why is there an x in the first box in Row B? (You can't cover one yellow piece with a pink piece exactly.)
Is the fraction in the second box in Row B correct? Show me with the fraction circle pieces. (2/1 is correct because it takes 2 yellow pieces and 1 pink piece to cover the shape in the gray row.)

Ask students to work with a partner to use fraction circle pieces to fill in the table. Remind students that for several of the rows there will be boxes where fractions cannot be written. For example, in the third column of Row B, a pink piece does not evenly cover three yellow pieces. Therefore, an 'X' is placed in the box. See Figure 2.

Ask student partners to discuss Questions 2–8. The discussion of patterns and equivalence of fractions may be similar to the discussion for Fraction Cover-Up 1. In Questions 4–8, students identify when fractions will be greater than one, based on the relationships between different-colored circle pieces. Have students share responses with the whole class.

In Questions 9–14, students write ratios to compare the number of pieces of different colors needed to cover the same area. In Questions 13 and 14, students write ratios that are written as a comparison of quantities with different units. Fractions of this type are different from the whole-part fractions students worked with in Unit 2. See the Content Note.

What is the difference between a ratio and a fraction? Since these words are often used interchangeably, it is important to note how ratios and fractions are the same and how they are different. A ratio is a comparison of two quantities. It can be written as a fraction, such as 1/4. Ratios can also be written as 1:4 (read “one to four”) or with words, such as “1 unit for every 4 units.” A fraction is a specific way to write a ratio with one quantity (the numerator) written above the other quantity (the denominator).

Different meanings of fractions. Fractions are commonly used to show part-whole relationships, such as 1/8 of a pizza, which represents 1 part of 8 equal pieces that make up a unit whole. Fractions can also show part-part relationships, such as 5 girls/4 boys, where both the numerator and denominator are parts that make up a whole group of 9 children. Fractions also describe relationships between different types of quantities. For example, a fraction can describe the speed of a person who walks 5 miles in 2 hours. The speed is written as the fraction 5 miles/2 hours. In this case, the fraction line is read as “per” or “for every.” The number and the units are typically separated as 5 mi./2 hr. ( 21/2 mi./hr. or 2.5 mi./hr.).

Use Decimals to Describe Fractions and Ratios. Fraction Cover-Up 3 in the Student Activity Book provides practice for students in using decimals to describe fractional equivalents and ratios. By using the red circle as the whole, students explore the relationship of the purple pieces (tenths) to the pink pieces (halves), the orange pieces (thirds), the yellow pieces (fourths) and the green pieces (fifths).

Use of the fraction circle pieces representing fifths and tenths helps build the students' number sense of decimals to the tenths place.

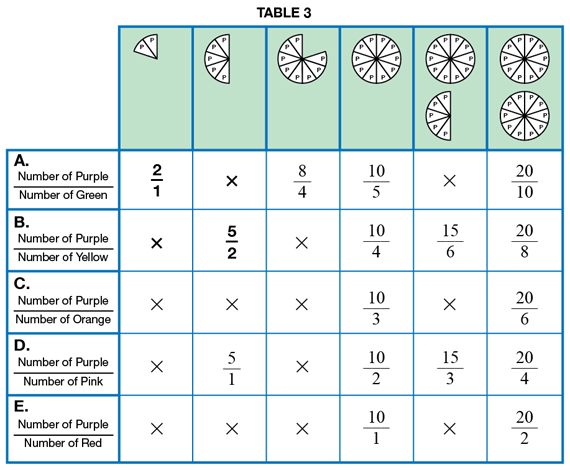
Show students a display of Table 3 in the Student Activity Book. See Figure 3. Read the instructions with the class.

Ask students to use their fraction circle pieces to verify that the example entries (bolded) in Table 3 of Fraction Cover-Up 3 are correct.

Ask:

Use your fraction circle pieces to cover two purple pieces with a green piece. Can you cover the two purple pieces exactly? (yes) Can you cover the two purple pieces exactly with yellow? (no)
Use your fraction circle pieces to cover 5 purples. Can you cover five purple pieces exactly with yellow pieces? (yes) How many yellows? (2) Can you cover five purple pieces exactly with green pieces? (No. No number of greens will cover 5 purples exactly.)
In this activity the red circle represents the unit whole. What fraction of the red circle do five purple pieces cover? (one-half) How do you write this as a decimal fraction? (.5)

Have students work with partners, sharing two sets of fraction circle pieces. Ask students to complete Table 3 in Fraction Cover-Up 3. Have students discuss Questions 2 and 3 with a partner. Walk around the room to listen to their discussions and see how students figure out different ways to represent the decimal fractions with the fraction circle pieces.

Bring the class back together to explore Question 3A. Use a display and demonstrate or have two students demonstrate how to represent the decimal fraction 1.2 with the fraction circle pieces in more than one way. In at least one example, include the purple pieces to strengthen the students' use of tenths and the green pieces to strengthen their use of fifths. Students should be able to articulate that .2 is two-tenths (11/12) and understand that its equivalent and simplest common fraction is one fifth (1/5). Have students share their answers to Question 3B using the display.

After the class discussion, students work independently using Table 3 and the fraction circle pieces to answer Questions 4–12. These questions strengthen students' visualization of tenths expressed as decimal or common fractions and guide students in uncovering how the value of the ratio depends on whether the red piece is compared to the purple piece or the purple piece is compared to the red piece.

In Questions 11A–C, students explore the relationship between one red circle piece and 1 purple piece. Students should recognize that since it takes 10 purple pieces to cover the red circle, one tenth of the red circle is equal to 1 purple piece. To express this relationship in words, students can write one-tenth of a red piece is equal to one purple piece. For Question 11B, students express this ratio using a common fraction. Since the ratio is showing the relationship between the red piece and one purple piece, the ratio is expressed as 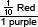. In Question 11C, students express this ratio by expressing 1/10 using decimal notation (.1) in the numerator.

If students are confused by this, use these or similar prompts to increase student understanding.

Ask:

What two things are being compared in this ratio? (Possible response: The red piece is being compared to the purple piece.)
When you write a ratio as a fraction, what does the numerator tell you? (Possible response: It tells you the value of one of the things you are comparing.)
What does the denominator tell you? (Possible response: It tells you the value of the second thing you are comparing.)
What is the value of the red piece that is equal to one purple piece? (one-tenth)
Where do you write that in this ratio? (as the numerator)
What is the value of the purple piece in this ratio? (It is one, or the whole.)
Where do you write that in this ratio? (as the denominator.)
How can you use a decimal to express the 1/10 in the numerator? (.1)
How can you express the ratio of the red piece to one purple piece using this decimal notation? (.1/1)