Using Ratios

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Representing Ratios

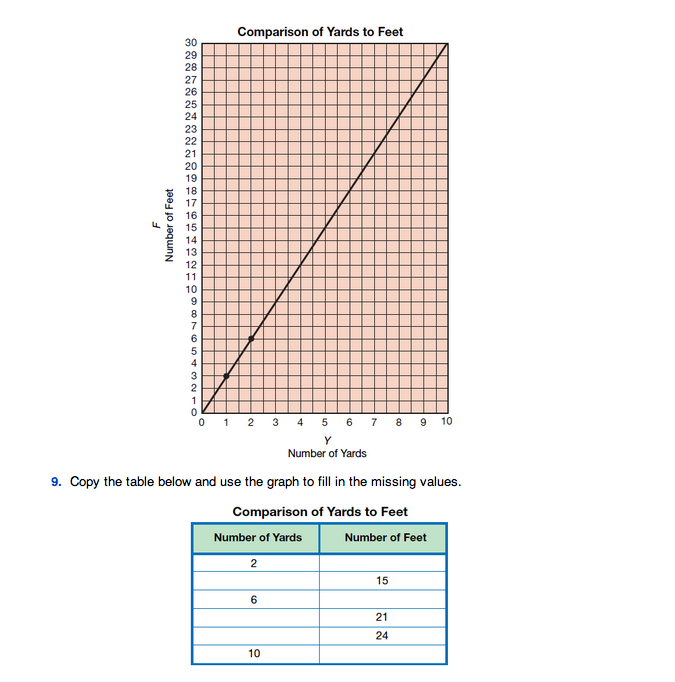
In the Ratios section in the Student Guide, students use words and symbols to express ratios and to show equivalence between ratios. In Question 8 they use words to name ratios equal to “2 cookies for 25¢” and in Questions 9–12, they use a graph to find ratios equal to 3 feet/1 yard and write them as fractions. In Questions 13–14, students use that ratio to solve related problems.

Display the Using Ratios to Convert Between Yards and Feet Master and show students how to use the graph to convert feet to yards and yards to feet and how to write equal ratios using points on the line. Ask students to solve each question by reasoning and using the graph.

It is important that students make connections between the various representations of ratios (words, tables, graphs, and symbols), so that they can use them as tools to solve problems. Equal ratios can be shown as entries in a table, points on a straight line which goes through (0,0), and equivalent fractions. Question 15 helps students see these connections. They must decide if 25¢/2 cookies is equal to 15¢/1 cookie (Question 15A). It should be clear to students that the fractions are not equivalent (25¢/2 cookies ≠ 15¢/1 cookie) since doubling the number of cookies does not double the cost. Question 15B asks students to add a point for the ratio 15¢/1 cookie to the graph they made in Question 5. See Figure 3. This point does not lie on the line since the line is made up of points with ratios equivalent to 25¢/2 cookies. This is an example of the general principle that points will lie on the same line through (0,0) only when the ratios are equal.

Proportions. A proportion is a statement of equality between two ratios. Although the term proportion will be introduced in a later unit, students use proportional reasoning throughout this lesson. Proportional reasoning is an important theme across the Math Trailblazers curriculum, especially in the third, fourth, and fifth grades. Students encounter proportions in many representations: concrete materials, real-life situations, tables, graphs, and symbols. They make connections between these representations and use them as tools to solve problems that require proportional thinking.