Workshop: Using Equivalent Fractions and Ratios

Est. Class Sessions: 1–2

Developing the Lesson

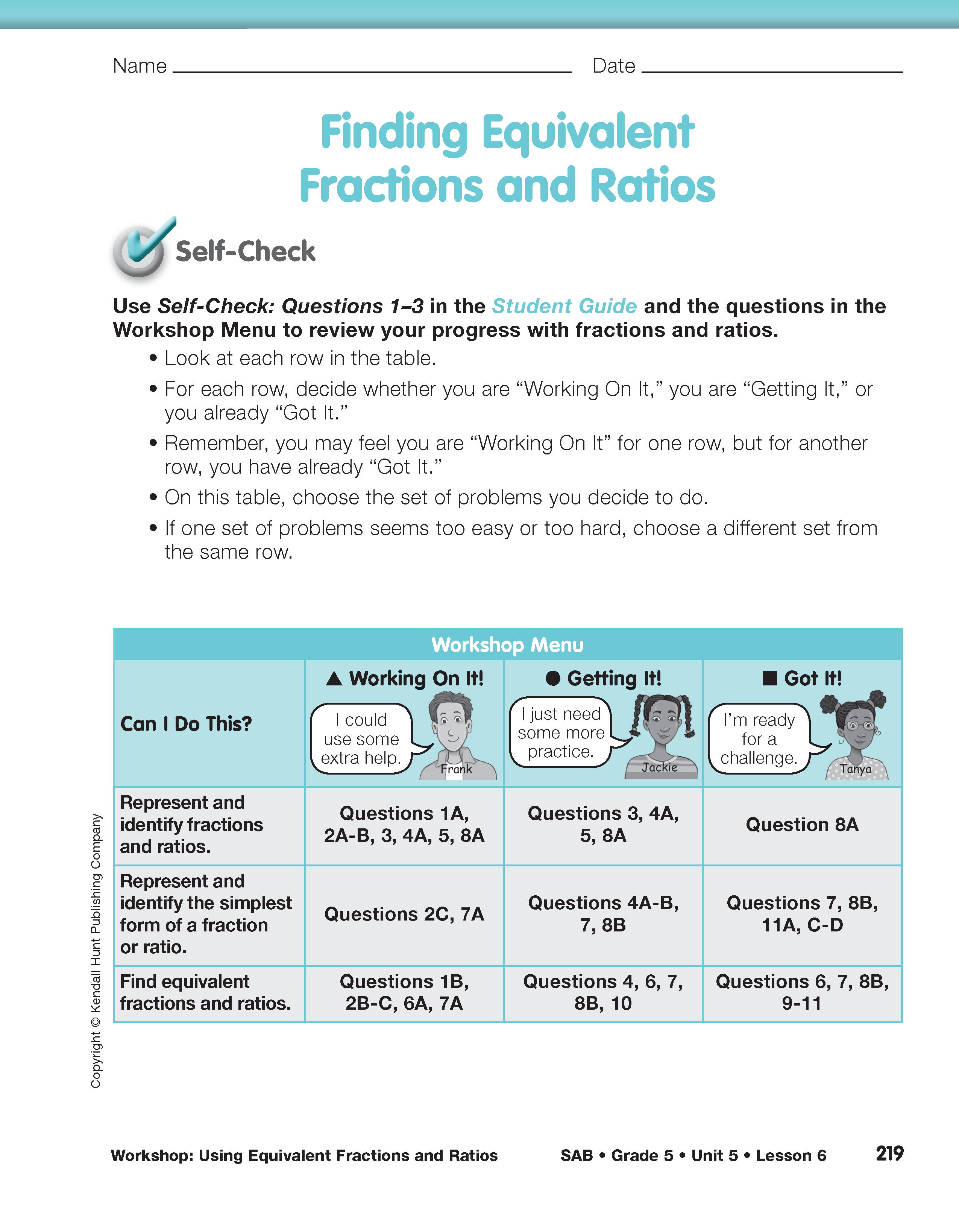
Set Up the Workshop. Direct students to the Workshop: Using Equivalent Fractions and Ratios pages in the Student Guide. These pages contain the Self-Check Questions for this Workshop. Students begin by completing Self-Check: Questions 1–3 either individually or with a partner. These questions serve two purposes. First, they clearly communicate the content of the related targeted practice to the students. Second, they help students quickly assess their progress with the Expectations to help them choose which problems to work on in the Workshop.

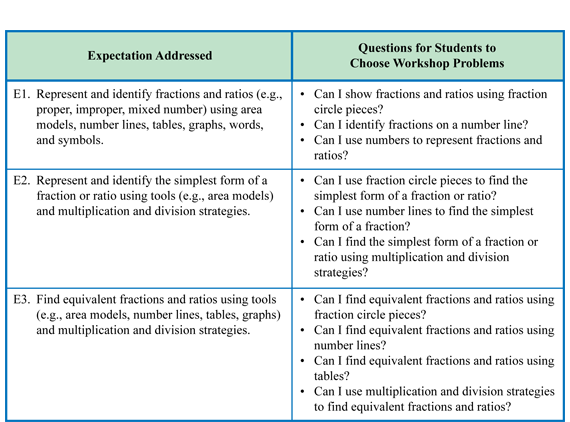
Use Self-Check: Questions 1–3 in the Student Guide to assess students' abilities to represent and identify fractions and ratios (e.g., proper, improper, mixed number) using area models, number lines, tables, graphs, words, and symbols [E1]; represent and identify the simplest form of a fraction or ratio using tools (e.g., area models) and multiplication and division strategies [E2]; and find equivalent fractions and ratios using tools (e.g., area models, number lines, tables, graphs) and multiplication and division strategies [E3].

Choose Targeted Practice. After students have completed Self-Check: Questions 1–3, discuss each question with the whole class. Ask students to share their solutions and explain their reasoning using the display set of fraction circle pieces and the display of the Fractions on Number Lines Chart in the Student Guide Reference section as needed. Facilitate a class discussion of students' solutions. Next have students think about each “Can I Do This?” question in the menu in the Student Activity Book. Ask students to review their work to decide which problems to choose from the following groups:

Students who are “working on it” and need some extra help should circle the problem set marked with a triangle (). These problems provide scaffolded support for developing the essential underlying concepts as well as some opportunities for practice.
Students who are “getting it” and just need more practice should circle the problem set marked with a circle (). These problems provide opportunities to practice with some concept reinforcement and some opportunities for extension.
Students who have “got it” and are ready for a challenge or extension should circle problems marked with a square (). These problems provide some practice and then move into opportunities for extension.

Check students' choices to see how well they match your own assessment of their progress on the related Expectations. Help students make selections that will provide the kind of practice they need. Figure 1 shows the Expectations for this Workshop and provides questions to help students decide what practice they need.

Note that students' self-assessment of their own abilities may vary between rows in a menu or between menus. For example, a student might circle the “” questions in one row and the “” or “” questions in another row or in a subsequent menu. A student's comfort and ability may vary by Expectation, and the Workshop allows each student to choose problems flexibly based on what type of practice he or she needs for each “Can I Do This?” question.

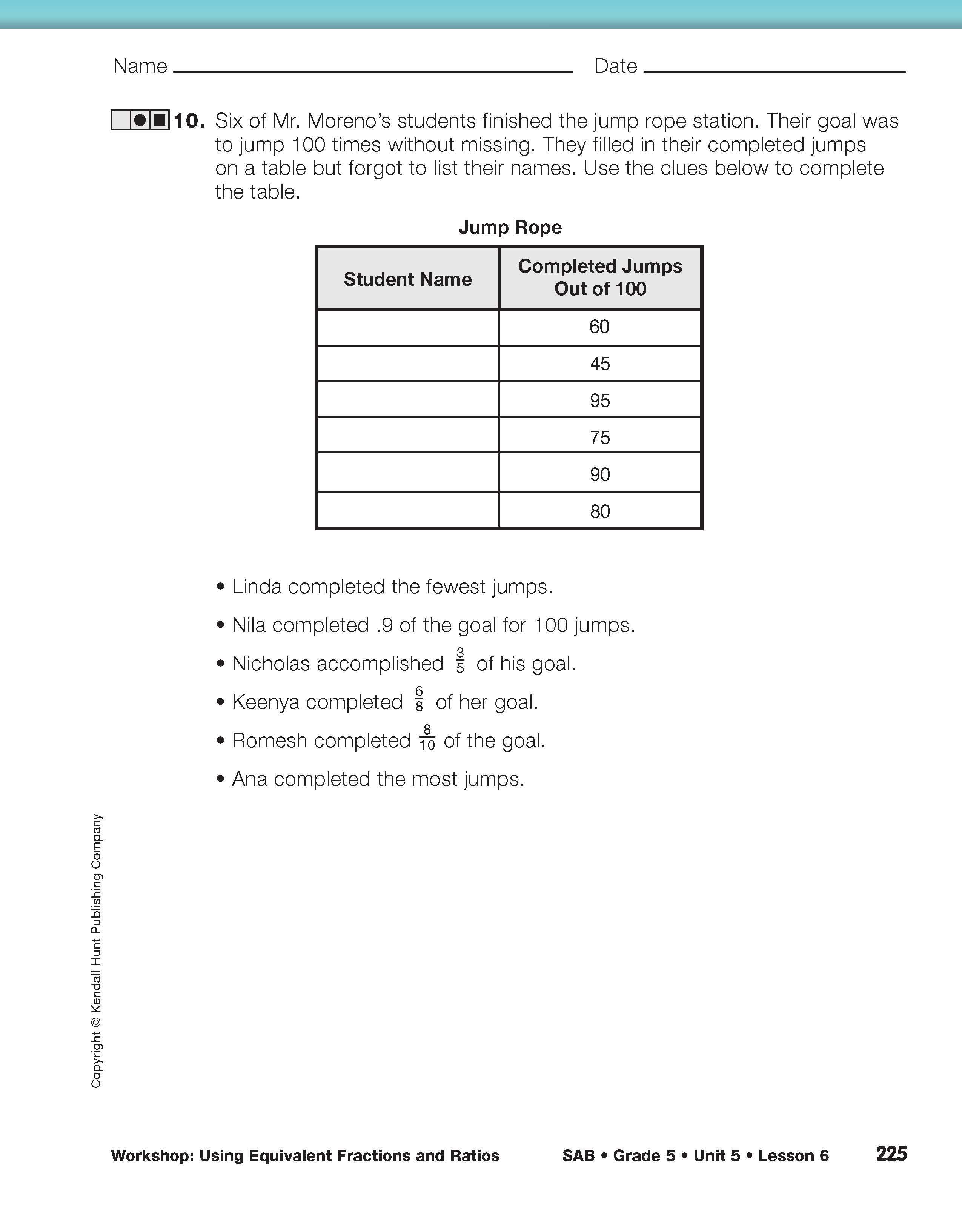
Once students select the questions to complete in the Workshop, match groups of students who have chosen similar sets of problems from the menu. Have students work together with a partner or in a small group to solve the problems they chose. The problems for this workshop are in the Student Activity Book on the Finding Equivalent Fractions and Ratios pages.

There are many ways to vary a lesson to meet a wide variety of student needs. One way is to allow students to use different tools and processes. Some students will need to depend on the concrete models of fraction circle pieces, number lines, and pictures; others can use these models more efficiently; and still others may be ready to let go of the concrete models.

Encourage students to use fraction circle pieces, refer to the Fractions on Number Lines Chart page in the Student Guide Reference section, draw pictures, and sketch number lines to support their solutions.
Some students will use invented strategies. Encourage these students to use more than one strategy to solve a problem and compare their solutions.
Some students may be able to use only symbolic models. Encourage these students to use the concrete models to check their solutions when appropriate, and ask them questions to ensure that they make connections between the models and the symbols. Continuing to use the concrete models gives students experiences that build number sense, estimation skills, and flexibility. To encourage deeper understanding of the concepts, ask students to solve a problem another way or to show another representation of the problem.

Before students begin work, direct them to the Math Practices page in the Student Guide Reference section.

Ask students to review Math Practices Expectations E1, E2, E5, and E6 with a partner before asking:

As you are working on the problems in the workshop, what are some of the ways you can make sure you understand what the problem is asking? (Possible response: You need to read each question carefully and think about the question it is asking you to answer. You need to think about what the numbers mean in each problem and you need to think about the units or labels for each question.)
What strategies or tools can you use to solve each problem? (Possible response: You can use tools like fraction circle pieces or the Fractions on Number Lines Chart. You can also draw pictures or use the patterns that you see to solve problems. You can use multiplication and division to solve some problems.)
Some problems will ask you to explain your thinking or show how you found your solution. What are some of the things you should include in an explanation so other people know what you are thinking? (Possible response: You can explain your thinking using words to explain each step you took and the tools or strategies you used to solve the problem. You can include drawings to help show your thinking. You should include labels to tell what the numbers mean.)
Why is it important to include labels when you are expressing ratios? (Possible response: Since ratios tell the relationship between two different things, you need to label each part of the ratio so people can clearly see the relationship.)

Share Workshop Experience. After students have had time to work on their selected problems, choose a few problems from the Workshop to discuss as a class. You might choose these problems to represent common areas of difficulty for students or areas where students made significant progress over the course of the unit. You may also choose to discuss problems that all or most students would have solved. Questions 6A, 7A, and 8A in the Student Activity Book should have been completed by all students.

Some students may not have completed all of their questions before you discuss selected questions with the whole class. While this may mean interrupting students' flow of work, it is also important that students have an opportunity to share their solution strategies. For students who need more time, unfinished problems can be completed at the end of the Workshop lesson as needed. They can also be sent home as homework.

Student Guide: 238 239

Answers