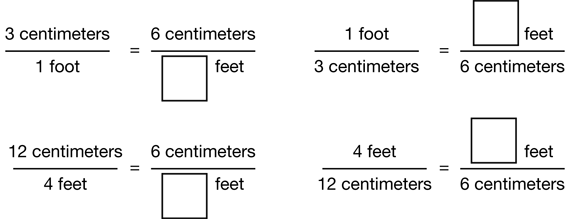Lesson 5

Problems of Scale

Est. Class Sessions: 1–2

Developing the Lesson

Part 2. Use Ratios to Solve Problems of Scale

Direct students to the Problems of Scale pages in the Student Guide. Read the opening vignette with students.

Ask:

X
  • What are some other scale models that you are familiar with? (Possible responses: models of vehicles including cars, boats, planes, helicopters, trains; doll house models, building kits, etc.)
  • What are some other places where you have seen scales used to represent measurements? (Possible responses: on maps and globes, in drawings, or in directions for putting an object together)
  • What are some reasons why it is important to be able to represent distances using a map scale? (Possible responses: When you travel you may need a map so you can tell how far you need to go on each road. You would not know any of the actual distances if you did not have a scale. Airlines need to know the exact distances between airports so they can decide how much fuel they need and the time it will take to travel between destinations.)
  • What are some uses for scale drawings? (Possible response: Architects and builders use scale drawings to plan buildings and to decide how much space and building materials they will need. When you buy something that needs to be assembled there are usually scale drawings included to show you how you need to put the object together.)

Direct students to work with a partner and complete Questions 1A–B. These questions provide an opportunity to quickly review strategies for finding equivalent ratios. Ask several students to share their strategies with the class.

In Question 1A, students should see that there is a multiplicative relationship of times 4 between the numerator of 3 in the first ratio and the numerator of 12 in the second ratio. They can use this relationship to find the denominator in the second ratio (the length of the actual windows) by multiplying 1 foot × 4 = 4 feet. Students should also see that since every 3 cm represents 1 foot, if they divide 12 cm by 3 cm they will know how many feet are represented by 12 cm. 12 cm ÷ 3 cm = 4, so each window is 4 feet long in an actual house. Since this is a scale model, students can use different equivalent ratios to find that the width of an actual window will be 2 feet, for Question 1B.

See Figure 2 for possible solutions.

Student Guide: 236
Answers
X
SG_Mini
+
Student Activity Book:
Master:
Four possible number sentences using equivalent ratios to find the width of each window
X
+