Equivalent Fractions and Ratios

Est. Class Sessions: 3

Developing the Lesson

Part 2: Finding Equivalent Ratios

Read the opening vignette in the Equivalent Fractions and Ratios pages in the Student Guide with the class.

Ask:

Last week, how many cookies did Grace's grandmother bring? (4 cookies)
How many cookies did Grace get? (1 cookie)
What fraction of the total cookies did Grace get? (1/2 of the cookies)
What number is the numerator? What does it represent? (The numerator is 1. It is the part Grace gets.)
What number is the denominator? What does it represent? (The denominator is 4. It is the total number of cookies, or the “unit whole.”)
What fraction of the total cookies does Grace get this week? (Student responses may vary. Students may say Grace gets 2/8 of the cookies. They may also say that she still gets 1/4 if they recognize 1/4 and 2/8 as equivalent fractions.)

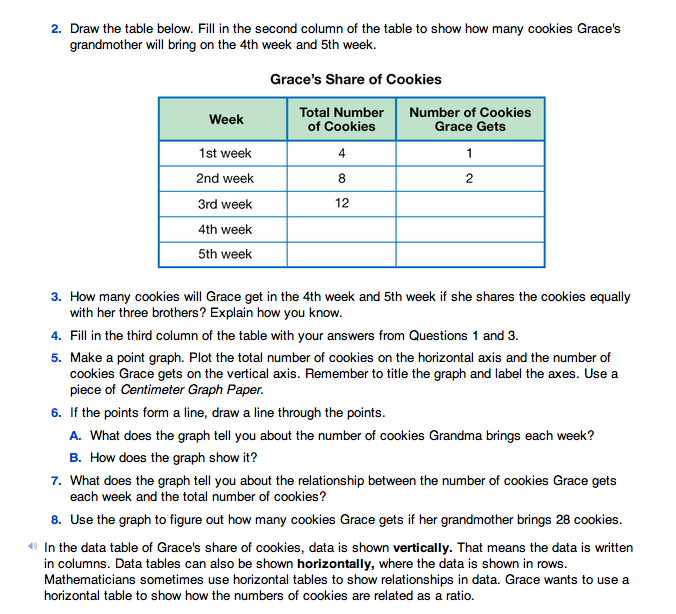
Students discuss Questions 1–4 in small groups. Students can continue a pattern of repeated addition to complete the second column of the table “Grace's Share of Cookies.” They can use patterns or simple division to compute Grace's share in the third column of the table. In Questions 5–6, students make a point graph of the data in the table and draw a line through the points. They use the graph to make predictions about the relationship of Grace's share to the total number of cookies in Questions 7–8.

In Question 9, students re-write the table horizontally instead of vertically. This helps students make the visual connection between the data table and the fractional relationship between Grace's share of cookies and the total cookies in Question 10. For Questions 11–14, students write the data points as fractions and look for patterns. In Questions 13–14, they show the difference between equivalence of whole-number quantities and equivalence of fractions. The number of cookies Grace gets increases each week, whereas the fraction of the total she gets remains the same because the numerator and denominator are both increasing by the same ratio. This is an important aspect of fractions to be emphasized with students.

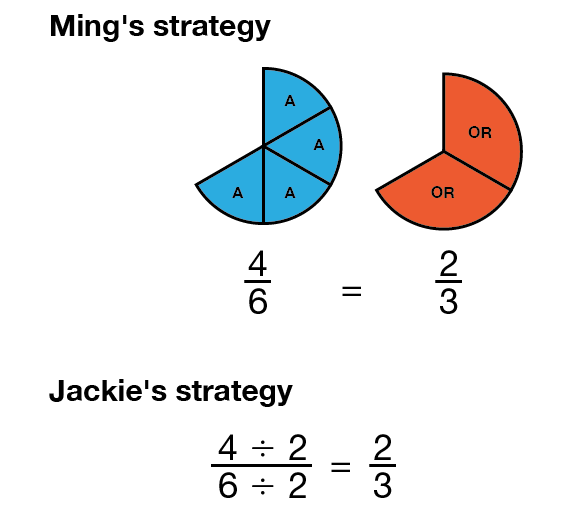
Methods for Finding Equivalent Fractions. Read Grace's and Josh's methods for finding equivalent ratios with the class. In Questions 15–16, students should recognize that Josh's method is incorrect. Ask questions like those in the sample dialog.

Students practice finding equivalent ratios in Questions 17 and 18. Encourage students to find equivalent ratios by using fraction pieces, multiplying the numerator and denominator by the same number, and dividing the numerator and denominator by the same number.

Use Check-In: Questions 18–20 in the Student Guide to assess students' abilities to use circle pieces, tables, or graphs to find equivalent fractions and ratios [E1].

The Workshop in Lesson 6 provides targeted practice with this expectation.

Teacher: Do you agree with Josh's way to find an equivalent ratio?

Ming: I don't. There's no way 1/4 is the same as 6/9.

Teacher: Why not?

Ming: Because 6/9 is more than a half and 1/4 is less than a half. They're not even close!

Teacher: So you compared both ratios to 1/4 and found the two fractions cannot be the same. Does anyone disagree with Ming?

Nicholas: Well, the answer seems wrong, but it looks like Josh did it right. He did the same thing on top as on the bottom, just like Grace's way.

Teacher: Was it just like Grace's way?

Keenya: Not really. He added the number to the top and bottom. Grace multiplied. You can't do it Josh's way.

Teacher: Why not?

Keenya: It doesn't work. But I don't know why.

Teacher: Try it out on another ratio, like 1/2.

Keenya: So if you added 2 to the top and bottom, you'd get... 3/2. That's more than one. It's not the same as 1/2 anymore.

Jackie: I think it only works if you multiply by the same number, not add. If you take 1/2, then multiply the 1 by 2 and multiply the 2 by 2, that gives you 2/4. That's still like 1/2.

Teacher: Good, Jackie. So we can multiply the top and bottom of a ratio by the same number to get an equivalent ratio. What about 4/6? What is an equivalent ratio for 4/6?

John: If you multiply top and bottom by two, you get 8/12.

Teacher: So if you multiply the numerator and denominator both by two, you get 8/12. Did anyone find a different equivalent ratio for 4/6?

Ming: What about 2/3?

Teacher: How did you find that?

Ming: With fraction pieces. Four aquas is the same as two oranges. [See Figure 4.]

Jackie: Or you could divide the top and bottom by two. That gives 2/3 too. [See Figure 4.]

Teacher: So it looks like we can also find equivalent ratios by dividing the top and bottom of a fraction by the same number.