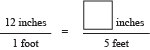Begin this Lesson by asking:
- What are some of the different ways that you can measure length? (Possible responses: inches, feet, yards, centimeters, meters, decimeters)
- If your friend tells you he is 4 feet 8 inches tall and you know that you are 54 inches tall, how can you figure out which one of you is taller without measuring? (Possible response: I would need to either think about how many inches are equal to 4 feet and then add the 8 inches, or I would have to find how many whole feet and extra inches are in 54 inches.)
- How can you figure out how many inches are in 4 feet? (Possible response: Since I know there are 12 inches in each foot, I can multiply 4 × 12 = 48 to see that there are 48 inches in 4 feet.)
- How can you find out how many feet are in 54 inches? (Possible response: Since I know there are 12 inches in a foot, I could divide 54 ÷ 12 = 4 with 6 left over to see that 54 inches is equal to 4 feet 6 inches.
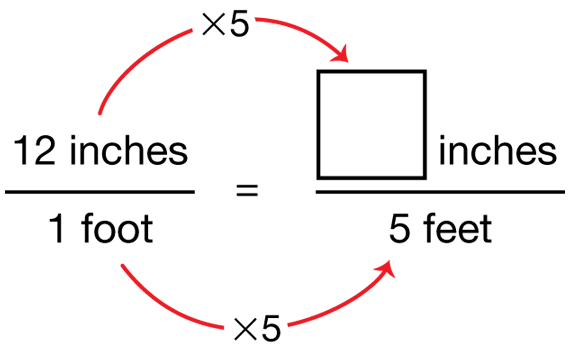
Explain that when you know the relationship between measurements you can use equivalent ratios to convert between them. Write the following number sentence on a display:
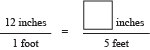
- What do you notice about the relationship between the denominator in the first ratio and the denominator in the second ratio? (Possible response: The denominator in the second ratio is 5 times the denominator in the first ratio.)
- How can you use this relationship to help you find the missing numerator in the second ratio? (Possible response: To find the missing numerator, I multiply the numerator in the first ratio by the same number you multiplied the denominator by. So for this ratio, I would multiply 12 × 5 = 60 to find the missing numerator.)
Add arrows to the number sentence to show how you can use the relationship between the denominators to find the missing numerator. See Figure 1.
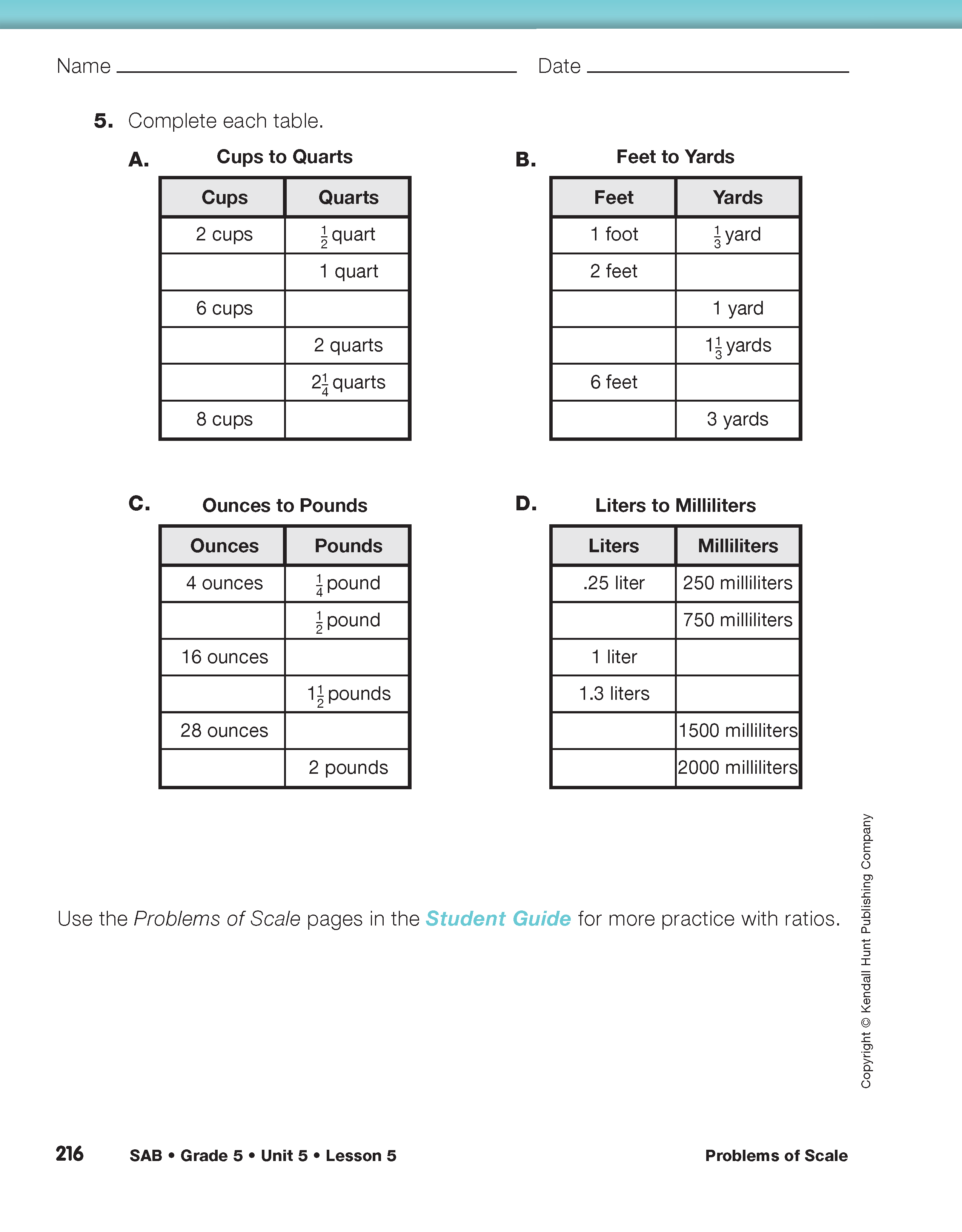
Direct students to the Using Ratios in Measurement pages in the Student Activity Book and have students work with a partner to complete Questions 1–5. After students have had time to work on these problems, ask several to share the strategies they used to solve each problem.
Use these or similar prompts to help guide the discussion:
- How did you find the length of the table in inches? (Possible response: Since the table is 6 feet long, I multiplied 6 × 12 = 72 to find that the table is 72 inches long.)
- The width of the door was 30 inches. How did you decide the width of the door in feet? (Possible response: If you divide 30 by 12, the answer is two with six left over. The two tells the number of feet and the six tells you there are 6 inches left. The width of the door is 2 feet 6 inches or 21/2 feet.)
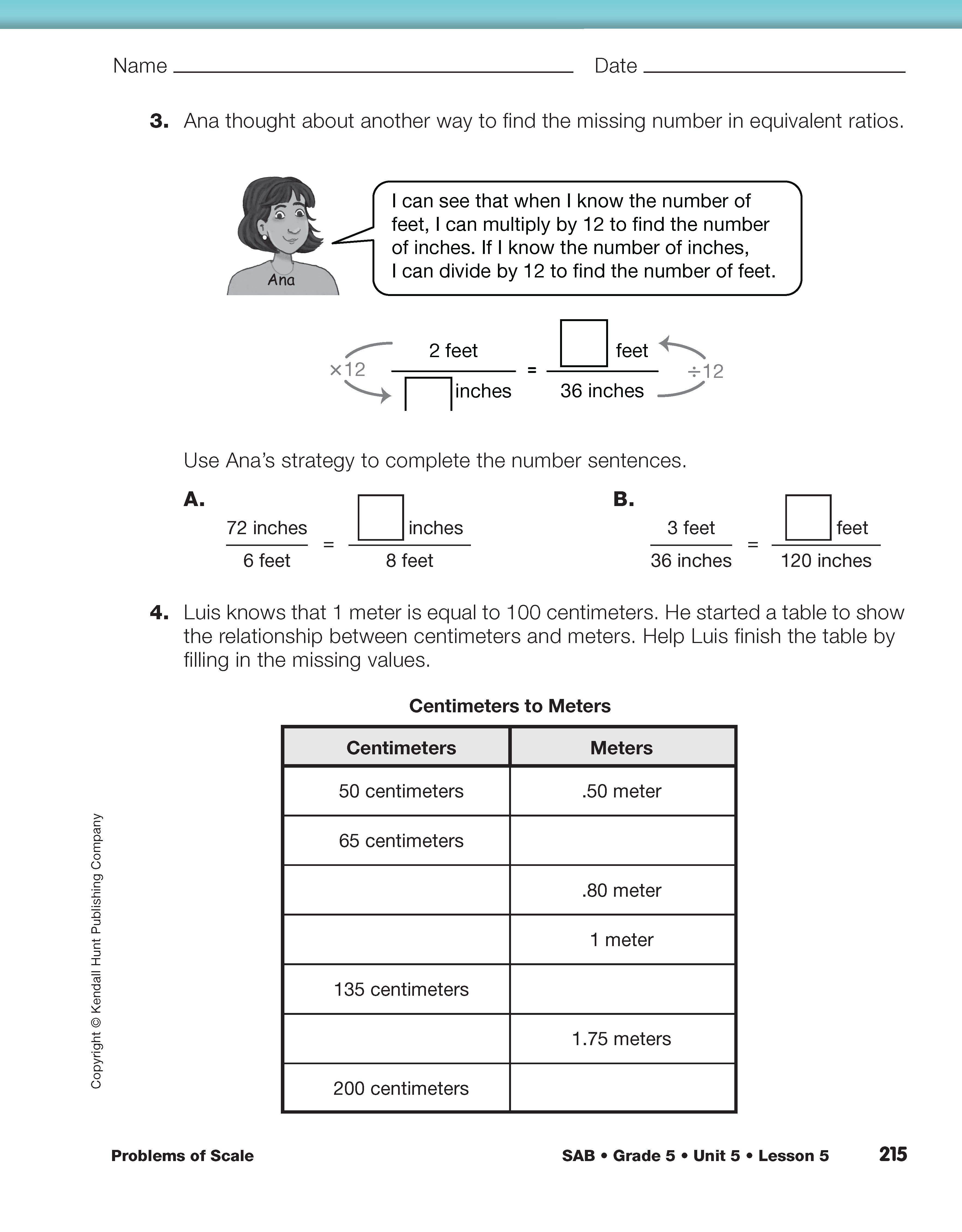
- How did you use Peter's strategy to solve Question 2A? (Possible response: When I look at the denominator in the first ratio, I can see that I need to multiply it times 4 to get the denominator in the second ratio. That means I have to multiply the numerator in the first ratio by 4 to get the numerator in the second ratio. 12 × 4 = 48, so there are 48 inches in 4 feet.)
- How is Ana's strategy different from Peter's strategy? (Possible response: In Peter's strategy you look at the relationship between the two ratios using either the numerators or the denominators. In Ana's strategy you look at the relationship between the numerator and denominator in one ratio and then use that relationship to find the missing value in the second ratio.)