How Close Is Close Enough

Est. Class Sessions: 1–2

Developing the Lesson

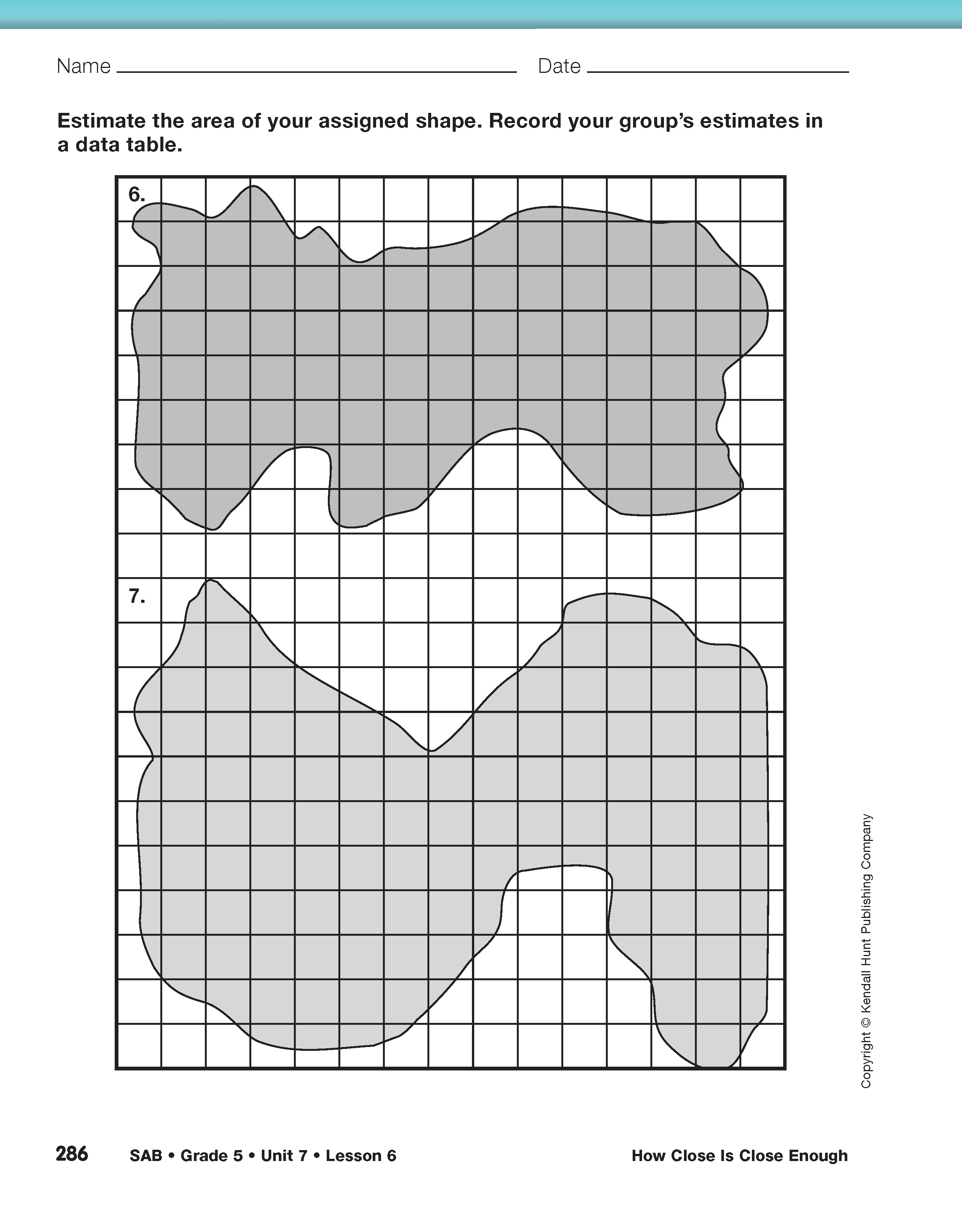
Part 1. Area of Irregular Shapes

Estimate Areas. To begin the activity, discuss students' strategies for finding the area of a shape with curved sides. Sketch an irregular shape on a display of Centimeter Grid Paper. Ask students to review strategies for estimating area. Make sure that the following different strategies are discussed and listed on the board or a display:

enclosing the irregular shape in a rectangle and finding the area of this rectangle for a very rough estimate;
counting full square centimeters and combining fractional units to make more whole units;
enclosing the shape in a rectangle, finding the area of the rectangle, and then subtracting the estimated number of square centimeters within the rectangle that are not part of the shape;
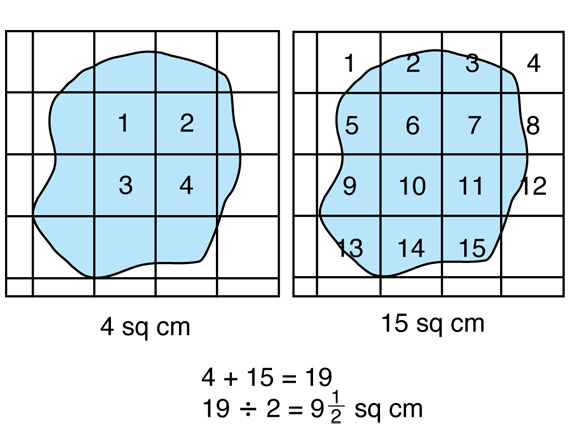
counting all squares completely filled by the shape, counting all squares completely enclosing the shape, and then averaging these two areas. See Figure 1 for an example.

After this discussion, put students in groups and ask each group to use one of these methods to estimate the area of two shapes on the Shapes pages in the Student Activity Book. Have each group choose one large shape and one smaller shape. Make sure that at least two groups are estimating the area for each shape.

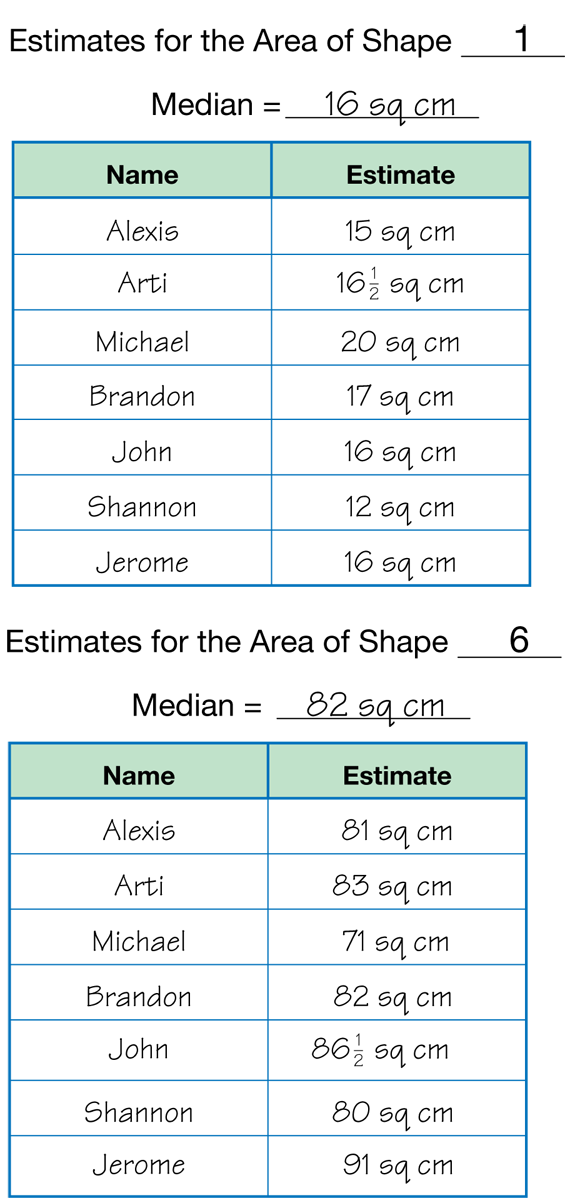
Each student in the group should independently make estimates of the areas of the two shapes. The group members share their measurements by recording them in a data table. Student groups can hand draw the data tables or use copies of the Two-Column Data Table Master. See Figure 2.

Once all the members have recorded estimates, the group finds the median estimated area for their shapes. Instruct them to record this information at the top of their data table.

When all groups have finished their data collection, choose one of the larger shapes, either Shape 6 or Shape 7. Ask the groups assigned to that shape to share their estimates. Make a table on the board or on a display of a Two-Column Data Table Master and combine all the estimates into one table. Have students determine the new median.

Use a Number Line to Compare Estimates. The following discussion prompts use the estimates in the data tables in Figure 2 as examples. Use the prompts to help guide a discussion on what it means to be “close” using your students' data on one of the shapes. Tell students that the exact area of each of the irregular shapes cannot ever be found. By finding the median estimate, we average out the errors in our measurements. We can usually assume the median is our best estimate of the actual measurement. In this case, using the sample data in Figure 2, the median for Shape 6 is 82 sq cm.

Ask:

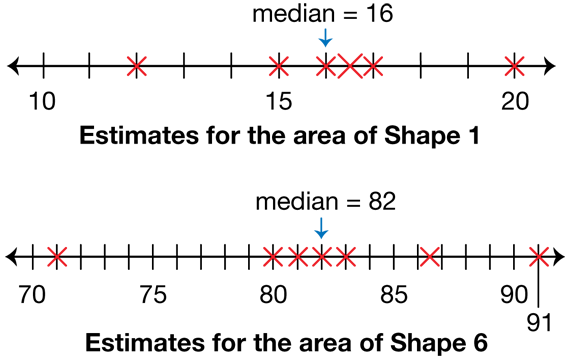
Whose estimates match the median exactly? (One or two of the students' estimates might match the median. It is less likely for larger areas like Shape 6 than for smaller shapes such as Shapes 1 and 2.)
Whose estimates are close to the median for Shape 1? (More students will be able to say that their estimates are close.)

Draw a number line or use your classroom number line. Mark or point out where the estimates, including the median, fall on the number line. Figure 3 shows number lines for the sample data for Shapes 1 and 6.

Ask:

Is there a “cluster” of estimates around the median? Describe how the estimates fall on the number line.

The students' estimates likely will cluster around the median. The number line for Shape 6 shows that the data clusters around 82 sq cm.

Ask:

Which estimates are close enough to the median to be good estimates? How much larger or smaller can your estimate be and still be a good estimate?

Let students choose a range of values that makes sense to them. Using sample data on the number line in Figure 3, students may say that close estimates are the ones closest to the median of 82 sq cm, or from 80 to 83 sq cm. Others may want to include the point at 87 sq cm. Students will likely not name estimates that lie as far away as 91 and 71 sq cm as good estimates. They may say that the estimates must be within 5 square centimeters to be close. For example, if the median estimate for the area is 82 sq cm, then students may choose to accept estimates in the range of 77 to 87 sq cm. Any reasonable range will do for now.

Now do the same with the estimates for a small shape such as Shape 1. List all the estimates made for this shape and have students find the median. Put the estimates on a number line.

Ask:

Describe where these estimates fall on the number line. What do you notice about these estimates?
Whose estimates match the median exactly?
Whose estimates are close?
Which estimates are close enough to the median to be good estimates? How much larger or smaller can your estimate be and still be a good estimate?

Accuracy and Precision in Measurement. The accuracy required in a measurement depends on the use we are going to make of the measurement. Any measurement we make in the real world is an estimation. If we measure the length and width of a rectangle to be 5.1 cm and 4.2 cm and multiply to find the area, we might report it as 21.42 sq cm. However, if the rectangle is really closer to 5.16 cm than 5.1 cm, we could not tell this with our ruler, which is only divided into tenths of a centimeter. So, in this example, the measurements we make are really estimates that are accurate to the nearest tenth of a centimeter. For our purposes, a measurement of 21.4 sq cm is probably more than sufficient.

If the measurement we make for a shape with straight sides, such as a rectangle, is an estimation, how then can we find the actual area of an irregular shape? We cannot. We can estimate by counting whole square centimeters and by piecing fractional units together to form more whole square centimeters. We can take several trials and cancel out possible errors in our work by finding the average or median value of the set of data. Then we can assume the median estimate is our best estimate.

Outliers in Data. When scientists see a measurement that is very different from the rest of the data, they may suspect that something went wrong with that measurement. In these cases, they sometimes, “throw out” that measurement when they analyze their data. Often they replace the measurement by taking another trial. The low estimate of 71 sq cm for Shape 6, for example, could be thrown out since it seems unreasonable in comparison to the other pieces of data.

Compare Median Estimates for Large and Small Irregular Shapes. At first, students may choose the same range of values as they did for the larger shape. For example, if the median estimate for Shape 1 is 16 sq cm, students may say that good estimates may also be within 5 sq cm of the median estimate. However, other students may feel that estimates as low as 11 sq cm and as high as 21 sq cm are not good estimates for Shape 1.

Ask students to think back to the reasonable range for the estimates of the area of the large shape.

Should you use the same range for this shape as you did for the large shape? For example, should you say any estimate within 5 sq cm is a “close enough” estimate? Why or why not? (Possible response using the sample estimates on the number line in Figure 3: All but two of the estimates are between 15 and 17 sq cm and all of them are no more than 4 sq cm away. So, 5 sq cm away is probably too far.)
Do you think it would be reasonable for a student to estimate the area of Shape 1 at 11 square centimeters? Why or why not? (No, it would not be reasonable. There are 9 full sq cm; at least 4 more almost full sq cm, and still quite a few more halves or partials. The area has to be at least 13 sq cm, so 11 sq cm is not a good estimate.)
Do you think that it makes sense to judge our estimates for both the large and small shapes using the same standard?

Students should begin to see that the larger the shape, the larger the range of acceptable estimates, and the smaller the shape, the smaller the range of acceptable values. It is clear that we cannot use a difference of 5 sq cm as our standard for both Shapes 1 and 6. Estimates within 5 sq cm of 82 sq cm for Shape 6, such as 77– 87 sq cm, can be considered good estimates. However, using the same standard for acceptable estimates for the number of sq cm in Shape 1 is not appropriate.

Ask:

If there are 474 students in the school, is an estimate of 500 students close enough? (In many situations, yes. The difference between the actual number of students and the estimate is 26 students.)
If there are 27 students in the classroom, is an estimate of 1 student close enough? (Obviously, no. The difference between the actual number of students in the class and this “estimate” is also 26 students.)
What happens to the range of acceptable estimates as the shapes get larger? (The range gets larger.)
What happens to the range when the shapes get smaller? (The range gets smaller.)