Modeling Division

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. The Column Method

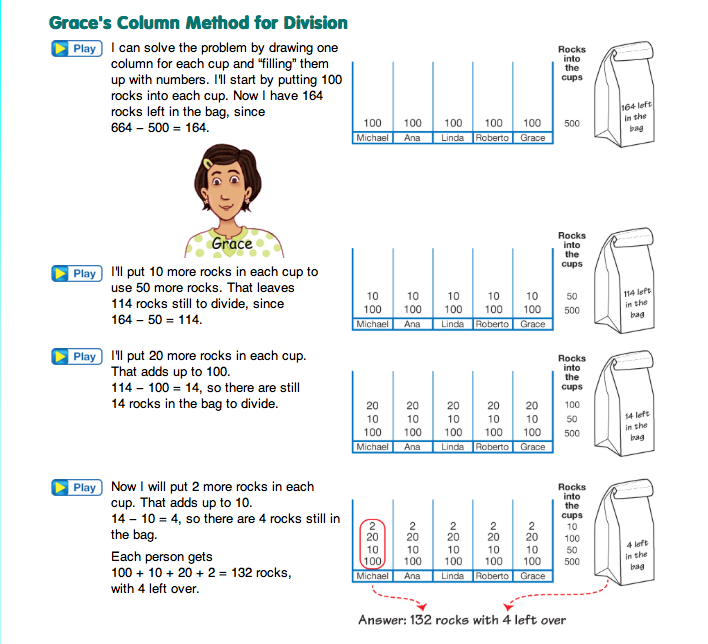
Model Division. Read the opening problem of the Modeling Division pages in the Student Guide as a class. Have partners discuss the problem about Grace's rocks using Questions 1–4. At this point, it is important that they not use a paper-and-pencil algorithm, such as long division or the partial quotients method, or a calculator to solve the problem. Encourage students to use words, drawings, and numbers to show their solutions. Be sure to allow enough time for students to work on their own methods before reading through Grace's method on the following page or suggesting computational strategies. This will provide a sense of how students approach division problems as well as their understanding of the underlying concepts.

After students solve the problem and check to see if their answers are reasonable as described in Question 4, ask two or three students to share their solutions with the class.

Introduce Grace's Column Method. Ask students to read through Grace's solution and then explain it to a partner. In her solution, Grace demonstrates the column method for dividing by a one-digit divisor. Explore the column method with the class using Questions 5–9 as a guide for the discussion. Be sure to discuss the meaning of the remainder and the conventions for showing the remainder in a solution to a problem. See Content Note.

Remainders. The convention of writing a remainder of 4 as “R4” or “r4” is one way among several of treating remainders. Remainders may also be designated using common language, such as “with 2 rocks left over.” Identifying remainders this way may help students connect remainders with the context of the problem. Depending on the context, remainders can also “push” an answer to the next highest whole number, can be discarded from an answer, or can be included with the quotient as a fraction. Each of these possibilities will be addressed more explicitly in later work on division.

Question 10 asks students to draw their own column model to solve 837 ÷ 5.

If students are ready to show remainders as fractions, they should be allowed to do so in situations when it is appropriate. In Grace's problem, for example, it would not make sense to cut the remaining stones into pieces. If the problem involved dividing candy bars, however, it would be appropriate to discuss how the remaining four candy bars might be divided among five friends. Students can use their familiarity with fractions to divide the remainder, 4, among 5 students, such that the quotient becomes 132 4/5.

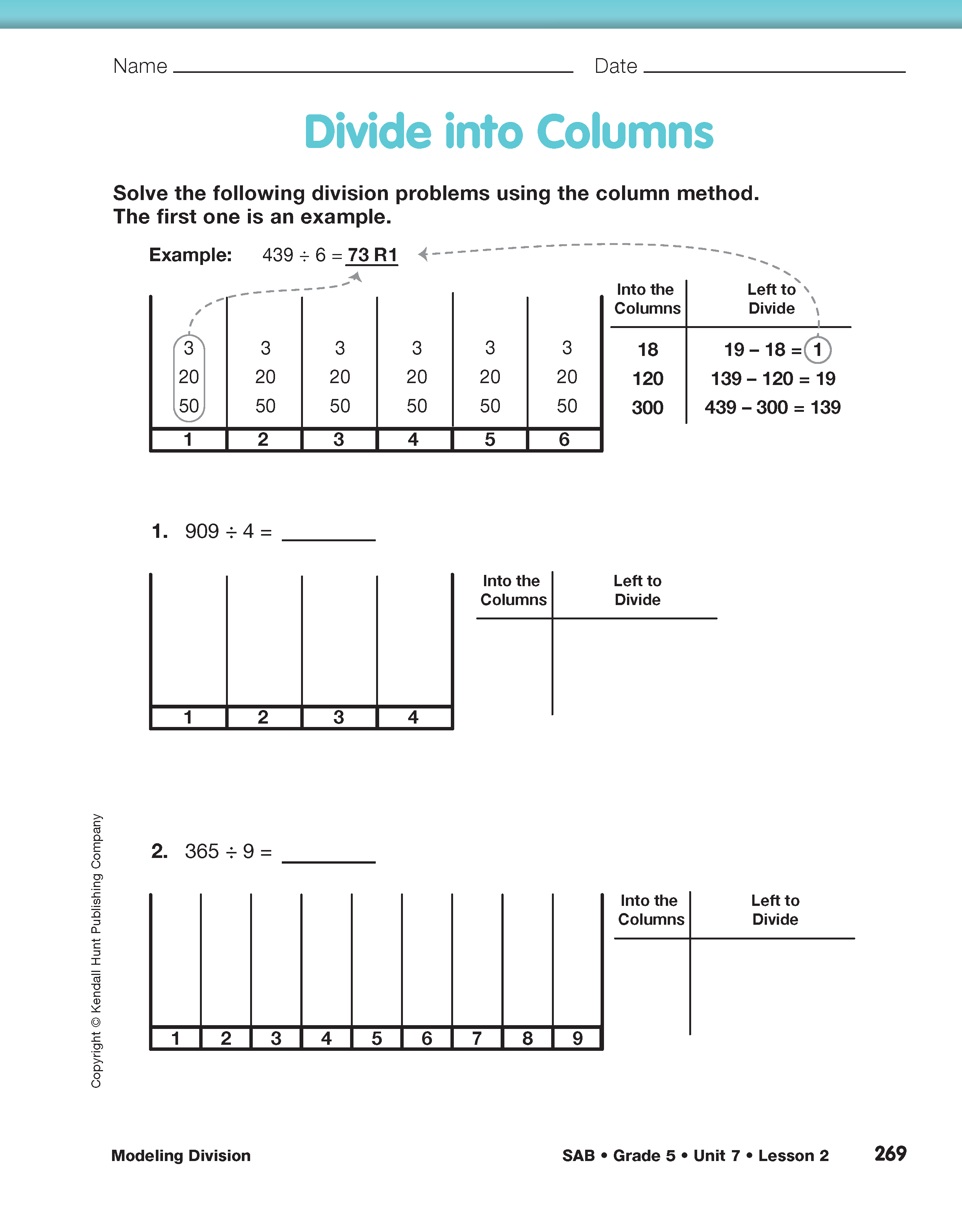
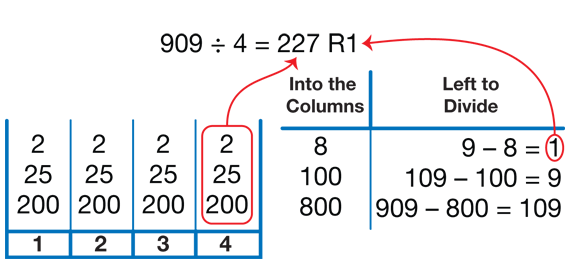
Practice the Column Method. Have students complete the Divide into Columns pages in the Student Activity Book. First, have students explain the example to a partner. As students work on the problems, ask questions to help students make connections between the representation and the division problems. See Figure 2.

Ask:

For Question 1, what is the division problem? (909 ÷ 4)
How is the divisor (4) represented in the column method? (the four columns)
What does 909 mean in this problem? (It is what you are dividing up, the dividend.)
When you divide it up, where do the parts go? (into the columns)
What numbers can you add and get the dividend, 909? (The 800 + 100 + 8 in the Into the Columns table plus the remainder 1. Also, if you add all the numbers in all the columns you get 908, then add the remainder 1 to get 909.)
Where does the 909 appear? (It is in the bottom subtraction problem in the Left to Divide column.)
What is the quotient (the answer)? Where does it come from? (227; Add the numbers in one column.)
Where is the remainder? (It is circled in the top subtraction problem in the Left to Divide column.)