Division and Data
This unit extends and applies students' knowledge of several topics: division, area, averages (means and medians), and accuracy in measurement and estimation.
DIVISION

Developing Flexible Models and Methods
In Unit 4, students developed a conceptual foundation for understanding multidigit… read more
Developing flexible models and methods
In Unit 4, students developed a conceptual foundation for understanding multidigit multiplication through the use of the rectangular array model, estimation, and mental math strategies. These models and strategies provide students with a range of methods to solve problems flexibly. They also allow students to make sense of paper-and-pencil methods for multiplication by linking efficient computation to an understanding of number, place value, and operations.
In this unit, a similar approach is used with division of multidigit numbers by a single-digit divisor. Students use various models and mental math strategies to develop foundational understandings about division. These include estimation strategies, a rectangle model similar to the model for multiplication, a tabular column method that illustrates equal distribution, the use of cluster problems, and the promotion of students' invented strategies that are mathematically sound.
Not only do these methods support sense-making about division, they also build on the connection between multiplication and division as inverse operations (NCTM, 2000; Van de Walle, 2006). Developing multiple strategies gives students the means to choose methods flexibly, so that they can solve different types of problems efficiently instead of depending on only one method.
The use of paper-and-pencil procedures grows out of the work students do with these less formal strategies. For example, the partial quotient method of long division emerges as a more efficient recording of the computations necessary for the rectangle model. The concrete and pictorial models link directly to the more abstract algorithms. The connections among them are clarified through use of the Division Strategies Menu (Figure 1). Additionally, a strong foundation in estimation enables students to use paper-and-pencil algorithms more accurately and efficiently (NRC, 2001). Therefore, it is important to give students ample time to develop the underlying concepts and skills necessary for understanding and doing division by working with the various models and strategies. This is true even if they have already learned a procedure for dividing using a paper-and-pencil algorithm.
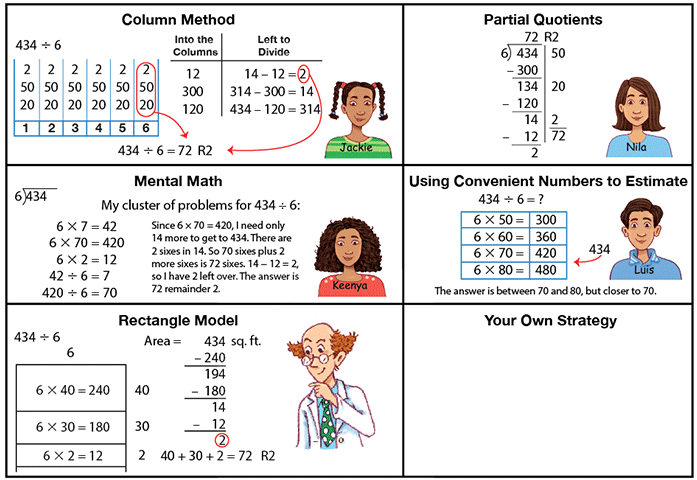
Figure 1: Division Strategies Menu
Types of Division
Students work with several types of division, all of which are important for students to… read more
Types of Division
Students work with several types of division, all of which are important for students to understand the basic operation. In one type, the number of groups is known but the number in each group is not, as with equal sharing. This type is known as partitive division. Alternately, the number in each group may be known and the number of groups is what needs to be found. This is typically known as measurement division. A third type of division, known as comparison division, occurs when two set sizes are being compared, (e.g., How many times as many apples are in Basket A as Basket B?) (Van de Walle, 2006). While these terms are not discussed specifically with students, each type of division is incorporated in the models that are used and in the way problems are posed.
Partial Quotients Method
In this unit, students learn a paper-and-pencil division method that is somewhat different… read more
Partial Quotients Method
In this unit, students learn a paper-and-pencil division method that is somewhat different from than the one traditionally used in the United States. This method, called the partial quotients method, does not require that the greatest quotient be found at each step, eliminating the frequent erasing encountered with the standard algorithm. Students who are taught the partial quotient method are better at solving unfamiliar problems and are better able to explain the meaning of the steps in the method than those taught the traditional method. This forgiving division method also gives students the opportunity to practice mental math and estimation strategies.
As an example of the partial quotients method, we divide 23 into 5256. (Note that even though the example here involves two-digit divisors, in this unit the division problems involve only one-digit divisors. In a later unit students will work with two-digit divisors.) There are 5256 marbles to be shared equally among 23 children. How many marbles will each child get? To begin, take a guess, say, 100. Write 100 on the right. Since 23 × 100 = 2300, write 2300 underneath and subtract to see how many marbles still need to be distributed.
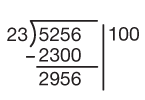
Figure 2: One possible first step in dividing 23 into 5256
Students should be encouraged to multiply 23 × 100 mentally, as discussed in Unit 3.
Next we estimate the number of 23s in 2956. It seems 100 is again a good choice.
Figure 3: A second possible step in dividing 23 into 5256
Students should look at the size of the remainder 656. They should see that 100 is now too big. That is, we cannot give 100 more marbles to each child. A student might choose 10 here and then 10 again as shown in Figure 4.

Figure 4: Two more steps in dividing 23 into 5256
At this point, 5 might be a good choice. See Figure 5.
With 81 remaining, a student might guess too high and choose 4. Only when the guess is too high do you have to erase. The last partial quotient is 3, leaving a remainder of 12. Adding up the number of 23s that divide 5256, we find 228. That is, 23 divides 5256 a total of 228 times with remainder 12. We distributed 228 marbles to each child with 12 left over. The 228 R12 can be written above the divisor as usual.

Figure 5: A final possible step in dividing 23 into 5256
Over time, students become better at mental estimation and the number of steps required with this method decreases. The partial quotients method closely resembles the traditional method if the best estimate is made at each step.
Content Note
The Partial Quotient. While this method may seem new, written record of it appears in a book published in 1729 while the first record of the traditional method appears in a publication dating from 1491 (Hazekamp, 1978). As with the traditional method, the partial quotients method requires students to estimate quotients. The partial quotients method is different in two ways. First, the student starts by estimating the entire quotient instead of the first digit. Second, if the estimate is too small, the student can continue with the procedure. This greatly alleviates the frustration of having to erase, and to some extent, allows one to get around a forgotten multiplication fact.
While practice with multiplication and division is provided in this unit and the Daily Practice and Problems, practice is distributed throughout the unit. Researchers find that spending more time in understanding procedures before practicing them aids recall and proficiency in the long run (Hiebert, 1990). Students should practice small numbers of problems for short periods of time spread out throughout the year.
While we have chosen methods to use to teach division, encourage students to share other correct methods of dividing—either those they learned previously, those learned from their parents, or those they invented themselves. Class discussions about other methods can greatly enhance understanding of division and also convey the message that problems in mathematics can be solved in many ways.
AREA

The area of a shape can be defined as the amount of space it covers. Beginning in… read more
The area of a shape can be defined as the amount of space it covers. Beginning in Third Grade, students find the area of shapes that do not neatly fall onto grid lines. As illustrated in Figure 6, students count whole square units and then put together the remaining pieces, trying to form full square units. The result is a good estimate of the area. Students use this technique in several activities in this unit, including the lab Spreading Out.
In this unit, we formally introduce the formula for finding the area of a rectangle. We also lay the conceptual groundwork for the introduction in a later unit of the formula for finding the area of a triangle.
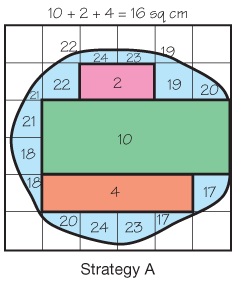
Figure 6: Strategy for finding the area of irregular shapes
MORE on AVERAGES

Averages are used throughout Math Trailblazers to find a representative value of a data… read more
Averages are used throughout Math Trailblazers to find a representative value of a data set. Beginning in First Grade, students find the median (the “middle” value) of data collected in laboratory experiments and other activities. In Fourth Grade, students begin using the mean to represent a data set. Earlier this year, students examined a third kind of average, the mode (the most common value). In this unit, students extend their understanding of averages by analyzing how different kinds of averages sometimes result in varied interpretations of data.
HOW CLOSE IS CLOSE?

Virtually all math educators agree that estimation should be an important part of the math… read more
Virtually all math educators agree that estimation should be an important part of the math curriculum. As students practice estimation, the question inevitably arises whether the estimate is close to the desired result. This is particularly apparent in the laboratory experiments in Math Trailblazers where students often make predictions based upon patterns in data and then check their predictions experimentally.
The most fundamental idea about “closeness” is that it is a relative idea. For example, suppose two merchants are selling the same item and the prices differ by $1. Whether the prices are close depends upon whether you are buying, for example, a new car for $20,000 or a cup of coffee for $2. As this example illustrates, when comparing the closeness of numbers or measurements, we need to think about the size of the numbers, not just the difference between them.
In this unit, we consider an estimate to be closer if it falls within a reasonable range of the median value.
MATH FACTS and MENTAL MATH

This unit continues the review and assessment of the multiplication and division facts… read more
This unit continues the review and assessment of the multiplication and division facts to develop mental math strategies, gain proficiency, and to learn to apply multiplication strategies to larger numbers. Students will focus on the multiplication and division facts for the last six facts.
Resources
- Hazekemp, D.W. “Teaching Multiplication and Division Algorithms.” In Developing Compuational Skills: 1978 Yearbook, M.N. Suydam and R.E. Reys, eds. National Council of Teachers of Mathematics, Reston, VA, 1978.
- Hiebert, J. “Relationships Between Research and the NCTM Standards.” Journal for Research in Mathematics Education, 30 (1), pp. 3–19. 1999.
- Hiebert, J. “The Role of Routine Procedures in the Development of Mathematical Competence.” In Teaching and Learning Mathematics in the 1990s, 1990 Yearbook, T.J. Cooney and C.R. Hirsch, eds. pp. 31–40. National Council of Teachers of Mathematics, Reston, VA, 1990.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
- van Engen, H., and G.E. Gibb. General Mental Functions Associated with Division, Iowa State Teachers College, Cedar Falls, IA, 1956.
- Van de Walle, J.A., and L. Lovin. Teaching Student-Centered Mathematics: Grades 3–5. Pearson Education, Boston, 2006.











