Spreading Out

Est. Class Sessions: 4–5

Developing the Lesson

Part 4. Communicate Problem Solving Strategies

Use Ratios and Graphs. In this part of the lesson, students will solve an extended response problem and explain their problem solving strategies. Students will use their data table, graph, and their understanding of ratios to help them. Before students begin the problem, ask them to look at their solutions for Questions 14–15.

Ask:

In Question 14 you were asked to write a ratio using points on the best-fit line. What strategy did you use to do this? (Possible response: I found 2 drops on the horizontal axis and then I followed the line up to my best-fit line before reading across to the vertical axis. I saw that the area was equal to14 square centimeters for 2 drops of water. The ratio would be 14 square centimeters/2 drops.)
In Question 15, two brands of paper towels were compared. How can you use ratios to decide which brand of paper towel was the most absorbent? (Possible response: You can look at the number of drops it takes to make a spot with the same area for each paper towel. The paper towel that has the spot with the smallest area is the most absorbent because it can hold more drops in all. For example, the area of the spot for four drops of water for the Super Soak towel is about 13 square centimeters so the ratio will be 13 square centimeters/4 drops. When you look at the Absorb-Plus towel it will only take about 21/2 drops to make a spot with an area of 13 square centimeters, so that ratio will be .)

Understanding the Problem. Provide each student with a copy of the How Many Drops Assessment Masters. Ask students to read the problem carefully and to think about what it is asking them to do.

Ask:

What is this problem asking you to do? (Find the number of drops of water that a whole piece of paper towel will absorb.)
What are some of the ways you have already represented the absorbency of your paper towel? (We collected data and organized it in a data table, we graphed our data and drew a best-fit line so we could make predictions, and we used ratios.)

Tell students that they will use all of this information to help them solve the problem on the How Many Drops Assessment Master.

Ask students to first work independently on the problem. After a few minutes, students can work with their partner(s). As students are workings, circulate around the room listening to solution strategies. Support students who need help clarifying their thinking and managing the multiple steps of this problem. See Sample Dialog.

Use this Sample Dialog as a model of a discussion about the multiple steps in this problem.

Teacher: What do you think you need to know about your paper towel to help you decide how many total drops it will hold?

Paul: I need to know the size of the towel.

Teacher: What measurement should you use to define the size?

Paul: The area.

Teacher: What is the side length of the towel?

Paul: 28 centimeters.

Teacher: What is the area?

Paul: 28 × 28 [uses calculator] 784 sq cm. [records on paper]

Teacher: That is the area of . . . ?

Paul: The whole sheet of paper towel.

Teacher: What do you need to do now?

Paul: Find the area of the spot.

Teacher: How did you figure that out?

Paul: [picks up a ruler and the spot and measures the side length of the square enclosing the spot] 61/2 or about 7 cm by 5 cm is 35 sq cm. [records on paper]

Teacher: Okay, so the area is 35 sq cm, and this area [referring to whole paper towel] you've written down.

Paul: 784. So we have to divide 784 by 35. [picks up calculator] 784 divided by 35 equals 22.4.

Teacher: Can you just round it to the nearest whole centimeter?

Paul: 22.

Teacher: What are you going to do now?

Paul: [sits back in chair]

Teacher: So, you know that this area [holding up whole paper towel] is 20 times greater than this area [holding up spot]. How does this help you figure out how many drops?

Paul: We know there's 12 drops in here [referring to spot], so we multiply this by 12.

Teacher: What is this? 12 by what?

Paul: 12 by 22 [picks up calculator] equals 264.

Teacher: What is 264?

Paul: The number of drops in a whole paper towel.

Teacher: Okay. Is that an exact . . .

Paul: No, that's about, an estimate.

Teacher: All right. Now report in your own words how you figured it out.

Communicate Solutions and Problem Solving Strategies. Encourage students to talk about their solutions and the steps they used to solve this problem with their partners to help them organize their ideas before putting them in writing. The Meeting Individual Needs box provides some suggestions for way to share student thinking.

One way to meet individual needs is to vary the work-product. Some students are prepared to record their solutions in writing. For others, the writing is an obstacle, but their solutions should still be shared in some way. Below are some strategies for varying the work-product or supporting students before they record their solutions in writing.

Ask students to tell another group how they solved the problem first, then have them record what they did in writing or using other media like a video recorder.
Ask students to record explanations on a video recording device. Students can then play these back as they record their work in writing. The video-recorded explanations can also be made available for others to review and evaluate.
Have students display their group solutions on large pieces of chart paper for others to see. Students talk together during the creation of the poster and then the work is easily accessible for others to review and evaluate.
Have each student group explain their solution to you or to a classroom helper before they start to write their explanation. Ask clarifying questions and encourage students to describe what the numbers mean in the context of the problem.

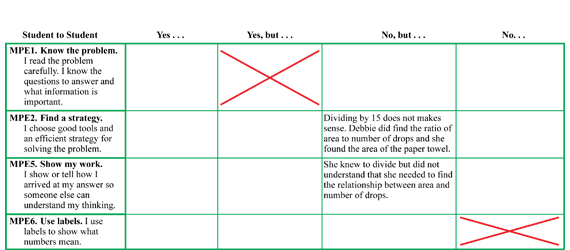
After students have had time to talk about their solutions, choose one or two pieces of student work to review to help set and clarify expectations for problem solving and communication. Ask students to look at either the display of the Math Practices page or the Math Practices page in the Student Guide Reference section. Tell students that they are going to focus of Math Practices Expectations 1, 2, 5 and 6 as they review the sample student work. Several of the strategies that can be used to solve this problem are shown in Figure 9.

Review George and Irma's Work. There are two samples of student work to serve as models for you and your class. Choose pieces of work from your own class to review and discuss as appropriate. After expectations have been discussed, give students time to revise the explanations they prepared earlier.

Use these or similar discussion prompts to review George and Irma's work in Figure 10. Display the How Many Drops Feedback Box Student-to-Student section on the How Many Drops Masters. Evaluate the work and give feedback to “George” and “Irma.” See Figure 11.

Ask:

What did George and Irma do to solve this problem? (They found the area of the whole paper towel and then used the ratio of 15/3 to find the number of drops in one sheet of paper towel.)
Where did the ratio come from? (In the lab questions we were asked to find a ratio using a point on the line, but George and Irma could have reminded us of that here and labeled the ratio—with “sq cm” and “number of drops.”)
How did George and Irma use the ratio? (Not sure. They have a number but they did not explain what they did to find 168.2.)
What would you do to find the number of drops using the ratio? (Using the ratio George and Irma gave us, 3 drops create a spot that is 15 sq cm. The area is 5 times greater than the number of drops, or the number of drops is 1/5 the area of the spot. So, I would divide the area of the sheet by 5 to calculate the number of drops.)
Do you think George and Irma divided the area of the whole sheet by 5 to find the number of drops? (Yes, I tried it and the calculations match.)
Did George and Irma label their numbers? (They did in their explanation but not in the ratios.)
Does their answer make sense? (yes) How do you know? (The relationship between the area and the number of drops is the same as the ratio taken from their graph.)

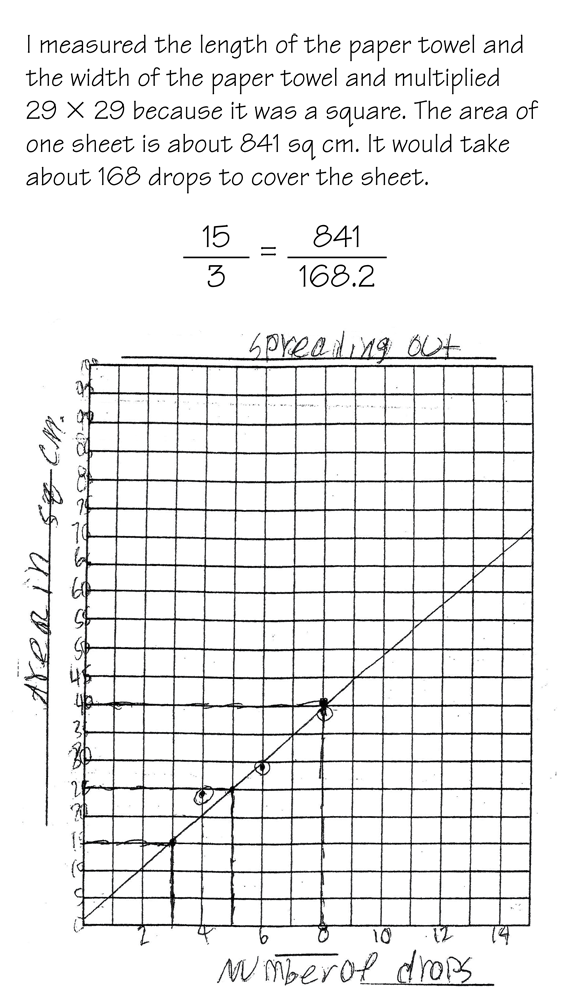
Review Debbie's Work. Ask students to look at Debbie's work. See Figure 12.

Use these or similar discussion prompts to review her work. Figure 13 shows a possible feedback box for Debbie.

What did Debbie do to solve this problem? (She found the area of the whole paper towel and then used the ratio of 15/3 to find the number of drops in one sheet of paper towel.)
Where did the ratio come from? (There is a point on Debbie's line for 15 sq cm/3 drops, but Debbie didn't show how she got it.)
How did Debbie use the ratio? (She divided the area of the sheet by 15. Debbie did not use the relationship between the area and the number of drops.)
What should Debbie have done with the ratio? (She should have divided the area of the whole paper towel by 5 since the area of the spot is 5 times larger than the number of drops.)
Did Debbie divide accurately? (no)
Did Debbie check her calculations or her answer for reasonableness? (no)
What should Debbie have done? (Possible responses: Debbie could look to see that the area is five time larger than the number of drops, so she could divide the entire area by 5. Debbie could use a calculator to check her division, or she could use multiplication to check her division.)
What would you tell Debbie to do to fix her answer? (Possible responses: Debbie could solve the problem using another strategy, like her graph or data table. To help Debbie see the relationship between the number of drops and the area of the spot, you could ask her the area of a spot with 2 drops, 5 drops, etc.)