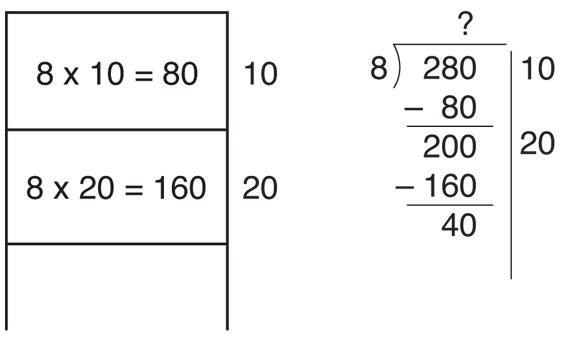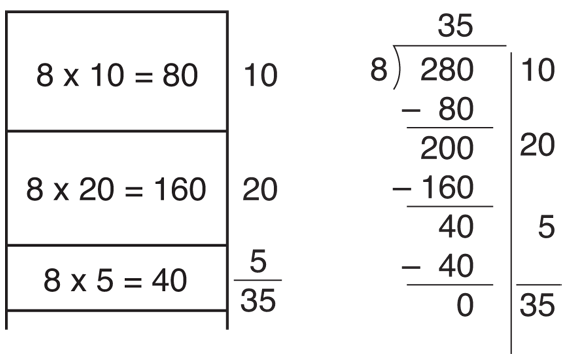Paper-and-Pencil Division
Est. Class Sessions: 2–3Developing the Lesson
Model Partial Quotients with Area Problems. In this lesson, students review a paper-and-pencil method, the partial quotients method, for solving division problems. We teach this method because many students find it easier to learn than the traditional method taught in the U.S. Both methods involve making estimates about the quotient, but the partial quotient method is more flexible. It allows students to underestimate and to work with easier numbers.
For a more detailed discussion of the partial quotients method, see the Mathematics in this Unit and the Letter Home.
As a warm-up activity, ask students to solve this problem:
Draw a picture of the hallway as in Figure 1 and encourage them to solve the problem by making and refining estimates as they did before. They can record their calculations any way they want. Explain that after they solve the problem, you will talk about an organized way to record their calculations.
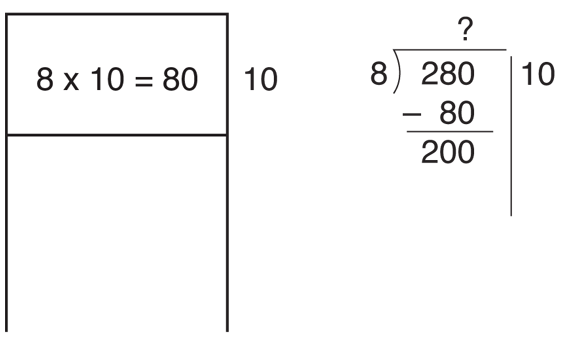
After students have solved the problem, ask a volunteer to share his or her solution. As the student describes the estimates in his or her solution, show how to record them in the partial quotients method. Figures 2–4 show each step as a student might write it using the rectangle model and the comparable step as written in the format of the partial quotients method.
In Figure 2, the first estimate is 10 feet. Multiply 8 × 10 = 80 shows that after painting 10 feet down the hall, 80 square feet of floor have been painted. Write 80 under 280 and subtract. There is enough paint remaining to cover another 200 square feet.
Figure 3 shows a second estimate of 20 feet. Multiply 8 × 20 = 160, write the product under the 200, and subtract. There is enough to cover 40 more square feet.
Figure 4 shows a third estimate of 5 feet. Multiply 8 × 5 = 40, write the product under 40, and subtract to get zero. Stop here. All the paint has been used. Adding the numbers on the right, the partial quotients, you see that 10 + 20 + 5 = 35 feet of hall were painted. We write the quotient 35 on top of the original problem so it can be easily seen.
280 ÷ 8 = 35
Compare Methods.
Ask students to compare the rectangle model with the partial quotients method:
Model Partial Quotient with Sharing Problems. Another way to think about division is with a sharing problem.
Pose the following problem and begin to solve it together:
Ask students if they recall a similar problem from Lesson 2. They should recall that in the opening problem, a collection of rocks was shared among 5 students.
Ask:
Ask students to estimate the answer:
Write student estimates on the board or a display to be checked after the problem has been solved completely.
Solve a Problem Using the Column and the Partial Quotients Methods. Ask students what amount they would choose for an initial distribution of the beads. Suggest using small, convenient numbers (numbers ending in zeros are good) at the beginning. Figures 5 and 6 show 20 as a first estimate, then 50, then 20 again, and finally 2.
As you work through the problem with the class, have a student write the estimates and calculations in the columns as you write them in the partial quotients format. Ask students to suggest possible estimates and ask them to explain what each number in the problem represents.
For example:
In this example we estimate that 7 goes into 504 fifty times. Then multiply 50 times 7 to get 350 and subtract. There are now 154 beads left to be distributed. We continue in this manner until no more beads can be distributed.
Continue to ask students what each number means.
Compare Methods. After finishing the problem, write the quotient (92) above the dividend.
Have students make comparisons between the two methods.
Ask:
Students can check the answer by multiplying to see whether the quotient times the divisor gives the dividend. That is, to check that 644 ÷ 7 = 92, check that 92 × 7 = 644.
Use Partial Quotients. Use the partial quotients division method together with several more problems:
448 ÷ 8 (Answer = 56)
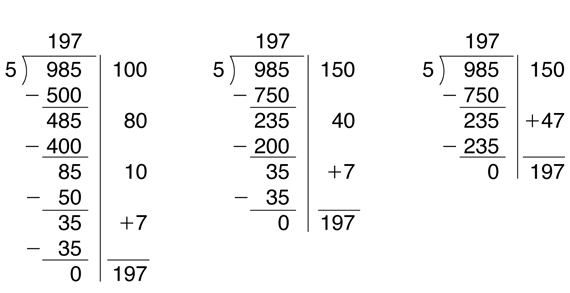
985 ÷ 5 (Answer = 197)
3456 ÷ 9 (Answer = 384)
For each problem, ask students to estimate their answers first. For example, 448 ÷ 8 is less than 60 since 8 × 60 = 480. It is more than 50 since 8 × 50 = 400. For the second problem, they can easily see the answer is more than 100 since 5 × 100 = 500 and it is less than 200, since 5 × 200 = 1000.
While the class is solving the problems, look for students who solve a problem using different estimates and therefore a different set of steps to complete the problem. Ask the selected students to record their solutions on the board side by side. See Figure 7.
Discuss similarities and differences in the steps:
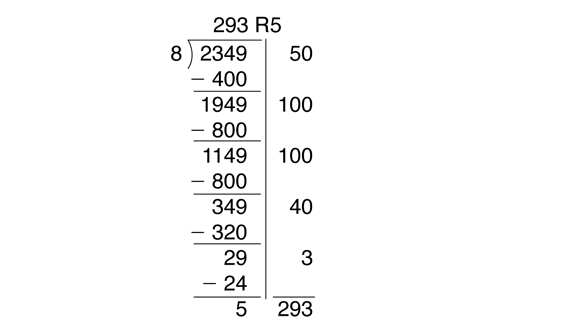
Solve Problems with Remainders.
Present an example with a remainder:
Begin by asking students to estimate the number of packages:
Ask students to solve the problems and share one or two solutions with the class. A sample solution is shown in Figure 8.
The discussion prompts that follow are adapted from a classroom discussion in which the teacher checked for students' understanding of the steps in the partial quotients method. These questions refer to the solution in Figure 8.
Ask:
Note that the problem in Figure 8 has a remainder.
Ask:
Students can quickly check this calculation on a calculator, or they can check with paper-and-pencil multiplication.
Practice the Partial Quotients Method. The Paper-and-Pencil Division pages in the Student Guide provide additional explanation and practice. Have students read and discuss the two examples in pairs. Each partner can explain one example to the other. The first example has a whole number quotient. The second has a remainder. Ask questions to check that students understand what the numbers mean in each step.
Have students complete Question 1 in groups. Ask them to explain the remainders. In Question 2, students check their answers using multiplication.
Question 3 presents four solutions to the same division problem. By now, students will have noticed that for each problem, there are several ways to choose partial quotients but they all result in the same answer. This makes the method very flexible and allows students to choose numbers they are comfortable working with. However, some choices are more efficient than others. When students are ready, they can start to look for choices that solve the problem in fewer steps.
Ask:
In general, when students choose partial quotients as large as possible (without going over), they will solve the problem in the fewest number of steps. In this case, the fourth solution has the same number of steps as the traditional long division method.
Have students complete Questions 4–5 in small groups or pairs. Have them compare their solutions and note the number of steps they used.
When students have completed Questions 1–5 in groups or pairs, have them work independently to answer Check-In: Questions 6–10. As they work, circulate and observe which students are ready to look for larger first estimates to solve the problem in fewer steps and which students are not. Encourage, but do not require, students to solve the problem using the fewest steps. Encourage students to choose numbers that are comfortable for them, even if it takes more steps.