Workshop: Division Strategies

Est. Class Sessions: 1–2

Developing the Lesson

Part 2: Division Strategies Workshop

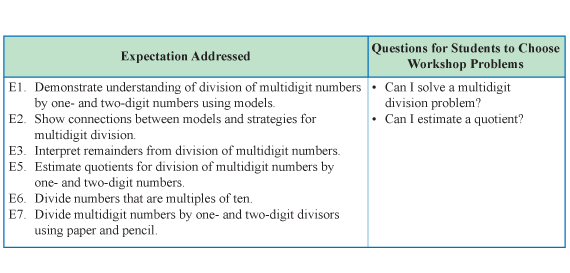
Choose Targeted Practice. The menu and problems for this Workshop are in the Workshop: Division Strategies pages in the Student Guide. Minis of these pages not shown here are in the Answer Key. This Workshop addresses Expectations as shown in Figure 6.

Students begin the Workshop with Self-Check: Question 1. This question serves two purposes. First, it clearly communicates the content of the related targeted practice to students. Second, it helps students quickly self-assess their progress with Expectations to help them choose which problems to work on in the Workshop.

Students use Self-Check: Question 1 and the menu on the Workshop: Division Strategies pages in the Student Guide to assess their abilities to use the rectangle model and the column method to divide [E1]; estimate quotients for division of multidigit numbers by one- and two-digit numbers [E5]; and divide multidigit numbers by one- and two-digit divisors using partials quotients [E7].

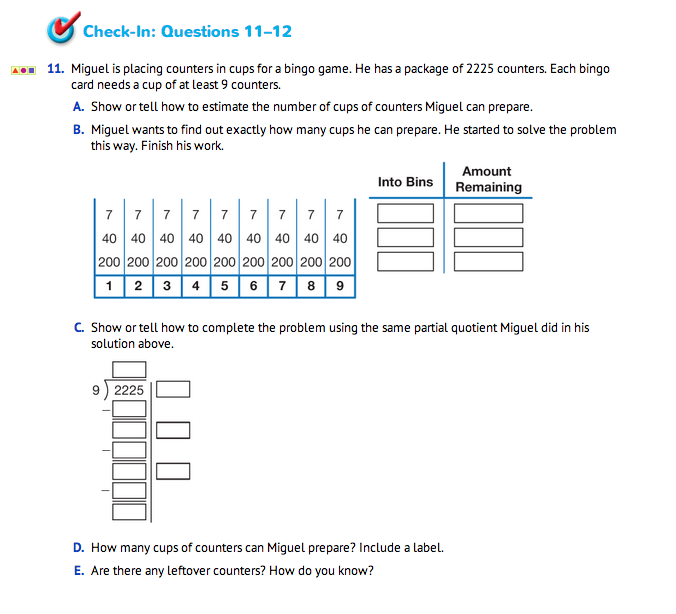
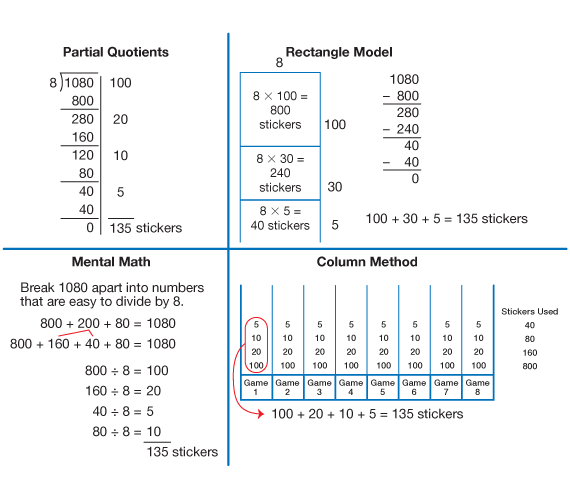
Direct students to the Workshop: Division Strategies pages in the Student Guide. Students should solve the problem presented in Self-Check: Question 1 individually. Encourage students to refer to the Division Strategies Menu in the Student Guide Reference section. They will solve the problem using partial quotients, a rectangle model, and the column method. Monitor students as they work and select students to show solutions using each of the division strategies.

Upon completion, ask these students to share their solution strategies with the class. See Figure 7 for sample solutions.

To facilitate discussion, ask questions such as:

What was your first estimate? How did you choose it? (Possible response: 150; I used numbers that were easy to multiply. I thought 8 × 100 = 800, but that was too low. 8 × 200 = 1600, and that is too high, so I estimated 150 stickers because it was in the middle.)
Show the [partial quotients, rectangle model, column method] strategy you used to find the exact answer. (See Figure 7.)
What do the numbers mean? (1080 is the number of stickers Jackie has, 8 is the number of games, and 135 is the number of stickers Jackie should place at each game.)
How did you label your answer? (stickers)
Which number shows the groups of stickers Jackie sorted? (Possible response: See Figure 7. For example, with partial quotients, first she puts 100 stickers in a group, then 20, then 10, then 5.)
Which numbers show the stickers not yet sorted in each step? (Possible response: See Figure 7. For example, with partial quotients, 280 shows how many stickers still need to be sorted after she groups them by 100s. Then 120 stickers are left to sort, and then 40 stickers.)
Are there stickers left over? (no)
How is that shown in this strategy? (Possible response: a remainder of 0)
Can you solve the problem using mental math or with a few quick notes? (See Figure 7 for an example.)
Explain an estimation strategy that will help us decide if the answer is reasonable. (Possible response: My answer is 135. 130 × 8 is 800 plus 240, which is 1040. That's very close to 1080, and if I add on 5 × 8 more, it is exactly 1080 so I know my answer is correct.)
Which strategy do you like best for solving this problem? Explain why.
Which strategy is the most difficult for you to use?

The problems on the Workshop: Division Strategies pages provide opportunity to practice using a variety of division strategies: mental math, the rectangle model, partial quotients, the column method, as well as estimation strategies. Refer students to the Workshop: Menu. Ask them to think about their work on Self-Check: Question 1, their progress with these Expectations, and the "Can I Do This?" statements and to choose from the following groups:

Students who are “working on it” and need some extra help should circle the problem set marked with a triangle (). These problems provide scaffolded support for developing the essential underlying concepts as well as some opportunities for practice.
Students who are “getting it” and just need more practice should circle the problem set marked with a circle (). These problems mainly provide opportunities to practice with some concept reinforcement and some opportunities for extension.
Students who have “got it” and are ready for a challenge or extension should circle problems marked with a square (). These problems provide some practice and then move into opportunities for extension.

Check students' choices to see how well they match your own assessment of their progress on the related Expectations. Help students make selections that will provide the kind of practice they need.

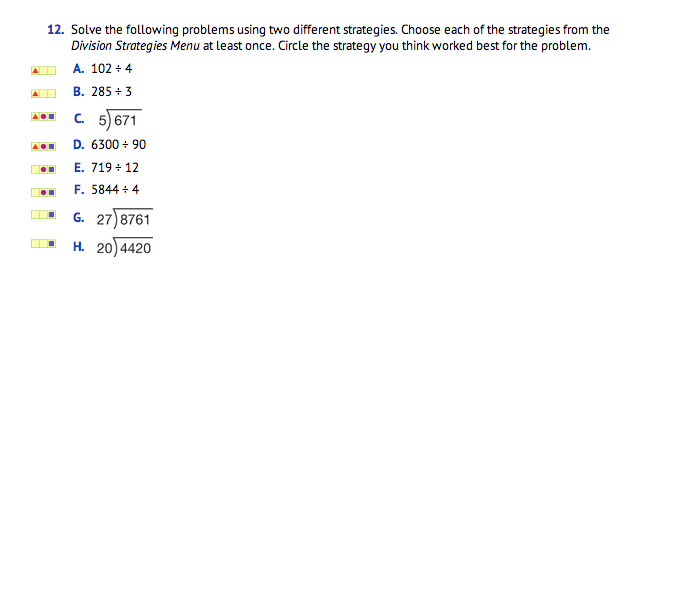
Solve Division Workshop Problems. Once students select the questions to complete in the Workshop, have them work independently or with a partner to solve the problems they chose. Match groups of students who have chosen similar sets of problems from the menu. Encourage students to use the Division Strategies Menus in the Student Guide Reference section as they are working.

As students are working, choose one or two students to clearly share their solutions to Check-In: Question 12C with the class during Summarizing the Lesson. Select students who will show a variety of solution strategies.

Students who complete their assigned set of problems can play Quotient Quest or Division Digits Game from Lesson 3.

Challenge students who are proficient with paper-and-pencil methods, but rely heavily on this procedure, to choose as many problems as they can to solve using mental math or a few quick notes.

Use Check-In: Questions 11–12 on the Workshop: Division Strategies pages in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to demonstrate understanding of division using models [E1]; show connections between models and strategies [E2]; interpret remainders [E3]; estimate quotients [E5]; divide numbers that are multiples of ten [E6]; divide multidigit numbers by one- and two-digit divisors using paper and pencil [E7]; know the problem [MPE1]; find a strategy [MPE2]; check for reasonableness [MPE3]; explain a solution [MPE5]; and use labels [MPE6].