Measure in meters, centimeters, and millimeters. Give each student pair a meterstick and one of the sheets of paper you prepared with a description of a distance in the classroom (e.g., length of desk). See Materials Preparation. Ask each student pair to measure that distance in centimeters, meters, and millimeters. Instruct students to record these measurements on the paper that describes the distance. Set a time limit for completing the task and then have students begin their measurement task. While students are working, circulate and listen to students negotiate, measure, and record the measurements.
- Your distance seems longer than the meterstick. How are you going to do that with only one meterstick? (Possible response: I will lay down the meterstick, make a mark, and then move the meterstick. I have to remember to start at zero each time.)
- Your distance seems shorter than a meter. How are you going to measure that distance in meters? (Possible response: I need to represent that part of the meter. The centimeter marks divide the meter into 100 pieces and the distance is 80 of those 100 pieces or 80/100 or 0.80 of a meter.)
- What unit are you using? Show me one of those units on the meterstick.
- How many millimeters are in one centimeter?
- How many centimeters are in one meter?
- I see you showed that distance with a common fraction. Write a decimal fraction for that same distance.
As students complete their measurements, ask them to display their papers on the board.
- What do you notice about each set of measurements? (Possible responses: The digits are the same but the decimal moves; the numerators and denominators are similar and they are multiples of ten of each other.)
- How are the measurements written? (Some used fractions and some used decimals.)
- I measured a distance to 55 cm. I want to measure this distance in meters. How many meters? (.55 m or 55/100 m)
- I want to measure this distance in millimeters. How many millimeters? (550 millimeters)
- What fraction of a meter is a centimeter? (1/100 of a
meter or .01 of a meter)
- What fraction of a meter is a millimeter? (1/1000 of a meter or 0.001 of a meter)
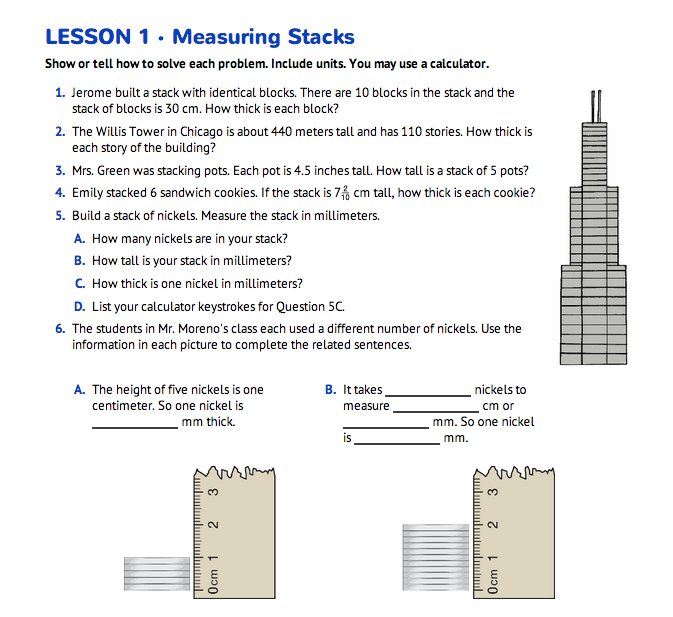
Solve Problems Involving Stacks. Read Question 1 in the Student Guide and ask students to solve the problem. Ask a student to share their solution for the problem as you illustrate the problem with a quick sketch on the board. Repeat this process with Question 2. Then ask students to solve and discuss Questions 3–4 with a partner. While students are working, ask each student pair to draw a picture to illustrate one of the problems and then show or tell how they solved the problem. Give each student pair one piece of paper to display this work. Be sure both problems are distributed among the students. Circulate among the students listening for students who are having trouble illustrating or solving the problem or who have interesting strategies for managing the decimals and fractions.
As students complete the selected problem, ask students to display their solution with the other solutions to the same problem. See Figures 1 and 2 for possible solutions. Discuss solution strategies to Questions 3–4.
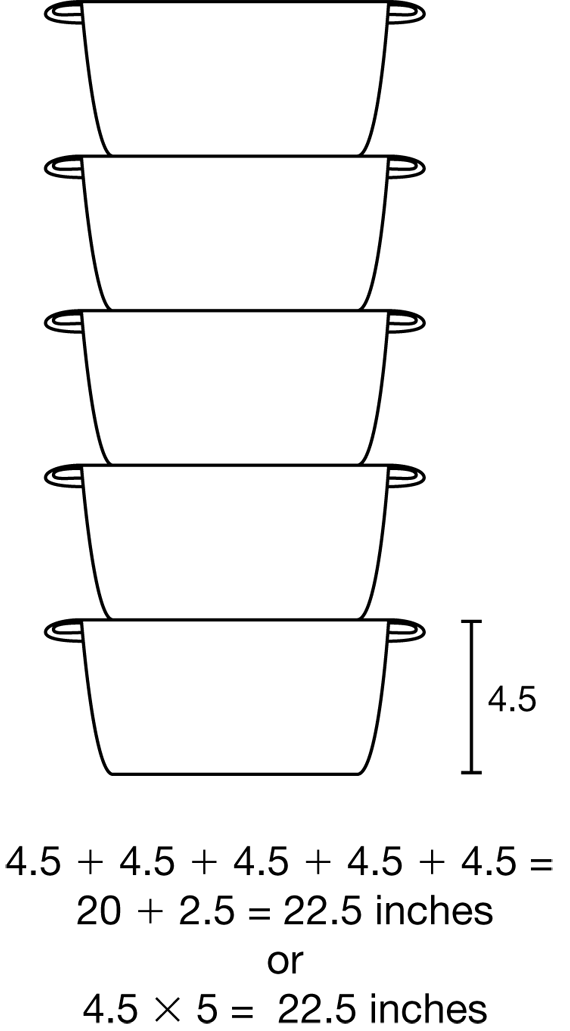
- In Question 3, what does 4.5 inches mean? What does the .5 mean? (5/10 of an inch or 1/2 of an inch)
- Find 4.5 inches on your ruler.
- What did you do to add the half inches in Question 3? (Possible response: I put the halves together to make wholes. Four halves make 2 wholes and there is one-half left over; I used a calculator to multiply 4.5 × 5.)
Stacking Coins. Give each student pair a collection of nickels. Ask them to measure the height of a stack of nickels and then calculate the thickness of one nickel as directed in Question 5.
- What did you do to calculate the thickness of one nickel? (I measured the stack and counted the nickels in the stack. I stacked 6 nickels and the stack measured 1.2 cm or 12 mm. I then divided 12 mm by 6 nickels and found that one nickel is 2 mm thick.)
Ask students to answer Questions 6–7 with a partner.
After students have completed these questions, ask:
- Did everyone find the thickness of a nickel to be the same? Why or why not? (Possible response: The thickness of a nickel is not consistent. If the nickel is new it is probably thicker. If it is old, it is probably worn down and not as thick. Dirt can also make the nickel thicker or not as thick.)
- What can you do to agree upon a thickness? (Use the thickness that comes up the most often [mode] or find the median thickness.)
Work with the students to agree upon the thickness of the nickel. Then assign Question 8.
- How did you figure out how many nickels are in $1000? (There are 20 nickels in $1 so there are 20,000 nickels in $1000.)
- How tall is a stack of $1000 in millimeters? (Possible response: 20,000 nickels × 2 mm = 40,000 mm)
- How tall is that? Taller than you? Taller than the school?
- Maybe you can estimate better if the answer is in centimeters. How many cm tall is $1000 of nickels? (Possible response: 20,000 nickels × .2 cm = 4000 cm)
- How tall is that? Taller than you? Taller than the school? (Possible response: a lot)
- Maybe you can estimate better if the answer is in meters. How many meters tall is $1000 of nickels? (Possible response: 20,000 nickels × .002 m or 2/1000 m = 40 m)
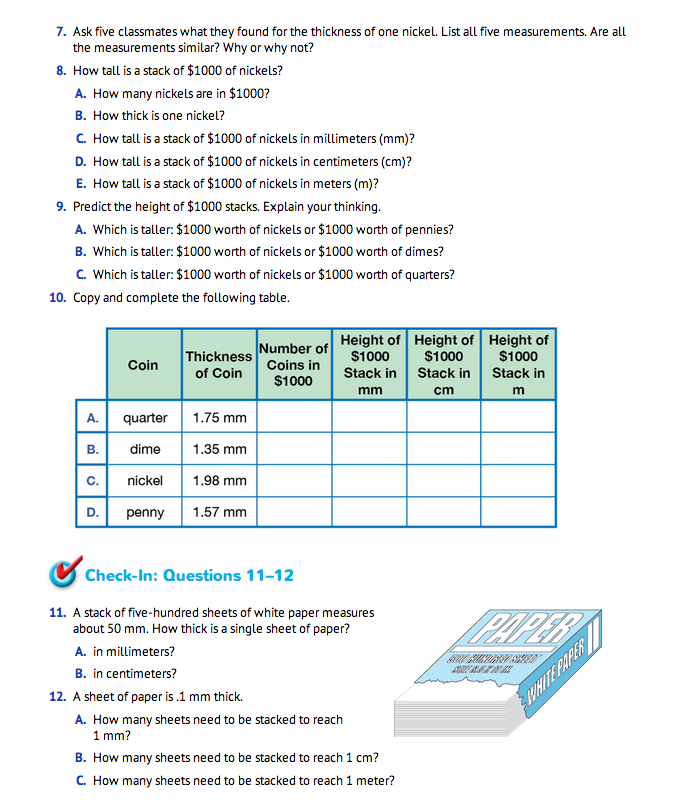
Ask students to work with a partner to solve Questions 9–12.
Use Check-In: Questions 11–12 in the Student Guide to assess students' abilities to recognize that in a multidigit number, a digit in one place represents 10 times as much as it represents to its right and 1/10 of what it represents in the place to its left [E5], and use the patterns in the number of zeros and the placement of the decimal point when a decimal is multiplied or divided by a power of ten [E6].