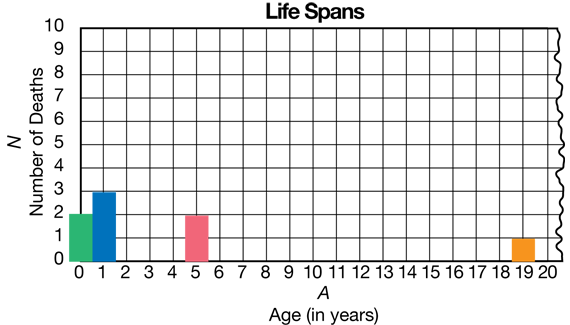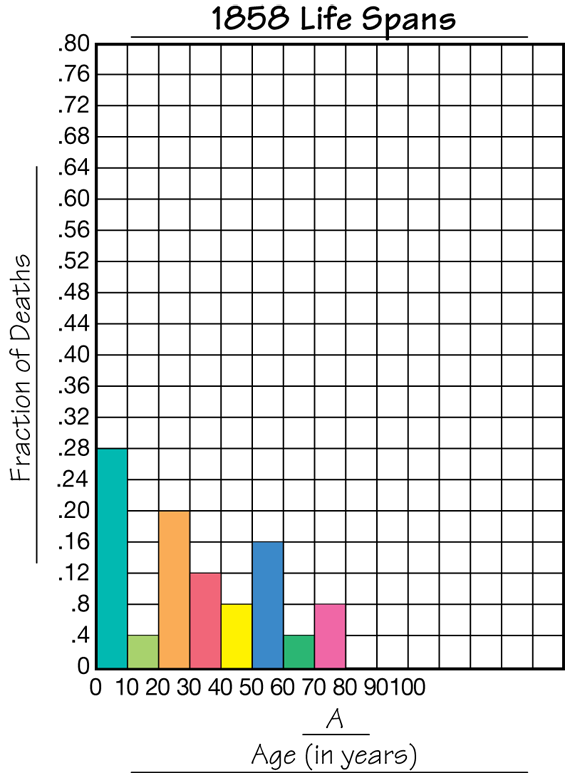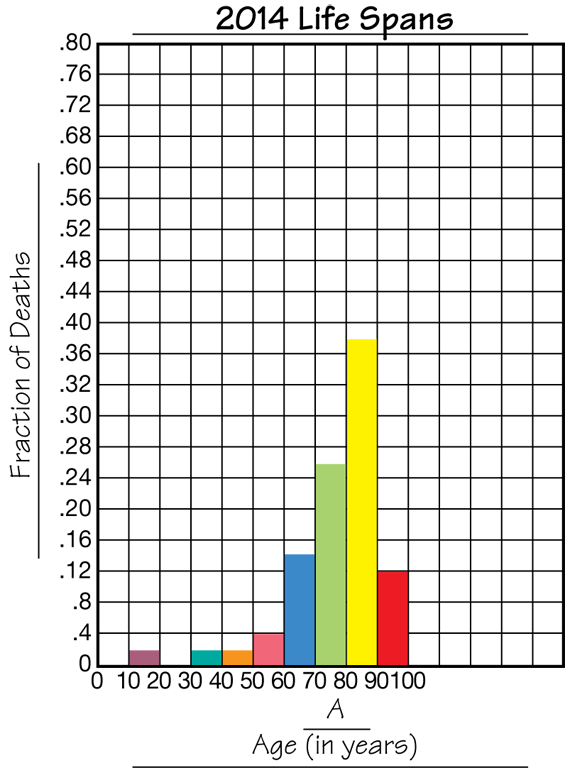Life Spans

Est. Class Sessions: 1–2

Developing the Lesson

Prepare to Organize the Data. Read the vignette on the Life Spans pages in the Student Guide. Discuss the information that David and Brandon gathered at the library, beginning with Question 1. Students can see that the ages at death listed in the 1858 data range from infancy to 79 years and the life spans in the 2014 data range from 15 to 97 years.

To discourage students from writing in their Student Guide, suggest that they write both of the data sets on their own paper. If they work in pairs, one partner can read the numbers while the other writes them down. Then, as you discuss the data, students can check off numbers as needed.

Students may find it difficult to find trends in the data as it is listed in the Student Guide. Question 2 suggests graphing the data as a way to tell the story of the data. It also asks how to set up the graphs. Students may have many suggestions.

Help students evaluate the different methods by asking:

What do we want to compare? (Life spans in the mid-1800s to life spans in 2014. Do people live longer in the twenty-first century?)
What data do we need to make this comparison? (We need to know how many people in each data set lived to each age. For example, how many people lived to be 60? How many lived to be 50?)
How can we find this data? (Make a new table and tally the number of deaths at each age.)
How would you graph this data? What variable would you put on the horizontal axis? What variable would you put on the vertical axis? (Put the age in years on the horizontal axis and the number of deaths at each age on the vertical axis.)
If you made a bar graph of the 1858 data, how would you need to scale the horizontal axis? (from 0 to 79)
If you scaled the horizontal axis by one, one for each age, will this graph fit on the graph paper? (No, this scale is not practical.)
How tall would most of the bars be? (Most of the bars would be very small. Since they would all be about the same height, they would not give much information.)

Figure 1 shows what the beginning of a bar graph would look like with the horizontal axis scaled by ones.

Suggest to students that they need a new way to organize the data to help them see trends in the data. In the Student Guide, Mr. Moreno suggests that students bin the data. Explain that you bin data so it will be easier to graph and so you can see patterns in the data better. As described in Question 3, ask students to look at the life span data and suggest possible intervals that can be used. One suggestion is to use intervals of 10 years. The intervals will then be 0–9 years, 10–19 years, 20–29 years, 30–39 years, and so on until there are bins for all of the data.

The intervals or bins should not overlap and should be the same size. For example, students should not choose intervals from 0–10 years, 10–20 years, or 20–30 years. Using these bins, students will not know where to tally life spans of 10, 20, or 30 years. Choosing the last bin to be “over 60 years” is also problematic, since this bin is larger than the others.

Question 4 asks students how they can compare data if their samples are different sizes. There are 25 life spans in the 1858 data and 50 life spans in the 2014 data. Students had some experience with this in Lesson 2. Remind students that when Lee Yah and her cousin compared data from their class survey on favorite sports, they found that they could more easily compare the data using decimals. Therefore, when you convert a fraction to a decimal, you are showing what part, out of 10 or 100, of your sample you are considering. This allows you to compare samples of different sizes accurately.

Binning Data. When there are many values and a wide range of values in a data set, it is often impractical to display the data using a bar graph without grouping the data into intervals or bins. For example, suppose a principal of a large school collects data on the number of miles teachers drive to school. He finds that the number of miles teachers drive ranges from 1 to 50 miles and no two teachers drive the same number of miles to school. It is not useful to make a bar graph with a scale of 1 to 50 miles on the horizontal axis and one bar for each different number of miles driven. The horizontal axis would be too long and all the bars would be the same height. It is better to group the data into equal intervals or, as we say, to “bin” the data. In this case, the data can be divided into intervals such as 0–9 miles, 10–19 miles, 20–29 miles, etc. Then a bar can be drawn for each interval. Note: The bars are drawn between the lines to show that the data lie within the interval. For example, the first bar tells us that ten teachers drive between 0 and 9 miles to work.

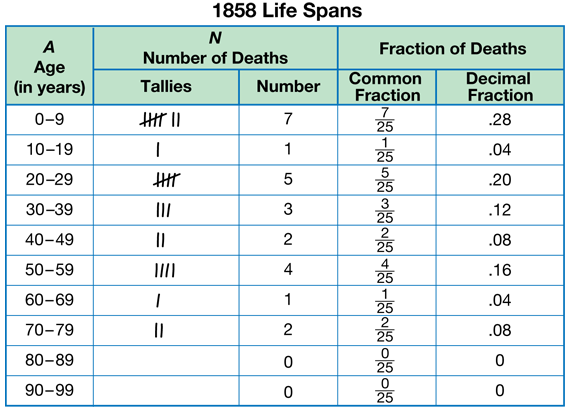
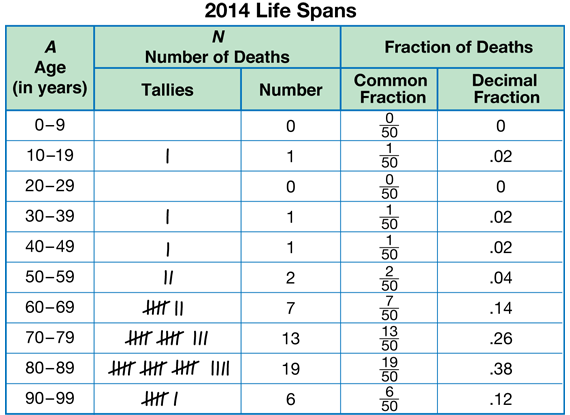
Organize the Life Span Data. In Question 5, students are directed to organize the data into bins using the Life Spans Data Tables page in the Student Activity Book. See Figure 2 for a sample completed data table for the 1858 data. Note that the intervals are the same size and that they do not overlap.

After students have had a chance to bin the data, ask:

What fraction of the people died when they were in their [20s]? (5/25)
What does the denominator represent? (It is the number of people in the survey.)
What does the numerator mean? (It is the number of people of that age that died.)
Did more people die in their 20s or 30s in 1858? (More people died in the 20s.)
How do you know? (I can easily see that 5/25 is greater than 3/25.)

As directed in Question 5B, ask students to write a fraction that represents the people that died in that age group.

Once students have written the common fraction, ask:

I see that 7/25 people died under the age of 9. What is the equivalent decimal fraction? (twenty-eight hundredths; 0.28)
How did you figure that out? (Possible responses: I know that decimals are fractions with denominators like 10 or 100 or 1000. 7/25 = ?/100. I know that 25 × 4 = 100 and 7 × 4 = 28. So 7/25 = 28/100 or 0.28.)
How did you choose the denominator? (Possible response: I chose 100 because I needed to find a fraction equivalent to twenty-fifths.)

Give students time to write the equivalent decimal fractions for the data. See Figure 2.

When most students are done, ask:

What does the decimal fraction mean? (Possible response: the number of people that died out of 100)

In Question 6, students are directed to organize the 2014 data as well. See Figure 3.

Use Data Tables to Describe the Life Span Data. In Question 7–15, students compare the life spans of the people in the data the boys collected. Organize students to discuss these questions and solutions with a partner. As students are working, circulate and identify the strategies students are using to compare the fractions, specifically in response to Questions 13–15. After most students have had a chance to work through these problems, organize students to discuss Questions 11–12.

Ask:

Look at the common fraction column. What is the sum of all the fractions in this column? (The sum is 1 or 25/25.)
What does this sum mean? (It represents the whole set data.)

Discuss Questions 13–15. Ask the identified students to share the strategies they used to answer these questions.

What strategy did you use? (Possible response: I looked at the decimals and estimated the sum; I looked at the fractions and estimated. I knew I needed to find half and half of 25 is 12.5.)
Who agrees with [student name]?
Did anyone use a different strategy?

Refer students to Question 16 and ask them to work with a partner to write a statement about the data sets. Direct students to record their statement on sentence strips or a sheet of paper that can be displayed with the other statements written by their classmates.

Ask:

What can you use to help you write a statement? (The statements in the previous questions can help me and the data tables can help me.)

Ask students to read their statement to another group of students. See Figure 4 for examples of statements.

Do you agree with the statement?
Why or why not?
What information from the data did you use?
Did anyone else write the same or similar statement?
Who would like to share a different statement?

Gather and display these statements with a completed data table and graph. Students will add statements later in the lesson. These should also remain on display through Lesson 6 to serve as models and examples.

Challenge students to write a good wrong statement about the data. A good wrong statement is A statement indicating that is close to true but is not true or is A statement indicating that represents a common error someone might make about the data.

Graph the Life Span Data. Looking at the numerical patterns in the data table is one way to represent the data. A graph is another. Give each student two copies of the Centimeter Grid Paper Master and refer them to Question 17. Use a display of the Centimeter Grid Paper Master to demonstrate how to scale and label the graph. Students are directed to make a bar graph for each data set. However, this graph will be somewhat different from other bar graphs they have made. Students will graph the Fraction of Deaths on the vertical axis. Make sure that students scale this axis appropriately so both graphs use the same scale. One suggestion is to scale by 0.4 intervals. The Age in Years will be graphed on the horizontal axis. The lines of the graph will be numbered using the first number of each interval. The spaces between the lines represent the bins or intervals. Students build the bars in these spaces to show that the data falls within the interval. See Figures 5 and 6. Circulate as students are making the graphs. Display the Graphing Life Spans Master to show examples of the completed graphs.

Use Graphs to Describe the Life Span Data. As students complete their graphs, ask them to discuss Questions 18 in a small group. Encourage students to connect the location and height of the bars of the graph to the data. For example, they can say that the tallest bar at the beginning of the graph tells us that many people in the 1858 data set died in early childhood.

Ask:

What true statement can you write from your descriptions of the graph? (See Figure 4 for some example statements. For example, most people died between the ages of 70 and 90 in 2014.)
What information did you use to make that statement? (Possible response: I see that the tallest bars and most of the data is in the 70 to 80 and 80 to 90 years old columns on the graph.)
The tallest bar in the 1858 graph tells us that the largest part of the people died before they were 10. Look at the data table. Do the numbers and patterns in the data table confirm the same description? (Possible response: Yes, the numbers and patterns in the data table show that the largest part, .28 or 28/100 of the people, died before they were 10 years of age.)

To make the discussion of Question 18 more efficient, ask half of the class to focus on the 1858 data and the half to focus on the 2014 data as they discuss the data in Question 18. Choose a student to help facilitate the discussion for each group and record ideas from the group on chart paper. Then each facilitator can present the ideas of the group in a whole class discussion.

Use Averages to Describe the Life Span Data. Using averages is another way to represent the data. Questions 19–20 ask students to estimate first the average life span and then find the median. Since half of the 1858 data falls within the first three bars, they can estimate that the average age at death is near 30 years old. Since most of the data is above 70 in the 2014 data, they can estimate the average age at death is around 80 years old. To find the median, students will need to order the ages from youngest to oldest and find the middle value.

Write statements using the averages and add them to the statements written and shared earlier with Question 18. See Figure 4 for possible statements.