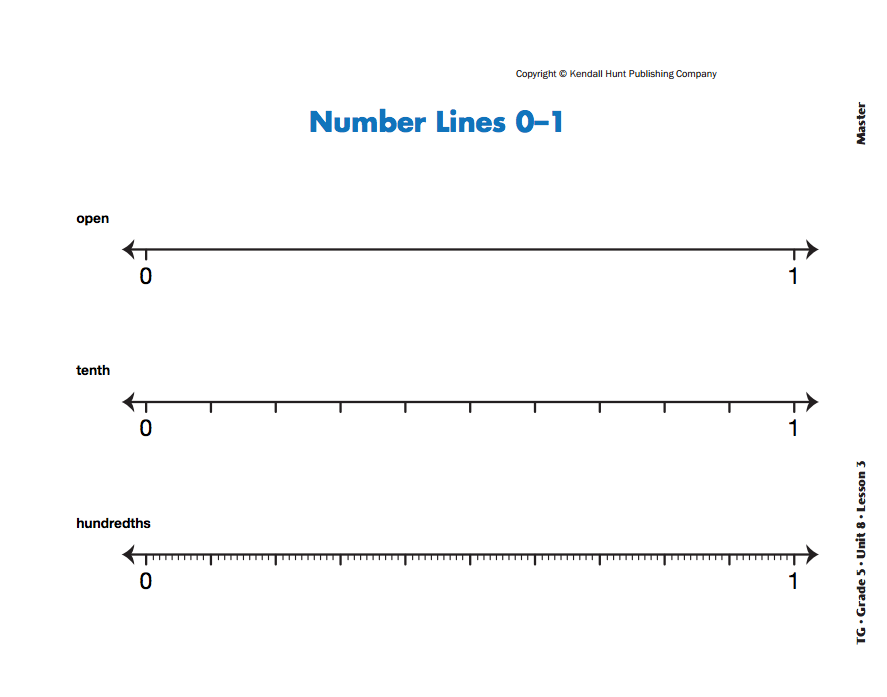
Estimate Hundredths on the Number Line. Begin the lesson using the display of the top number line on the Number Lines 0–1 Master.
- What are the endpoints for this number line?
(0 and 1)
Direct students to look at the number line and estimate where they would place 0.3 on the number line. Figure 1 shows a possible response.
Ask one student to come to the display and show an estimated location for 0.3.
After students have estimated a location for the decimal, ask:
- What strategy did you use to estimate the location of 0.3 on the number line? (Possible response: I know that 0.5 will be halfway between 0 and 1 and 0.3 is less than 0.5, so it will be somewhere between 0 and the halfway point [0.5] on the number line. I know it will be a little closer to 0.5 than it will be to 0.)
- What could you add to the number line to make it easier to locate 0.3 on the number line? (If you divided the line into tenths or ten equal sections you could more easily locate 0.3 on the line.)
Uncover the second number line on the display on the Number Lines 0–1 Master.
- How is this number line the same as the first one on the page? (It has the same endpoints of 0 and 1.)
- How is it different? (The second number line is divided into ten equal sections or tenths using hash marks.)
- If you start at zero and count each mark until you get to 1, what numbers will you say? (zero, one tenth, two tenths, three tenths, four tenths, five tenths, six tenths, seven tenths, eight tenths, nine tenths, one)
- What strategy can you use to find the location of 0.3 on this number line? (You can start at zero and count the marks on the number line to see where three tenths will be located.)
To decide if the estimate on the first number line was reasonable, compare the placement of 0.3 on the first
number line with the placement on the second number line.
- What strategy can you use to find the location of 0.35 on the number line? (Possible response: Each tenth of the number line is equal to ten hundredths. 0.35 will be halfway between 0.30 and 0.40 on this number line.)
- How can you use this strategy to estimate the location of 0.48 on this number line? (Possible response: 0.48 will be between 0.40 and 0.50 but it will be closer to 0.50 on the number line because forty-eight hundredths is almost to fifty hundredths.)
Ask a student to use a different color pen to locate 0.35 and 0.48 on the tenths number line on the displayed Master. Then reveal the number line divided into hundredths.
- What is different about this number line? (This number line is divided into hundredths. Each tenth is divided into ten parts.)
- Where is 0.35 on this number line? (0.35 is going to be between 0.3 and 0.4 and five hundredths to the right of 0.3.)
- Where is 0.48 on this number line? (0.48 is between 0.4 and 0.5 and is eight hundredths to the right of 0.4.)
- Look at where you placed 0.35 on the tenths number line and compare it to the actual location on the hundredths number line. How close was your estimate? (Possible response: I was off by 2 hundredths.)
- Look at where you placed 0.48 on the tenths number line and compare it to the actual location on the hundredths number line. How close was your estimate? (Possible response: I was off by 4 hundredths.)
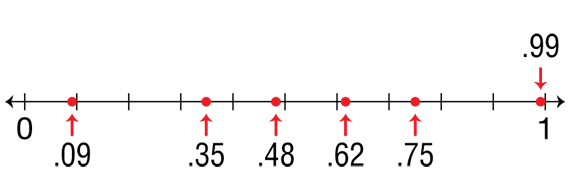
Continue to ask students to estimate the location of decimal numbers to the hundredths place. See a list of examples in Figure 2. Ask students to place the number on the tenths number line and then on the hundredths number line. Students should then determine the accuracy of the estimate.
Play Score One Game. Direct students to the Score One Game pages in the Student Activity Book. After students read the directions with their partner, provide time for them to prepare their list of decimals and play the game.
After students have had a chance to play the game at least one time, display the Number Lines 0–1 Master. Focus on the hundredths number line.
- What represents the whole? (the distance between zero and one on the number line)
- What represents one tenth? (the distance between the large marks)
- What represents one hundredth? (the distance between each small mark)
- How many hundredths are in one tenth? (ten)
- How many tenths are in one whole? (ten)
- Which is greater, a tenth or a hundredth? (tenth)
- How much greater is a tenth than a hundredth? (ten times greater)
Represent Decimals with Grids. To begin this part of the lesson, refer students to the Hundredths on Grids section of the Student Guide. Read the brief vignette introducing Frank's art project.
Before asking students to complete the table in Question 1, ask:
- When you look at Frank's art project, what represents the whole? (The total 10 × 10 square is one whole.)
- Into how many small squares is the whole divided? (100)
- What fraction of the whole is each small square? (1/100)
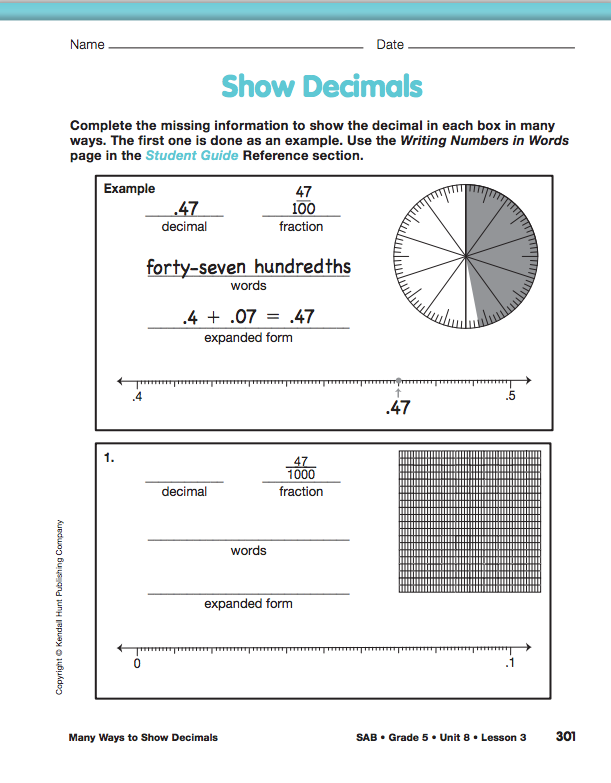
Ask students to complete and discuss Questions 1–2 with a partner. Refer students can use the Writing Numbers in Words page in the Student Guide Reference section if needed.
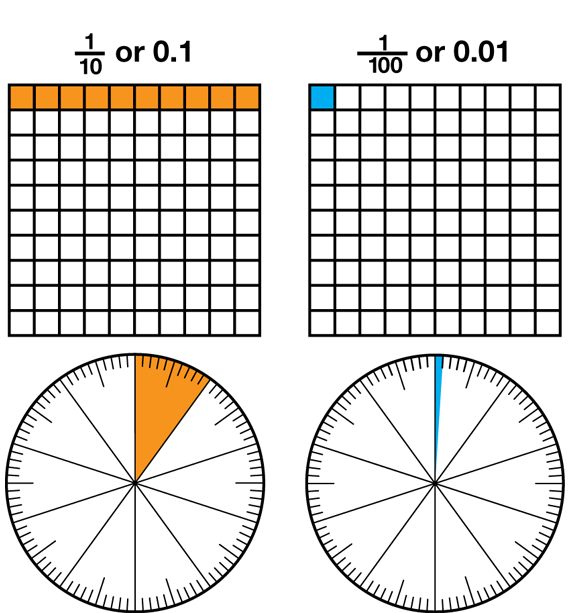
When most students have completed these two questions, discuss student's response to Question 2. Students should recognize that all of the representations are different ways to show what fraction of the grid was shaded. Ask students to use their Hundredths Circle Wheels to show 84/100.
- Look at the hundredths circle and the hundredths grid. How are they similar? (They are both area models, both areas are divided into 100 pieces.)
- How are they different? (The models are different shapes; the hundredths are organized into rows
on the grid rather than sections of a circle.)
- What does a tenth look like on each representation? (See Figure 3.)
- What does a hundredth look like on each representation? (See Figure 3.)
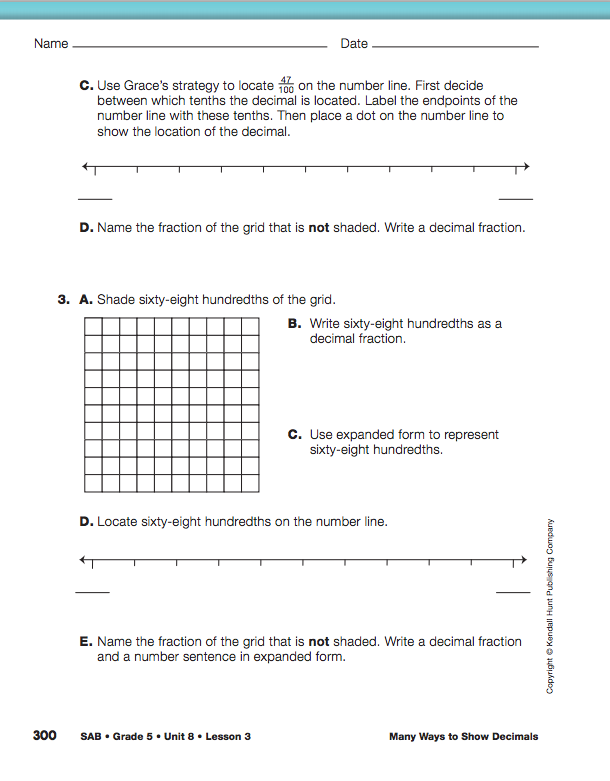
Ask students to turn to the Decimal Grids: Hundredths pages in the Student Activity Book. Display and ask students to complete Question 1. Ask a student to show their work on the display. Then direct students' attention to the vignette and number line after Question 1.
- What did Grace do to locate twenty-three hundredths on the number line? (She decided which two tenths 0.23 is between and labeled each benchmark. She knows there are 10 hundredths in a tenth. She then counted hundredths until she
located three hundredths.)
- What number is located at the first mark after 0.2? (0.21)
Finish counting and labeling the fractions at each of the other marks on the number line. Then ask students to complete Questions 2–3.
Once students have completed those problems, display and direct their attention to the Thousandths on Grids section of the Student Guide. Use Questions 3–7 to introduce students to representing decimals on the thousandths grid.
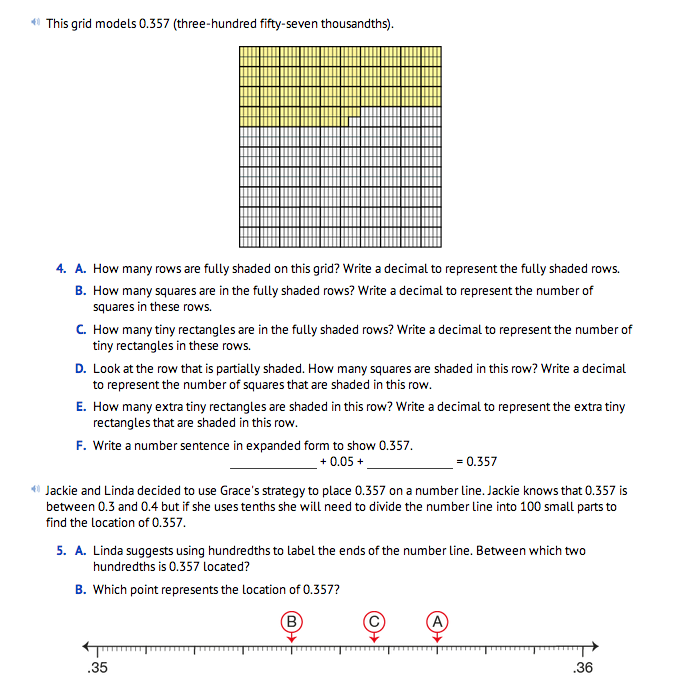
Use Question 3 to introduce students to this grid. Question 4 refers to a grid that represents 0.357. The first three rows on the grid are fully shaded. Each fully shaded row represents one tenth of the total square so the three rows represents 0.3 (3/10) of the square. Since each row is divided into 10 small squares, three rows represents 0.30 (3/100) of the total square. This area also represents 300 tiny rectangles or 0.300 (300/1000) of the total grid. In the fourth row there are 5 small squares or 0.05 (5/100) shaded. Finally, in the fourth row, there are 7 extra tiny rectangles shaded or 0.007 (7/1000) shaded. To express this using expanded form students write: 0.3 + 0.05 + 0.007 = 0.357.

There are two ways to read the decimal number 0.357.
- Read the number after the decimal point as a whole number and give it the name of its last decimal place. Read 0.357 as ”three hundred fifty-seven thousandths.”
- Read it as “point three-five-seven.”
The first option is preferred at this time because it reinforces a knowledge of the place value system.
Decimals are often written with a leading zero that does not change the value of the number. For example, either 0.4 or .4 can represent four-tenths.
To answer Question 5, students extend their understanding of place value to recognize that 0.357 is between 0.35 and 0.36. They then use this understanding to place 0.357 on a number line. In Question 5B, students are asked to locate 0.357 by choosing from three labeled points.
- Which point represents the location of 0.357?
(Point A)
- What number is located at Point B? (0.354 or three-hundred fifty-four thousandths)
- What number is located at Point C? (0.3557 or three-thousand five-hundred fifty-seven ten-thousandths)
- What do the small marks on Linda's number line represent? (one ten-thousandth)
Display the Decimal Number Lines Display Master. Cover the top number line and show the bottom number line. Label the ends of the number line with 0.3 and 0.4. See Figure 4.
- Where is 0.357 located on this number line? (See Figure 4.)
- What numbers are located at the large marks on the number lines? (See Figure 4.)
- Compare this location to where 0.357 is located on the Linda's number line in Question 5? Why are
the numbers in different locations? (See Figure 4 and Figure 5. Because the benchmarks changed, the meaning of the marks on the number line changed.)
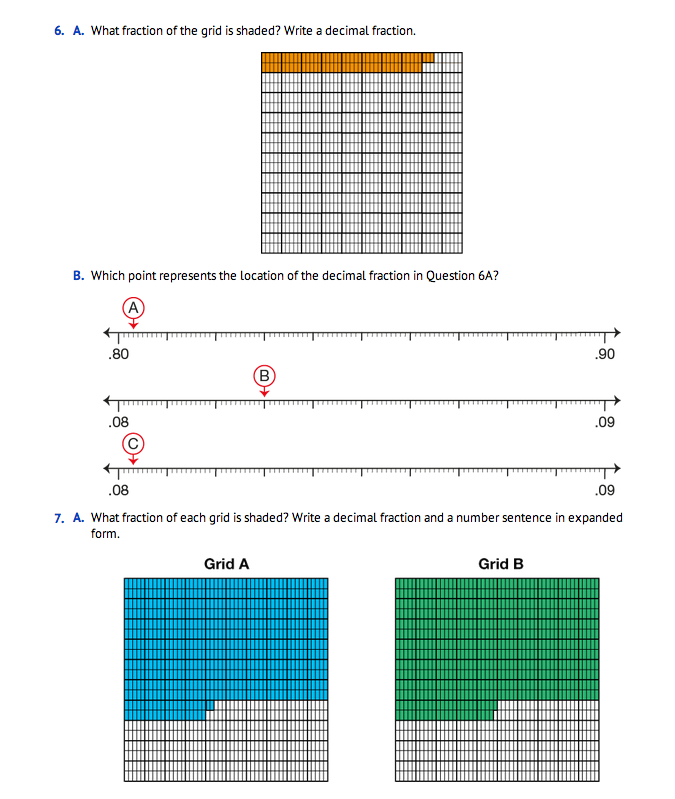
Display the number lines in Question 6B in the Student Guide.
- Which point represents the location of the decimal fraction .083? (Point B)
- What is the distance between .08 and .09? (one-hundredth)
- What number is located at Point A? (0.83 or eighty-three hundredths)
- What is the distance between 0.80 and 0.90? (one-tenth)
- What number is located at Point C? (.0803 or eight hundred three ten-thousandths)
- What is the distance between .08 and .09? (one hundredth)
Display the grids in and discuss Question 7.
- Look at the number lines in Question 7C. Which locations are correct? (Both number lines show
the corrections of the decimals represented in Question 7A.)
- What is different about the number lines? (Each shows a different pair of benchmarks.)
- Look at the number line with 0.6 and 0.7 as benchmarks. What numbers are located on the large marks? (0.61, 0.62, 0.63, 0.64 . . . . .0.69, 0.70)
- What do the small marks on this number line represent? (one thousandth or 0.601, 0.602)
- Look at the number line with .64 and .65 as benchmarks. What numbers are located on the large marks? (0.641, 0.642, . . . 0.649)
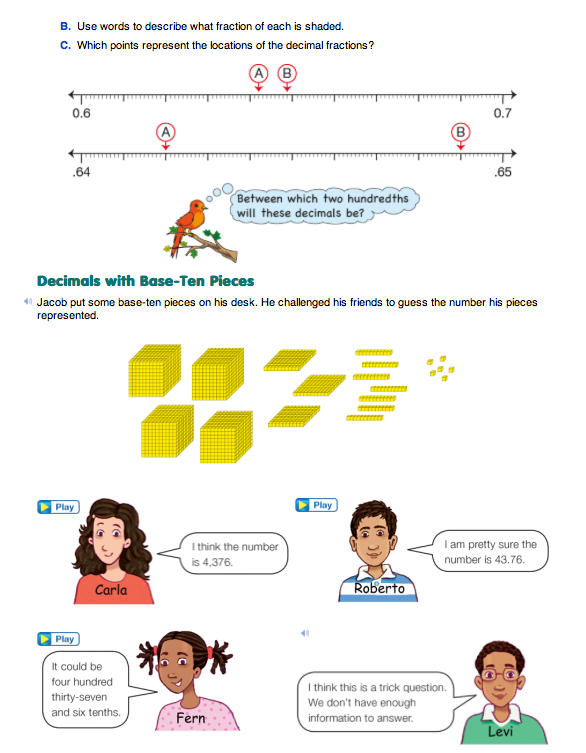
Represent Decimals with Base-Ten Pieces. Direct students to the Decimals with Base-Ten Pieces section in the Student Guide. Ask them to read the vignette describing Jacob's challenge and to think about the responses given by each student on the page.
- Why do you think Carla, Roberto, and Fern each thought that Jacob's base-ten pieces represented a different number? (Possible response: Roberto and Fern each thought the number could have a decimal point in it and Carla just thought about the base-ten pieces representing a whole number.)
- What information does Levi think may be missing? (Possible responses: Levi wants to know if there is a decimal point as part of this number; he wants to know the value of a bit.)
- If Jacob told his friends that his number was between 1 and 5, how would that help them decide what number the base-ten pieces represent? (Possible response: They would know that the packs represent the digit in the ones place and all the other base-ten pieces would represent digits to the right of the decimal point. The number would be 4.376.)
- If Jacob said his number was between 100 and 500, what number would the base-ten pieces represent? (437.6) Which base-ten piece would represent the ones place or the whole in this number? (The skinnies represent one or the whole.)
- In Carla's guess, which base-ten piece did she think represented the ones place or the unit whole? (the bit)
- Why is it important to know which base-ten piece represents the unit whole when you are using them to model numbers? (Possible response: so you will know if the number you are representing has a decimal point and digit to the right of the decimal place)
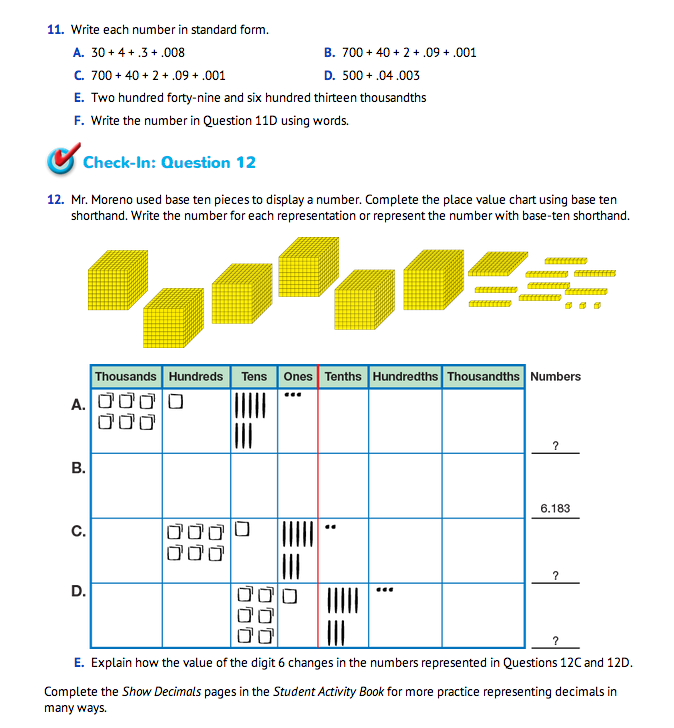
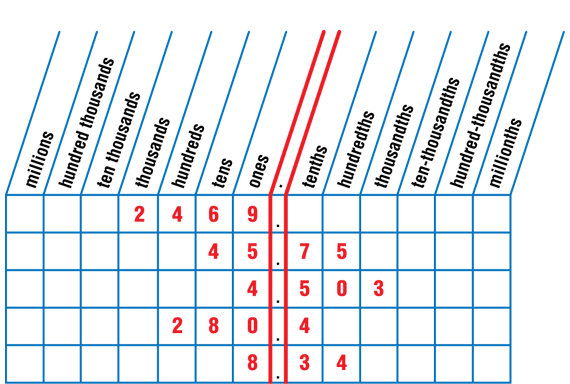
Students work with their partner and use base-ten pieces or base-ten shorthand to model the numbers in Question 8. As each number is modeled, ask someone to read the number and to identify which base-ten piece represents the ones place or the unit whole for each number. To complete Question 8F, students will need to identify the value of the digit 4 in each number they just modeled and describe how the value changes in each number. To help students see how the value changes, record the value of the 4 in each number using a display of the Decimal Place Value Chart Master. See Figure 6.
As students look at the place value chart, ask them to describe what they notice. Students should recognize that each time you move one place to the left on the place value chart the value of the 4 is ten times greater than the place to its left. Conversely, each time you move one place to the right on the chart the value of the 4 is ten times less than the place to its left.
In Question 9, students connect the place value chart and base ten representations to expanded form. Students can complete Questions 10–11 for additional practice representing decimals using expanded form and standard form.
Ask students can complete Check-In: Question 12 independently or with a partner.
Use Check-In: Question 12 in the Student Guide to assess students' abilities to represent numbers to the thousandths place using symbols, words, and base-ten pieces [E1]; make connections among representations [E2]; and recognize that in a multidigit number, the value of a digit in one place is ten times greater than it represents in the place to its right and 1/10 as great as it represents in the place to its left [E5].
The Score One Game in the Student Activity Book can be used to provide targeted practice.
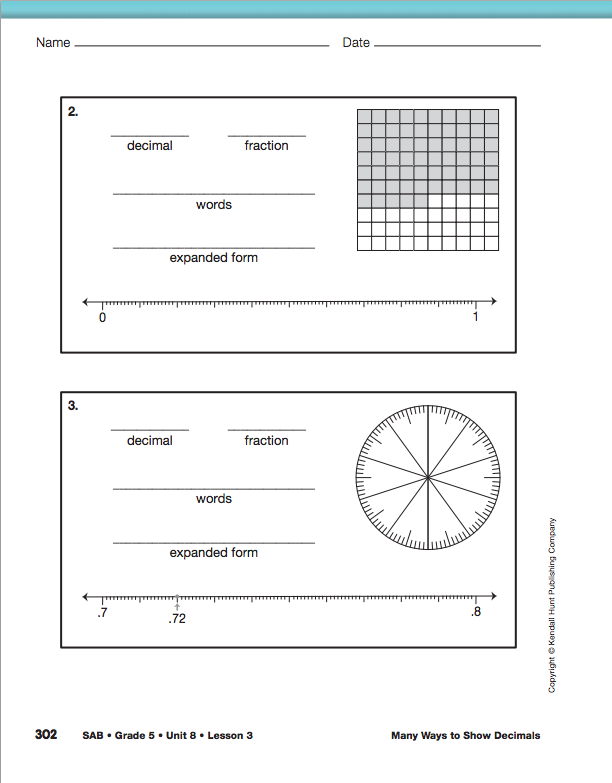
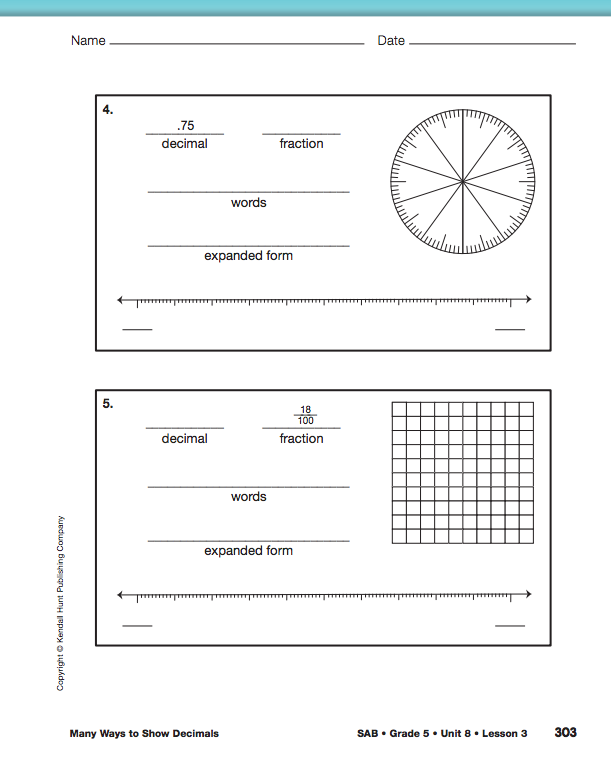
Ask students to complete the Show Decimals pages in the Student Activity Book to continue to practice representing decimals using multiple representations.
Use the Show Decimals pages in the Student Activity Book to assess students' abilities to
represent numbers to the thousandths place using symbols, words, and base-ten pieces [E1]; make connections among representations [E2]; and recognize that in a multidigit number, the value of a digit in one place is ten times greater than it represents in the place to its right and 1/10 as great as it represents in the place to its left [E5].
The Score One Game in the Student Activity Book can be used to provide targeted practice.
To provided targeted practice with representing decimals on number lines, provide students copies of the Decimal Number Lines Master and ask them to represent various decimal fractions.