Use Invented Strategies to Multiply. Estimation must play an important role in developing a multiplication algorithm. With a strong understanding of place value, students will be able to use paper-and-pencil multiplication procedures they are comfortable with and then place the decimal in its correct place within the product. Even if they understand how to “count the number of places behind the decimals in the factors,” in order to place the decimal in a product, students can make mistakes if they don't estimate. The multiplication of two numbers will produce the same digits, regardless of the positions of the decimal point, for example, 12 × 12 = 144 and 1.2 × 1.2 = 1.44. Because of this, students can simply ignore the decimal, multiply the two numbers as whole numbers, and then use estimation to place the decimal within the product. Begin the lesson by allowing students to find invented strategies with which to multiply a decimal by a whole number.
Direct students to the Strategies for Multiplying Decimals pages in the Student Guide.
Start the lesson with the word problem on the page:
Encourage students to use invented strategies to find the exact answer to 3 × 4.5. They can use tools such as tenths grids, base-ten pieces, and fraction circle pieces. Students will need to combine their fraction circle pieces or base-ten pieces, or use sketches of the tools in order to have enough to represent 13.5. Have copies of the Tenths Grids Master available for student use. Students who choose to solve the problem using tenths grids will need 14 tenths grids to represent the problem.
Before discussing students' solutions, ask student volunteers to model the problem:
- Who would like to show how to model 3 × 4.5 with base-ten pieces or shorthand? (See Figure 1.)
- Who would like to sketch fraction circle pieces to model the problem? (See Figure 2.)
Next, discuss students' solution strategies. Some students may use repeated addition, 4.5 + 4.5 + 4.5 = 13.5. Others may multiply the whole numbers 3 × 4, multiply 3 × 1/2, and then add the products together, (3 × 4) + (3 × 1/2) - 131/2. Other students may multiply 3 × 4 and then add on .5 + .5 + .5.
Explore Multiplication Patterns. Assign Questions 2–5 to student pairs. Discuss the patterns students see when multiplying a number by a ten. Write any problems you discuss on the board so that students can clearly see how the decimal points move in multiplication problems.
- What happens when you multiply a whole number by 10? (It gets 10 times larger. You add a zero to the end of the whole number.)
- What happens when you multiply a whole number by 100? 1000? 10,000? (It gets 100, 1000, or 10,000 times larger.)
- What is your rule for multiplying a number by tens (Question 3)? (Possible response: To multiply numbers that end in zero, you just multiply the numbers without the zeros on the ends, and then put as many more zeros on the end of the product as there are in the numbers.)
- Why does this rule work? (Because if you multiply a number by ten, you are making it ten times bigger. Adding a zero on to the end shows it is ten times bigger. For example, 3.0 × 10 = 30. If you multiply a number by 100, you are making it 100 times bigger. Adding two zeros on to the end shows that is it 100 times bigger. For example, 3.0 × 100 = 300. You need to add the zeros in and move the decimal point to the right.)
- Where is the decimal point placed in a whole number? (after the unit whole; For example, in 36, the decimal goes after the 6.)
- Is 36.0 the same as 36? (yes)
- What is 36.0 × 10 (Question 2B)? (360.0)
- How does the decimal move? (It moves one place to the right.)
- What does moving the decimal one place to the right show? (It shows the product is ten times bigger.)
- Does the decimal point move if you multiply a number by 1? (no)
Continue discussing students' responses to Questions 4–5.
- For the problems in Question 4, how did estimating help you find the correct answer? (Possible response: If I just multiplied the whole numbers, it gave me an idea of where the decimal point should be placed in the product.)
- Choose a problem and explain how you estimated the product.
- What is 3.6 × 10 (Question 4B)? (36.0)
- What happens to the decimal point? (It moves one place to the right.)
- What does this show? (that 36 is ten times bigger than 3.6)
- What is one-tenth of 36? (3.6 is one-tenth of 36.)
- What is 3.6 × 10,000 (Question 4E)? (36,000.0)
- How did estimation help you know that that answer was reasonable? (Possible response: 3 × 10,000 is 30,000 so I know it had to be around 30,000.)
- How many places did the decimal point move? (4 places to the right)
- What does moving the decimal four places to the right show? How many times larger is 36,000.0
than 3.6? (It shows that 36,000.0 is 10,000 times larger than 3.6.)
- Explain your rule for multiplying a decimal by a multiple of ten (Question 5B). Does it relate to your rule for multiplying whole numbers by tens in Question 3? (Possible response: They are similar.
When I multiplied a whole number by a ten like 100, I wrote two zeros at the end of the product to show the product was 100 times bigger. When I multiplied a decimal by a ten like 100, I move the decimal two place to the right to show that it is 100 times bigger.)
- How would a decimal point move to make the product smaller? (to the left)
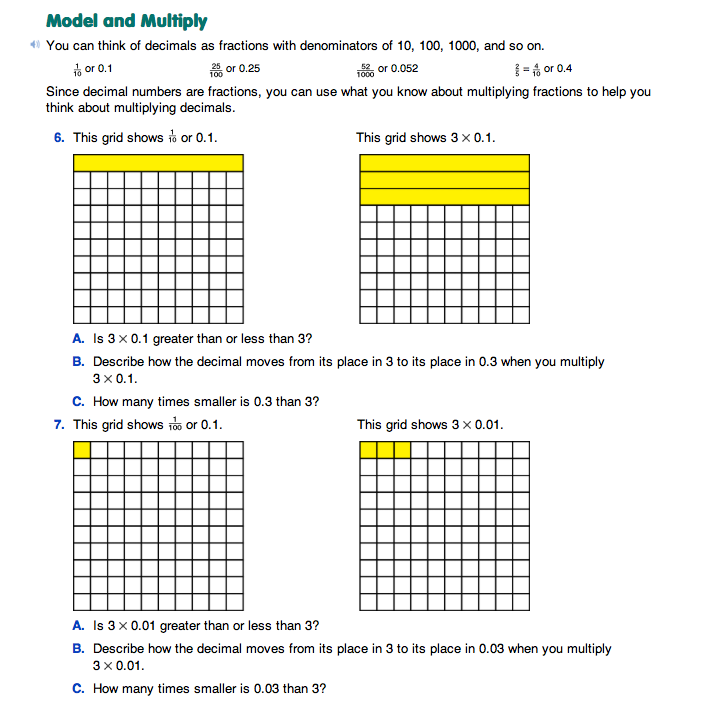
Model and Multiply. Read the Model and Multiply section in the Student Guide and complete Questions 6–7 together as a class. Use display base-ten pieces to model the problems as shown in the text. Discuss how the product will be smaller than the whole number factor when you multiply it by a decimal less than 1 (e.g., 3 × 0.1 = 0.3 and 3 × 0.01 = 0.03). Discuss how the decimal is moved to the left one place to show that the product 0.3 is 10 times smaller than 3 in Question 6, and two places to the left to show that 0.03 is 100 times smaller than 3 in Question 7.
Continue to discuss place value. Review that in a multidigit number, a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left.
- How is 4 related to 40? (4 is 10 times smaller than 40, or one-tenth of 40 is 4.)
- How is 400 related to 4000? (400 is 10 times smaller than 4000.)
- How is 300 related to 3000? (300 is 10 times smaller than 3000.)
- How is 500 related to 50? (500 is 10 times larger than 50, or 50 is one-tenth as large as 500.)
- Where is the decimal point placed in a whole number? (after the unit whole; For example, in 36, the decimal goes after the 6.)
- Work with a partner to find some factors of 120. Find several pairs. (Possible responses: 40 × 3, 30 × 4, 20 × 6, 60 × 2, 12 × 10, 10 × 20)
After students have found several factor pairs, use the factors 40 × 3 as an example as you have the following discussion.
- How can you adjust the place values of 40 or 3 to get a smaller product? (Move the decimals to the left.)
- Using the factors 40 and 3, work with your partner to find a pair of numbers whose product is 12.0? (4 × 3)
- How many times smaller must one of the numbers be to give the new product? (One of the numbers has to be 10 times smaller.)
- Using the same factors, adjust the place values to find a pair of numbers whose product is 1.20 (0.4 × 3 or 4 × 0.3)
- How about 0.120? (0.3 × 0.4)
- If multiplying a number by 10 makes a number 10 times larger, how do you make a number 10 times smaller? (Multiply it by one-tenth.)
- How do you make a number 100 times smaller? (Multiply it by one-hundredth.)
Use Patterns and Estimation to Place the Decimal. Assign Question 8–13.
Upon completion, discuss students' responses:
- What happens to the decimal point as you multiply a number by one-tenth? (The decimal moves to the left.)
- What happens to the decimal point as you multiply a number by one-hundredth? By one-thousandth?
By one-ten thousandth? (moves 2 places to the left; 3 places to the left; 4 places to the left)
- Does that show that the product is getting larger or smaller? (smaller)
- What did you notice about the products in Question 10? (All of the products contain the same digits. The only thing that changes is where the decimal is placed.)
- How did you estimate 12 × 1.2, and how did that help you place the decimal point? (Possible response: I knew it would be more than 12 × 1, but less than 12 × 2, so the decimal point had to go after the 14.)
- Is 12 × 1.2 less than or greater than 12 × 0.12? How do you know? (greater than; 1.2 is greater than 0.12.)
- How did you estimate the product of 12 × 0.12? (Possible response: I thought of 12 times one-tenth or twelve-tenths. Ten-tenths is one, so I knew it would be around 1.)
List the numbers 12, 1.2, 0.12, 0.012, and 0.0012 on the board.
- Look at the numbers you multiplied by 12. What do you notice? How do they relate to one another?
(Each number is a tenth smaller than the number before it.)
- As you multiply 12 by numbers that decrease by a tenth, what happens to the products? (The products decrease by one-tenth each time, too.)
List the products for the problems in Question 10 on the board: 144, 14.4, 1.44, 0.144, and 0.0144.
- How much smaller is 14.4 than 144? How do you know? (ten times smaller; The decimal moves one place to the left from 144 to 14.4 so I know it is 10 times smaller.)
- How much larger is 14.4 than 1.44? How do you know? (ten times larger; The decimal moves one place to the right from 1.44 to 14.4 so I know 14. 4 is 10 times larger.)
- How much larger is 144 than 1.44? How do you know that is reasonable? (100 times larger; Possible response: It is reasonable to think that 144 is 100 times 1.44 because 1.44 is close to 1, and 144 is close to 100.)
- What happens to the decimal point as you multiply a number by 10? (moves to the right 1 place)
- What happens to the decimal point as you multiply a decimal number by 100? By 1000? (moves to the right 2 places; 3 places)
- Can you predict the size of the product? Use the problems in Questions 12–13 to help explain.
(Possible response: If I multiply a whole number times a decimal less than 1, the product is smaller than the whole number, like 25 × 0.01. If I multiply a decimal by a ten, it gets bigger, like 2.5 × 100.)
- If you multiply a decimal times a decimal, what do you predict the size of the product will be? (Possible response: smaller than each of the factors)
Assign Check-In: Questions 14–17. Students will multiply decimals by whole numbers and use patterns and estimation to help them place decimals. Students will explain that a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left, and the patterns in the placement of the decimal point when a decimal is multiplied or divided by a power of ten.

Use Check-In: Questions 14–17 on the Strategies for Multiplying Decimals pages in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to recognize that a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left [E5]; and explain the patterns in the number of zeros of the product when multiplying by a number by powers of 10, and explain patterns in the placement of the decimal point when a decimal is multiplied or divided by a power of ten [E6].
Use Rectangle Models. Read the short vignette about Mr. Moreno's pieces of tape and discuss the rectangle model used to solve 3 × 2.2 meters. Ask students to compare the partial products 3 × 2 and 3 × 0.2 as shown in Nicholas's rectangle model. Students should notice that 3 × 0.2 = 0.6 is ten times smaller than 3 × 2 = 6. Assign Questions 18 so that students can practice using rectangle models to multiply a whole number by a decimal.
Assign Home Practice Part 9 as homework.