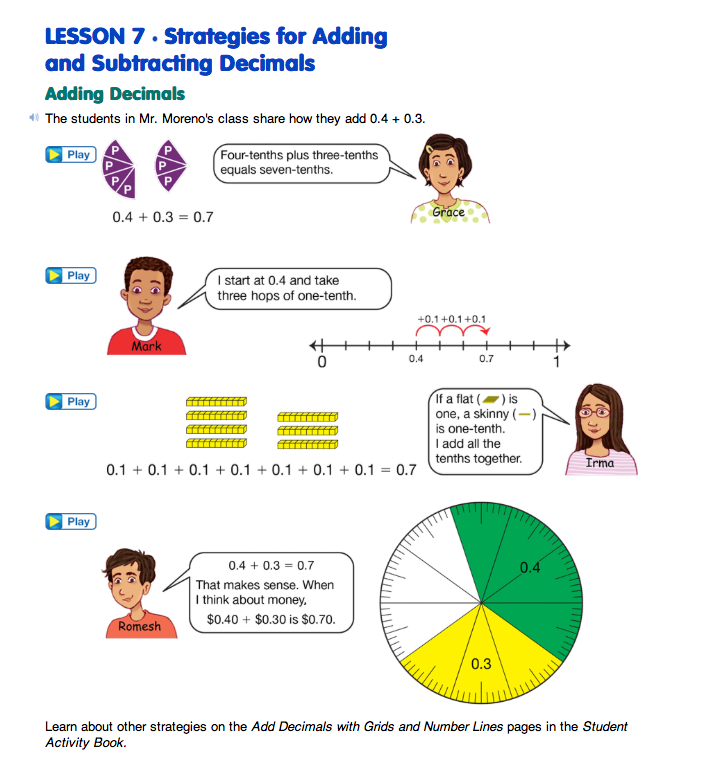
Add with Patterns on Number Lines. Display the Number Line Patterns 1 Master and direct students' attention to the first number line. Ask students to find the next three numbers in the sequence 0.5, 1.0, 1.5, 2.0, 2.5. Have students describe the pattern that helped them determine the next numbers in the sequence. Students should see that the pattern is adding 0.5. Then ask a volunteer to write the answers 3.0, 3.5, and 4.0 in their approximate places on the number line, explaining why they placed the numbers where they did. Repeat the process for the remaining three number lines.
Invent Strategies. Begin this part of the lesson by allowing students to invent and explore methods for adding simple decimal numbers. Encourage students to use a range of conceptual representations to find sums and differences with decimals before introducing more formal numerical algorithms. Each representation solidifies and deepens students' conceptual foundations about operations with decimal numbers and will help them bring number sense into increasingly complex computations in the future. Use displays of the Decimal Number Lines, Decimal Grids, and Hundredths Circles Masters as needed throughout the discussion. Display the following number sentence vertically:
- How would you estimate this sum? (Possible response: 0.4 is close to 0.5, which is the same as one-half. One-half and one-half is a whole, so I estimate the sum will be just under 1.)
- Who can think of a way to find the exact sum? Think about the tools you have been working with such as number lines, base-ten pieces, fraction circle pieces, and hundredths circles. (Possible response: You could start at 0.4 on the number line and hop another 0.4 to 0.8.)
Display the following number sentence vertically:
- How would you estimate this sum? (Possible response: Since I know 0.4 + 0.4 = 0.8, 0.4 + 0.3 will be just a little less than 0.4 + 0.4.)
- Who can think of a way to find the exact sum? (Possible response: You could use fraction circle pieces. Each purple piece is one-tenth of the red circle. 4 purples and 3 purples is 7 purples, seven-tenths.)
Display and direct students' attention to the Adding Decimals section of the Strategies for Adding and Subtracting Decimals pages in the Student Guide. Discuss the various strategies for adding decimals as presented on the page by asking students to explain how fraction circle pieces, number lines, and baseten pieces are used to add 0.4 + 0.3.
Use Models to Add. Next have student pairs complete Question 1 on the Add Decimals with Grids and Number Lines pages in the Student Activity Book. Students solve 0.4 + 0.3 again, this time using an area model, the hundredths grid.
When they have completed the question, ask:
- Did Irma meet her coach's requirement (Questions 1C and 1E)? (She didn't meet her coach's requirement when she just rode 0.4 + 0.3 miles. She does by riding 0.7 + 0.7 miles round trip.)
- How did you shade 0.4 of the grid? (I shaded four rows of ten.)
- How did you add 0.3 more? (I shaded three more rows.)
- How many rows are shaded? (7 rows)
- What decimal is represented? (0.7)
- Who would like to demonstrate how to use a number line to add 0.7 + 0.7 (Question 1D)? (Start at 0.7 and take 7 one-tenth hops to 1.4.)
- Show how to solve 0.7 + 0.7 with fraction circle pieces. (7 purples and 7 purples make 1 whole
red circle and 4 purple tenths more.)
Assign Question 2 to student pairs. Students estimate the sum of 0.25 + 0.4 and then use a hundredths grid to add. Upon completion, display the problem vertically. Emphasize the need to write the problem with the tenths aligned. Look for an understanding of the need to add like place values.
- Explain how to estimate the sum of 0.25 + 0.4. (Possible response: I know 0.25 is close to 0.3, so my estimate would be about 0.3 plus 0.4 or 0.7.)
- How did you show 0.25 on the grid? (I shaded 2 rows of 10 squares and then 5 more squares in the next row.)
- What do two shaded rows on the hundredths grid represent? (two-tenths)
- What do the 5 shaded squares on the hundredths grid represent? (five-hundredths)
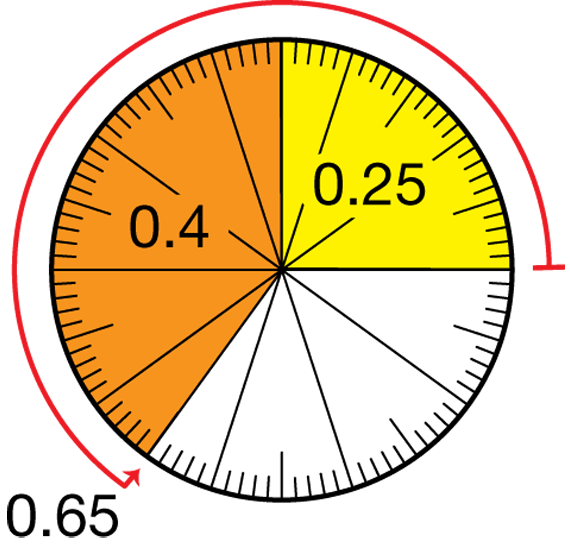
- How did you use the grid to find the sum of 0.25 + 0.4? (See Figure 1. Possible response: I shaded 2 whole rows and another half of a row. Then I shaded 4 more rows. In total, 6 shaded rows show six-tenths plus five-hundredths more for the half row of 5 shaded squares. That's 0.65.)
- Who would like to show how to use a hundredths circle to add 0.25 to 0.4? (See Figure 2.)
- How can you use base-ten pieces to add 0.25 + 0.4? The unit whole is a flat. (2 skinnies and 5 bits combined with 4 skinnies is 6 skinnies and 5 bits, or 0.65.)
Assign Questions 3–10 to student pairs. Students will use hundredths grids and number lines to add decimals. In Question 3, they must add 0.8 mile and 0.6 mile. Solving the problem with grids shows that the sum is 1.4 miles. Using estimation and an area model helps students avoid the common mistake of reporting the sum of 0.8 and 0.6 as 0.14.
Discuss Addition Strategies. Upon completion, discuss Questions 3, 5–6, and 8. Display the equations you are discussing vertically. Carefully align the place values so students begin to see that when adding decimals, they add the digits in the same places, just as with adding whole numbers.
- Is the sum of 0.8 + 0.6 greater or less than 1? How do you know? (Possible response: Greater than 1; 0.8 is greater than 1/2, and 0.6 is greater than 1/2 so combined they will be more than 1.)
- How did you use the grids to help you find the exact sum of 0.8 + 0.6 (Question 3)? (Possible response: I shaded in 8 rows on one grid, then split the six-tenths into two-tenths and fourtenths. I had 1 whole grid and four-tenths of another grid shaded, or 1.4.)
- How did you estimate the sum of 0.45 + 0.47 (Question 5)? (Possible response: I thought about money. $.45 and $.47 are both close to $.50, so I estimated a sum of a little less than $1.00 or 1.)
- Show how to use a hundredths grid to solve 0.45 + 0.47. (Shade in 4 rows plus 5 more squares. Then shade 4 rows and 7 more squares. There are 9 rows and 2 squares shaded in total. The sum is 0.92.)
- What common fraction represents 9 shaded rows on the hundredth grid? (9/10)
- What decimal fraction represents 9 shaded rows? (0.9)
- What common fraction represents 2 shaded
squares on the hundredths grid? (2/100)
- What decimal fraction represents 2 shaded squares? (0.02)
- Is 9/10 + 2/100 the same as 0.92? (yes)
- Show how to use a number line to solve 0.45 + 0.47 (Question 6). (Possible response: See Figure 3. I thought about breaking the numbers apart into tenths and hundredths. I started at 0 on the number line. I took 4 tenth hops and then 4 more tenth hops to add the tenths together, 0.8. I had 0.05 and 0.07 to still add on. I hopped in between 0.8 and 0.9 to add on 0.05. I hopped to 0.9 to add 0.05 more and then 0.02 to add 0.07. I landed on 0.92.)
- Did anyone use the number line a different way? (Possible response: I know there are 10 one-hundredth hops in between each one-tenth hop on the number line. I started at 0.45 and took 5 one-tenth hops forward. That was too much, so I hopped back 3 one-hundredth hops.)
- How do you know that a solution of 0.92 is reasonable? (Possible response: 0.92 is close to 1, and I estimated that the sum would be a little less than 1.)
As you discuss Question 8, talk about regrouping across a decimal. Explain that the tenths place cannot reflect more than 9 tenths. When they model 0.3 + 0.87 on grids, students should see that 3 tenths plus 8 tenths yields 11 tenths or 1.1, not 0.11. The remaining 7 hundredths results in a sum of 1.17.
- How is 1.1 different from 0.11? (1.1 means 1 whole and 1 tenth. 0.11 means 1 tenth and 1 hundredth. It is less than 1 whole.)
- What does 1.17 look like on a grid (Question 8)? (1 whole grid plus another row and 7 more squares shaded)
- How can you use base-ten pieces to model and solve 0.3 + 0.87? (3 skinnies plus 8 skinnies and 7 bits is 11 skinnies and 7 bits. The 11 skinnies make 1 flat and 1 skinny, so I have 1 flat, 1 skinny, and 7 bits or 1.17.)
Assign the Homework section of the Add Decimals with Grids and Number Lines pages in the Student Activity Book.