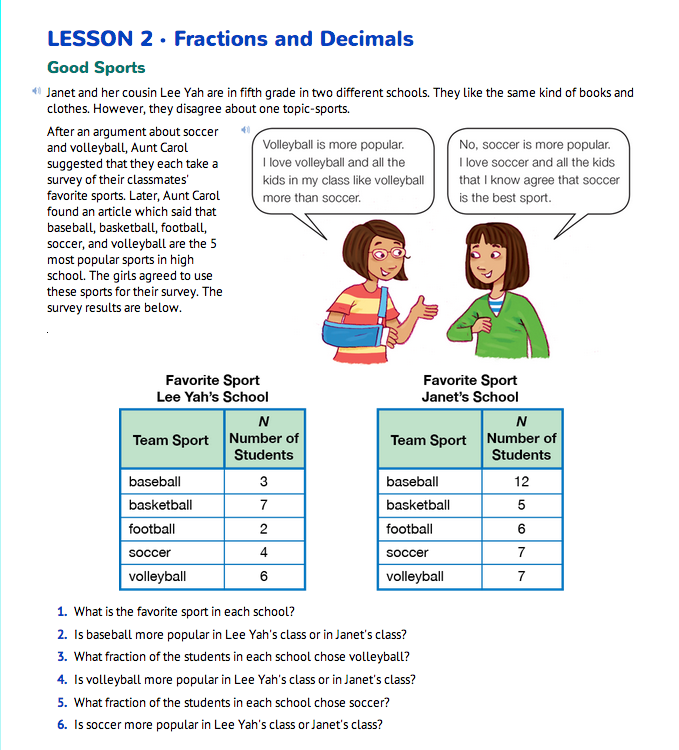
Analyze the Survey Data. Read the vignette in the Good Sports section of the Fractions and Decimals pages in the Student Guide. Lee Yah and her cousin, Janet, are trying to decide which sport is more popular: volleyball or soccer. Each girl surveys the fifth-graders in her school and students help them analyze the data
in Questions 1–6. Ask students to discuss Questions 1–6 with a partner.
After students have had a chance to get to know the data, ask:
- How did you decide if baseball was more popular in Lee Yah's class or Janet's class? (Possible response: I can see that only 3 people chose baseball in Lee Yah's school and people chose baseball the most often in Janet's class. So, baseball is clearly more popular in Janet's school.)
- How did you decide if volleyball was more popular in Lee Yah's class or Janet's class? (See Figure 1 for some possible responses.)
- How did you decide if soccer was more popular in Lee Yah's class or Janet's class? (Possible response: I cannot tell because the relationships between the numerator and denominator are not obvious.)
Accept any and all student ideas. Students will have a variety of ideas but will come to the conclusion that fractions that do not have common denominators can be more challenging to compare. Read the vignette before Question 7.
- What are Lee Yah and Janet doing to compare the fractions? (Each girl finds friendly numbers and tries to use equivalent fractions to compare the fractions. Both fractions are close to 1/5, so this does not help.)
Students can leave this problem with questions and some confusion as it will be revisited later in the lesson.
Represent Decimals with Circle Pieces. Distribute sets of fraction circle pieces and ask students to discuss Question 8 with a partner.
After students have had a chance to explore the problem, ask:
- How did you name the fraction Jessie is showing? (Possible response: I looked for a way to show the
same fraction with one color. The tenths worked. There are 9/10 showing.)
- What does it mean to write a decimal fraction? (Write the same fraction but as a decimal. 9/10 can also be written as 0.9 or nine tenths.)
- Look at 0.9 and 0.7. How do you know 0.9 is greater? (Possible response: I pictured 9 purple pieces and compared that to 7 purple pieces; or I know .90 of a dollar is more than .70 of a dollar; or I remember using base-ten pieces to show decimals. If the flat is the whole, 9 skinnies = 0.9. and 9 skinnies is greater than 7 skinnies.)

Fractions and Decimals. A fraction is a number that can be written as a/b where a and b are whole numbers and b is not zero. Using this definition both 5/10 and 0.5 are fractions because they both can be written as 5/10. We call 5/10 a common fraction and 0.5 a decimal fraction. The terms common fraction and decimal fraction are used in the Student Guide to emphasize that both notations can represent the same quantity. However, we usually refer to common fractions as just “fractions” and decimal fractions as just “decimals.”
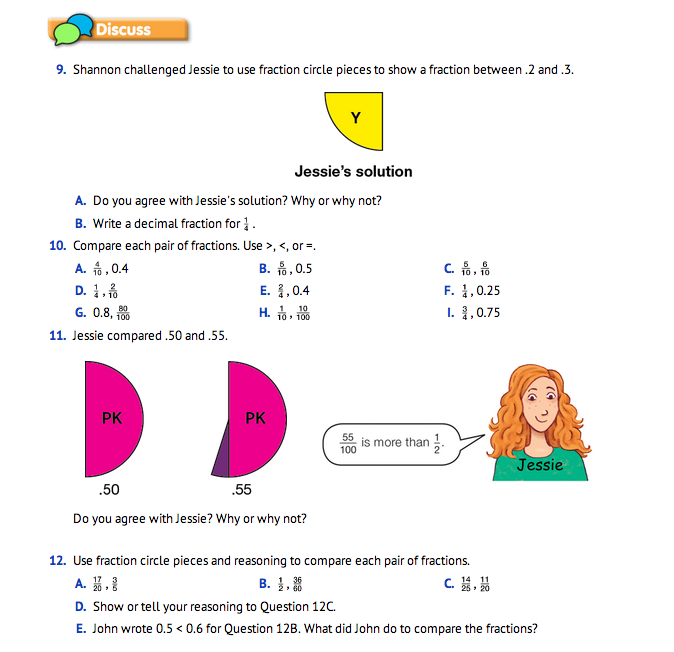
Read Question 9 aloud and ask students to discuss their solution with a neighbor for a few minutes.
- If the red circle is a whole, what does .2 look like?
(2/10 or 2 purple pieces)
- If the red circle is a whole, what does .3 look like?
(3/10 or 3 purple pieces)
- Is one yellow piece between .2 and .3? (yes)
- Are there any other fractions between .2 and .3 that you can show with your fraction circle pieces? (No, all others are either equivalent to 2/10, 3/10, or 1/4.)
- How did you decide what to write for the decimal fraction in Question 9B? (Possible response: I covered one yellow with purple pieces and it took 2 tenths and 1/2 of a tenth or 5/100. I wrote 0.25; I thought of the problem like money. I know 1/4 of a dollar is a quarter and a quarter is written as 0.25.)
Ask students to use their fraction circle pieces and reasoning to compare the fractions in Question 10. As students are working, circulate and ask students to show you how they solved some of the problems. Observe and make note of the strategies students are using to compare the fractions. Most of the fractions in Question 10 are frequently discussed or are often used as benchmarks.
Direct students' attention to Question 11 and ask:
- Who does not agree with Jessie?
- Why not?
- Who agrees with Jessie?
- Why? (Possible response: I think her model is correct. 0.55 is 5/100 greater than 1/2 or 0.50. That small piece looks like it could be 5/100 of the circle.)
Ask students to compare the fractions in Question 12. These fractions are close together and are more challenging to compare using the relationship between the denominator and numerator. Encourage students to choose equivalent fractions and the same denominator to compare the fractions.
As students are working, circulate and identify a student or two who can share the strategy they recorded in Question 12D.
- Who would like to describe [student name]'s strategy?
- I know [student name] used a different strategy. [Student name], please show us your strategy.
- Look at Question 12E. Tell your neighbor what you think John did to write that comparison for the fractions in Question 12B.
- What denominator did John use? (10 or a tenth)
- How did he change 1/2 into 0.5? (1/2 = ?/10 and 2 × 5 = 10 and 1 × 5 = 5. So 1/2 = 5/10, which can be written as 0.5.)
- How did he change 36/60 to 0.6? (36/60 = ?/10 and 60 × 6 = 10 and 36 × 6 = 6. So 36/60 = 6/10 can be written as 0.6.)
- Show six tenths and five tenths with the fraction circle pieces. What color pieces did you use? (Purple; the purple piece is 1/10 of the red circle.)
- What size circle piece would you like to use to model the fractions in Question 12C–D? (a hundredth piece because the denominator is a hundredth of the circle)
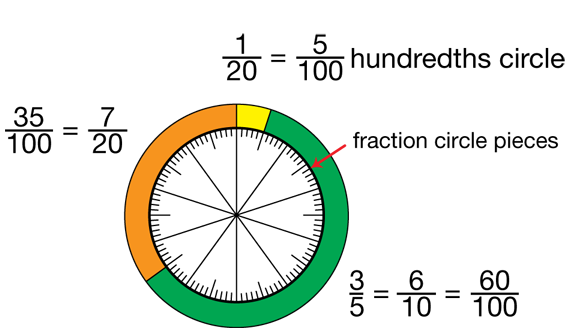
Use the Hundredths Circle. Read the vignette before Question 13 and display the Large Hundredths Circles Master. Direct students to the Small Hundredths Circles page in the Student Activity Book. Students should cut out one of the hundredths circles. Use Questions 13–14 to introduce students to the hundredths circle. This circle adds the hundredths to students' collection of fraction circle pieces. Due to the size of the pieces, students will not cut the hundredths apart. Students will simply lay the fraction circle pieces on the hundredths circle or place the hundredths circle on top of the fraction circle pieces.

The diameter of the hundredths circle is either a little smaller (Small Hundredths Circles page in the Student Activity Book) or little larger (Large Hundredths Circles Master) than the standard fraction circle pieces so students can easily compare them to the hundredth. If your students are using opaque fraction circle pieces you may want to provide copies of the Master so students can easily lay the pieces on the hundredths circle. See Figure 2. Students will use the other circles later in the lesson.
Ask students to use the hundredths circle and fraction circle pieces to discuss and and answer Questions
15–19 with a partner. While students are working, circulate and observe students using the models and reasoning strategies to represent and compare the fractions and decimals.
Hundredths Circle. The area of the hundredths wheel can be defined as one whole. Note that not all fractions translate exactly to decimals using the hundredths circle. For instance, you cannot model 1/3 exactly using the hundredths circle since 1/3 of 100 is not a whole number. However, you can approximate 1/3 using the circle: 33/100 or .33 is close to 1/3.

Make Hundredths Circle Wheels. Ask students to cut out the three remaining circles from the Small Hundredths Circles page in the Student Activity Book. Then show students how to cut along a radius of each circle and fit two circles together to make a wheel. Directions are in the Student Guide. The wheel allows students to show fractions to the hundredths without coloring in the model.
After each student has a hundredths wheel, ask students to work with a partner on Questions 20–21. Each partner should model the fraction with the wheel and then students should compare and check their work.
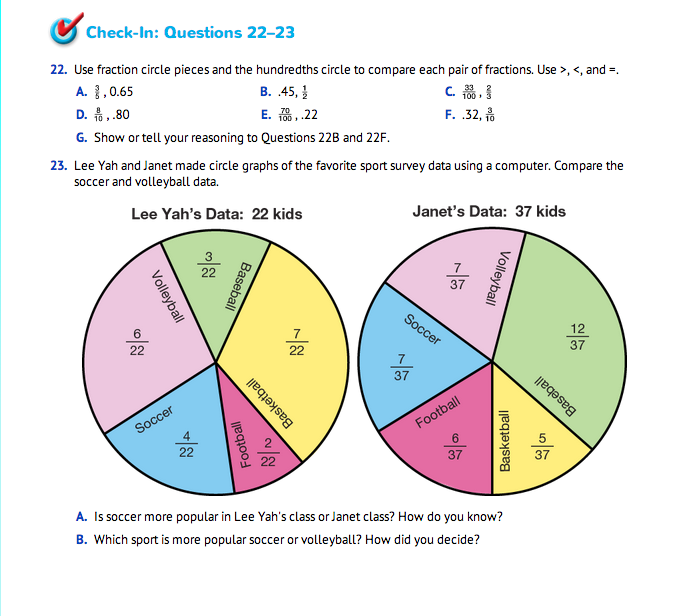
Ask students to complete Questions 22–23 independently.
Use Check-In: Questions 22–23 in the Student Guide to assess students' abilities to use fractions and decimals to represent the same quantity [E1]; make connections among representations of decimals, fractions, area models, and words [E2]; and compare fractions and decimals using models and reasoning strategies [E3].