Display the Good Sports Master. This Master shows the survey data Lee Yah and Janet collected at the start of the lesson in a table and as a circle graph. Discuss the strategies students used to solve the problems in Question 23.
- What strategy did you use to decide if soccer was more popular in Lee Yah's class or Janet's class? (Possible response: I used the hundredth circle. 4/22 is about 0.18 and 7/37 is about 0.19. So 4/22 < 7/37 since 0.18 < 0.19.)
Write the following equations on the board:
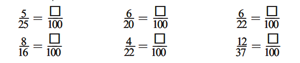
Ask students to show how to solve each problem. See Figure 3 for some possible strategies.
- Which problems did you solve using the hundredths circle? (Possible response: I used the hundredths circle for the problems that had denominators that are factors of 20.)
- Can I show sixteenths on the hundredths circle? (Not easily. I can estimate but the circle is not marked that way.)
- How can I use multiplication and division to change 8/16 to hundredths? (I know 8 × 2 = 16. 50 × 2 = 100.)
- How can you use the hundredths circle to change 6/22 to hundredths? (Possible response: I cannot use it because the circle is not partitioned into 22nds.)
- Can you get an estimate? (Yes. 6/22 is close to 6/20 and 6/20 = 30/100.)
- Who would like to show how to use multiplication and division to solve
 ? (See Figure 3.)
? (See Figure 3.)
- Do you think you can use a similar strategy to change 6/22 to hundredths? (See Figure 3.)
- What is different? (Possible response: When I divide the denominators I do not get a whole number.)
Write the following on the board:
- Is 4 × 5.5 = 22?
- Is 18 × 5.5 = 100?
- What is happening? (Possible response: 100 ÷ 5.5 is not exactly 18; it is 18.181818.)
- Is 4/22 = 18/100? (They are really close to being equivalent.)
- Show how to use multiplication and division to change each fraction on the board to hundredths.
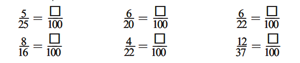
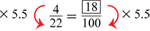












 ? (See Figure 3.)
? (See Figure 3.)