Strategies for Dividing Decimals

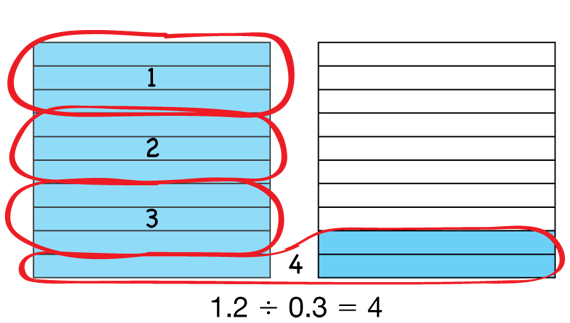
Model and Divide. Use a display of the Tenths Grids Master to demonstrate and discuss how Jason used tenths grids to solve 1.2 × 0.3 in the Model and Divide section in the Student Guide. See Figure 4. Emphasize that the question to ask is “How many groups of 0.3 are in 1.2?” Jason shows 1.2 on the grids and then divides 1.2 into 4 groups of 0.3. In this measurement division problem, you know how many should go into each group, and you have to figure out how many groups there will be.

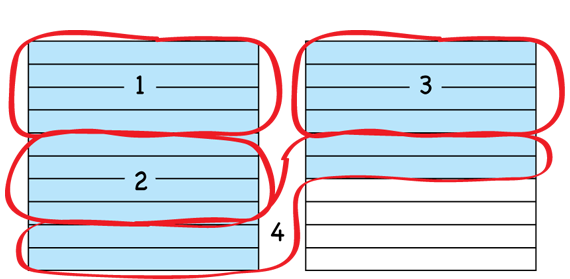
Demonstrate how to use the tenths grid to solve another problem, such as 1.6 ÷ 0.4 on the Tenths Grids display. Find the number of groups of 0.4 that are in 1.6 by circling four-tenth sections of the grids. See Figure 5.

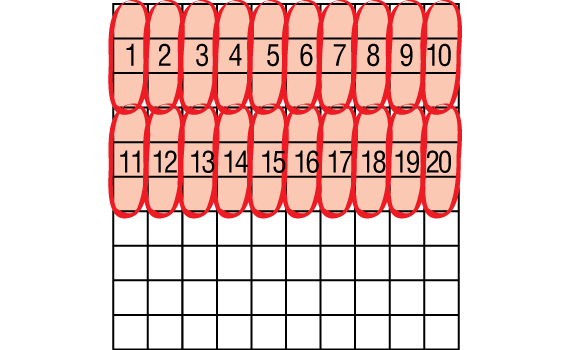
Next ask students how they could use base-ten pieces or the display of the Hundredths Grids Master to solve 0.6 × 0.03. Have student volunteers show how to find the number of groups of 0.03 in 0.6. See Figure 6.

Assign Questions 16–21 to student pairs. Students will use base-ten pieces, grids, and their understanding of place value to divide numbers by decimals less than 1.

Upon completion, discuss students' responses to Question 21. Students should understand that multiplying both the dividend and divisor by a ten to make them whole numbers does not change the quotient. Most likely they will find that when the divisor is in the hundredths, it is easiest to multiply the dividend and divisor by 100; e.g., 21 × 0.07 = (21 × 100) ÷ (0.07 × 100). Likewise, if the divisor is in the tenths such as 21 × 0.7, it is easiest to multiply the dividend and divisor by 10; e.g., 21 × 0.7 = (21 × 10) ÷ (0.7 × 10).

Explore a Variety of Strategies. Display and discuss the vignette that follows Question 21 as a class. The discussion will focus on a variety of solutions to the following word problem presented in the text:

A gardener is planting seeds in rows in his garden. He plants one seed every 4 centimeters, or every 0.04 of a meter. One row is 2.4 meters long. How many seeds will he plant in one row?

To solve 2.4 ÷ 0.04, Chris multiplies both the dividend and the divisor by 100 so he can divide whole numbers. Julia thinks about base-ten pieces and finds 240 hundredths divided by 4 hundredths is 60. Jason uses hundredths grids and Luis thinks about expanded form (200 hundredths × 4 hundredths) ÷ (40 hundredths × 4 hundredths). Assign Question 22 so that students can practice using these strategies to solve division problems.

Use Paper and Pencil. Present the next word problem to the class and ask students to work with a partner to solve it:

A gardener has a bucket of water that holds 21 liters. He wants to fill smaller containers that can each hold 0.6 of a liter of water. How many containers can the gardener fill completely with water?

Discuss students' solution strategies to the word problem. Then display and discuss the vignette that follows Question 23. Discuss the steps Kim takes as she solves 21÷ 0.6 using partial quotients. In order to divide whole numbers, Kim multiplies both the divisor and the dividend by ten in her head, and then moves the decimal point in the divisor and the dividend as she uses paper and pencil to reflect this. To keep the problem the same, when the decimal point in the divisor is moved to make a whole number, the decimal point in the dividend is moved the same number of places.

Assign Questions 24–30 to provide practice using partial quotients and other strategies discussed in the lesson to solve decimal division problems. Have base-ten pieces, and copies of the Tenths Grids and Hundredths Grids Masters available for students to use if desired. The problem in Question 26B result in a remainder. Students can only ignore the decimal points, compute as if all numbers were whole numbers, and place the decimal using estimation.

Review Estimation and Division Strategies. Discuss Check-In: Questions 27–30. Ask student volunteers to demonstrate how they estimate and find the quotients for some of the problems in Question 29. Have displays of the Tenths Grids and Hundredths Grids Masters available.