Review Place Value. To begin this lesson, direct students to the Compare and Order Decimals pages in the Student Guide. In the opening vignette, Mr. Moreno introduces his class to a Digits Game using decimal numbers to the thousandths place. After reading the vignette, have students work with a partner to answer Questions 1–3. After students have had time to discuss their thinking with a partner, ask students to share their solutions. In Question 1, students are asked to find the largest number possible with the digits provided.
After students identify 9765.420 as the largest number, ask:
- Explain how you know that 9765.420 is the largest number that can be made with these digits? (Possible response: You need to put the largest digit in the place furthest to the left because this represents the largest place value. In this number the largest place value is thousands so the digit 9 is equal to 9000. Then the next largest number goes in the place to the right because that is the next largest place value, so the digit 7 is 700. You continue to place the numbers in order from largest to smallest as you move each place to the right.)
- What happens to the value of a digit as you move from left to right? (Possible response: Each time you move one place to the right, the value of the digit is ten time less than or 1/10 of the value of the place directly to the left.)
- What happens to the value of a digit as you move from right to left? (Possible response: Each time you move one place to the left the value of the digit is ten time more than the value of the place directly to the right.)
- What strategy will you use to make the smallest possible number with these same digits? (Possible response: You need to make sure to put the smallest digit in the place furthest to the left and then as you move each place to the right you put the next largest digit each time.)
- What is the smallest number you can make that does not have zero as the first digit? (2045.679)
- What is the smallest number you can make if you can use zero as the first digit? (0245.679)
- How does understanding place value help you decide if you have the largest or the smallest possible number? (Possible response: Using place value tells you the value of each digit in a number.)
- What is 9765.420 in expanded form? (9000 + 700 + 60 + 5 + .4 + .02) How does writing a number in expanded form help you understand the place value for each digit? (Possible response: When you write a number in expanded form you break the number apart to show the value of each digit and then add all the numbers together.)
To provide additional practice with place value, ask students to play several rounds of the Digits Game with a partner using one set of Digit Cards 0–9. It can also be played as a class using the display set of cards. Students can sketch a game board similar to the one in the Student Guide. Vary the game by directing students to find the largest possible number or the smallest possible number.
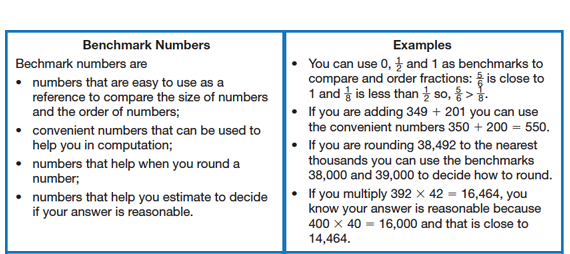
Use Benchmarks. Students are familiar with using benchmarks to compare and order numbers and for rounding numbers. To begin this part of the lesson, ask students to work with a small group to brainstorm what they know about benchmark numbers as well as ways they use benchmark numbers. Encourage students to provide examples. Ask each group to share one or two things they discussed about benchmark numbers. Record students' ideas on a display or chart paper. See Figure 1 for some possible student responses.
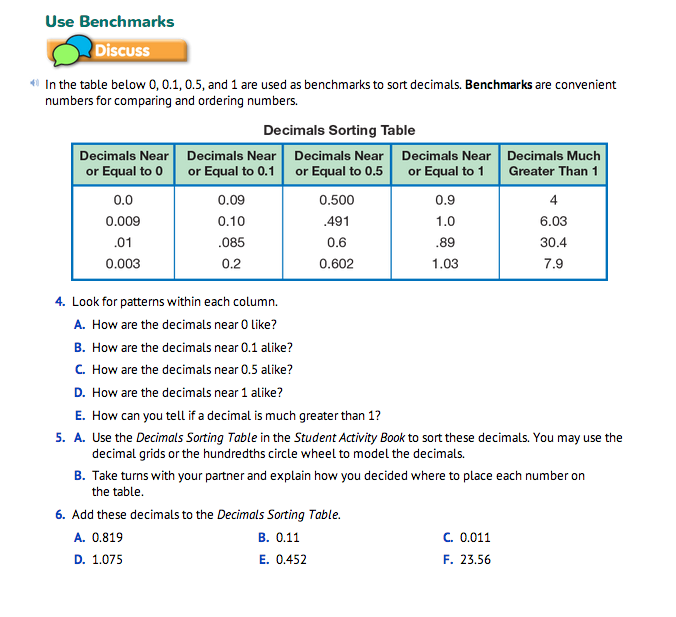
Refer students to the Use Benchmarks section in the Student Guide. Ask students to look at the Decimals Sorting Table at the top of the page, ask:
- What benchmarks are you going to use to think about the size of decimals? (0, 0.1, 0.5, 1, and greater than 1)
- What are the common fraction names for 0.1 and 0.5? ( 1/10 and 1/2 )
In Question 4, students study the numbers under each benchmark in the table and to think about the patterns they see.
- What do you notice about all of the numbers that are close to zero? (They all have zero in the tenths place and either a zero or a 1 in the hundredths place.)
- What patterns do you notice in the numbers that are near or equal to 0.1? (These numbers all have a zero, one, or two in the tenths place. If there is a zero in the tenths place the number in the hundredths place is a high number like 8 or 9.)
- How are the numbers that are near or equal to 0.5 similar? (All of these numbers have a digit that is a five or close to 5 in the tenths place.)
- What do you notice about the numbers that are near or equal to 1? (The numbers either have a 1 in the ones place or they have a high number, like 8 or 9, in the tenths place.)
- What do you see when you look at the numbers that are in last column? (These numbers all have a whole number that is greater than one.)
- Where will the number forty-five thousandths (0.045) go in this table? (in the “near or equal to zero” column) Why do you think so? (0.045 is closer to 0 than it would be to 0.1)

Common Misconceptions When Comparing and Ordering Decimals. John Van De Walle has identified 6 common misconceptions of students when comparing and ordering decimals.
- Longer is larger. Students incorrectly apply whole-number ideas by looking at a number beyond the decimal point as they would a whole number. Under this misconception, students would say 0.534 is larger than 0.9.
- Shorter is larger. Since the numbers to the right of a decimal represent very small quantities, students may think that .4 is larger than .94 since tenths are larger than hundredths.
- Internal zero. Students sometimes confuse the value of the zero in the tenths place. They may think that 0.38 is smaller than 0.085 because they think the zero in the tenths place has no value.
- Less than zero. Students incorrectly think that 0 is larger than 0.36 since the zero in the ones place is a whole number and whole numbers are larger than decimals.
- Reciprocal thinking. Student may incorrectly identify 0.2 as larger than 0.5 because they use their knowledge that decimals are like fractions and connect 0.2 to 1/2 and 0.5 to 1/5 and incorrectly identify 0.2 as larger than 0.5.
- Equality. Students may not understand that 2 tenths is equal to 20 hundredths or 200 thousandths. Students may not understand that 0.2 is close to 0.180 or they may think that 0.6 is smaller than 0.600.
Observing students as they work and understanding these possible misconceptions will help you plan activities to help them overcome these misconceptions.
Students use the Decimals Sorting Table in the Student Activity Book to complete Questions 5–6 in the Student Guide. To complete these questions, students use benchmark to sort decimal numbers on the table. As students work, ask them to share their sorting strategies. Encourage them to use and extend their understanding of place value when discussing their answers.
Use these or similar prompts to encourage discussion:
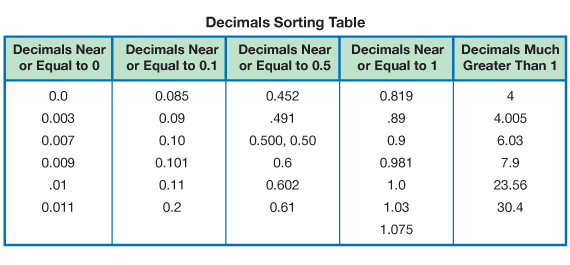
- How did you decide where to place .61 on the chart? (Possible response. I know that 61 hundredths is close to 50 hundredths or one-half.)
- Is 0.61 larger or smaller than 0.5? (It is larger.) How do you know? (0.5 is equal to 0.50. 50 hundredths is smaller than 61 hundredths.)
- Which benchmark number did you use to decide where to place 0.101? (Possible response: I use 0.1 because 0.101 is just a little bit bigger than 0.1.)
- Which benchmark did you use to decide where to place 0.11 on the chart? (0.1) Why? (Possible response: 0.11 is the same as 11 hundredths and 0.1 is the same as 10 hundredths. Eleven hundredths is very close to ten hundredths.)
- Which benchmark did you use to decide where to place 0.011? (0) Why? (Eleven thousandths is a very small number so it is close to 0.)
After students have placed all the numbers in the Decimals Sorting Table, ask each pair of students to take the numbers in one of the columns and put them in order from smallest to largest. Encourage students to use Decimal Grids Masters to help them decide how to order the numbers. See Figure 2.
As students share their work, list the numbers on a display.
Use these or similar discussion prompts and displays of the Decimal Grids Master to encourage students to explain how they decided the order of the numbers.
- How do you know that .01 is larger than .009? (Possible response: I know that one hundredth is the same as ten thousandths. Ten thousandths is greater than nine thousandths so, one hundredth is also greater than nine thousandths.)
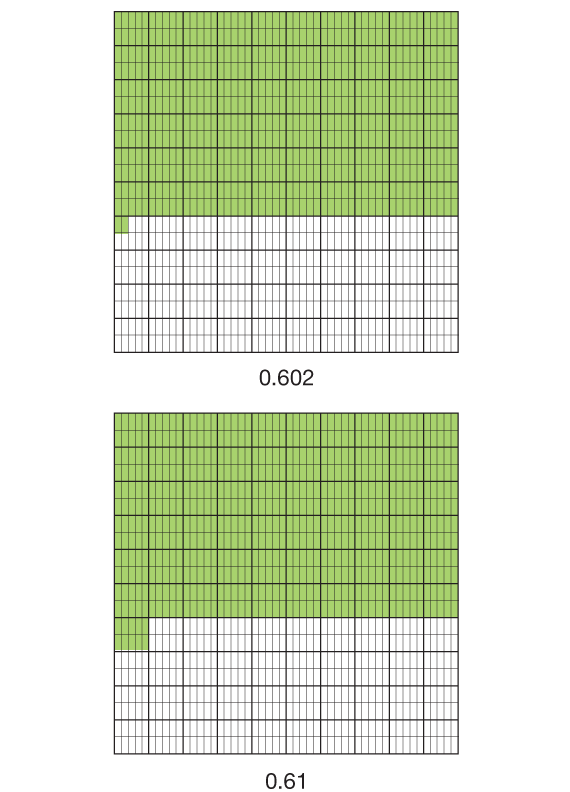
- How can you use the thousandths grid to show that 0.602 is less than 0.61. (Possible response: To show 0.602 I shaded six full rows and two of the little rectangles in the next row. To show 0.61 I had to shade six full rows and one whole square in the next row. Since I shaded less on the grid showing 0.602, that means 0.602 is less than 0.61.) [See Figure 3.]
After students have had the opportunity to share their work, direct them to complete Questions 7–9.