Strategies for Multiplying Decimals

Est. Class Sessions: 3

Developing the Lesson

Part 2. Multiplying a Decimal by a Decimal

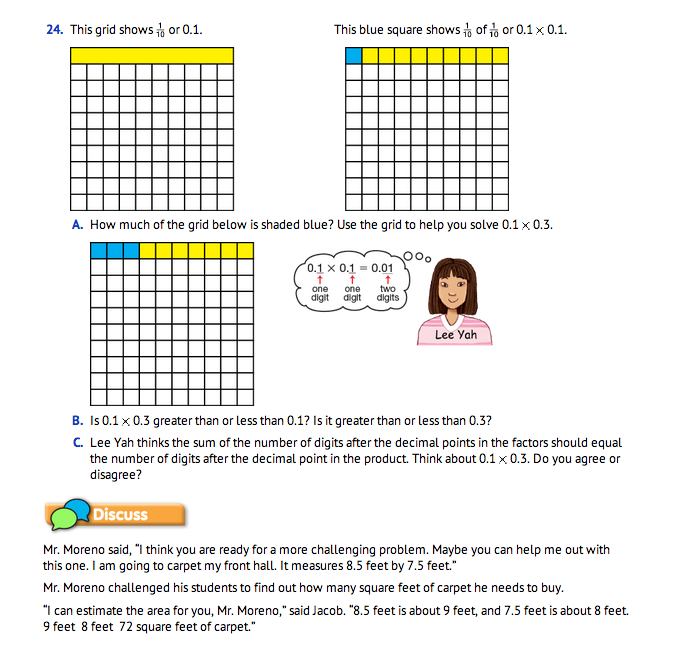
Multiply and Look for Patterns. Assign Questions 19–24. Students begin Part 2 of the lesson by using a calculator to multiply decimals and looking for patterns. These patterns will enable them to place the decimal points appropriately within a product. Encourage students to continue estimating the best they can but to understand that placing the decimal point in a product by estimation is more difficult as the product gets smaller. Students may begin to see that the sum of the number of digits after the decimal points in the factors should equal the number of digits after the decimal point in the product. They will have two strategies to use to place decimal points within products. Students can ignore the decimal points, do the computation as if all numbers were whole numbers, and then place the decimal by estimation or by the rule as described above.

Upon completion, ask students to talk with a partner about Questions 23 and 24C and whether they agree with Lee Yah's observation about placing a decimal point within a product. Some students may agree with the rule, but others may need more convincing. Estimating the product of two decimal factors may help the students who are not yet ready to believe Lee Yah's rule begin to trust that the number of digits after the product's decimal point is equal to the sum of the number of digits after the decimal points in the factors.

After student pairs have had some time to share their thoughts, ask:

How is the number of decimal places in the product of two decimal numbers related to the number of decimal places in each of the factors? (The number of places to the right of the decimal in the product is the same as the sum of the places to the right of the decimal in each factor.)
Can you give an example? Does this rule apply? (Possible response: If I multiply 3 × 0.06 × 0.18, there are two places to the right of the decimal point in 0.18, so the rule applies.)
Estimate the product in the example. Does the placement of the decimal in the answer make sense? (yes)
Why do you think this is so? (Possible response: If I just think about the whole numbers, 3 × 6 is 18. But it is not 3 × 6, it is 3 × 0.06. 0.06 is 100 times smaller than 6, so the product has to be 100 times smaller than 18, too. 0.18 is one-hundredth as big as 18.)

Use Paper and Pencil to Multiply. Read and discuss the vignette concerning Mr. Moreno's carpet order. His students estimate how much carpet he needs for his front hall, which measures 8.5 feet by 7.5 feet. Discuss the convenient numbers the students use to make their estimates. Jacob rounds up to 9 feet and 8 feet. Since both 9 feet and 8 feet are larger than the actual dimensions of the hall, Jacob's estimate is too high. Jackie's convenient numbers are less than the actual dimensions of the room, so her estimate is too low. Jerome's estimate is probably the closest, since one of his convenient numbers is lower and the other is higher than the actual dimensions.

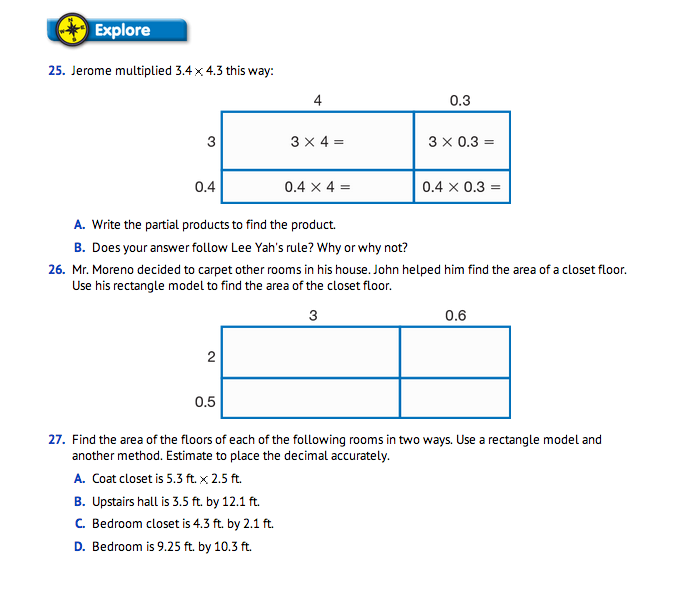
To find the actual amount of carpet needed, the students use a rectangle model and other paper-and-pencil methods to find the exact answer. Discuss the students' use of expanded form and the compact methods, as well as Jessie's example that multiplies 2.6 × 5.1 using all-partials. Explain that students can multiply the numbers as whole numbers first, keeping place value in mind, but ignoring the decimals. Then students can estimate where the decimal point will go and insert it. Students can also apply Lee Yah's rule when placing the decimal point and double check the placement using estimation. See Figure 3 for two examples. In one solution, a student considers the decimals as they work through the problem. In the other, a student simply thinks of whole numbers and places the decimal by estimation.

Assign Questions 25–31. Students may use a variety of strategies to solve the multiplication problems. Upon completion of the problems, ask several student volunteers to demonstrate using a rectangle model, the compact method, all-partials, and expanded form to solve some of the multiplication problems in Question 31. See Figure 4 for examples. Discuss which strategies they used to help them place the decimal points within the products and how they know their answers are reasonable.

Use Check-In: Question 31 on the Strategies for Multiplying Decimals pages in the Student Guide to assess students' abilities to multiply decimals using models and strategies [E8]; estimate decimal products [E9]; and find a strategy [MPE2].

For targeted practice, students can play the Three in a Row game presented in Part 3 of the lesson.