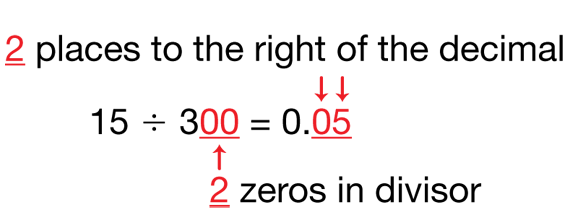Use Invented Strategies to Divide. Students explore division of decimals in a manner parallel to the way they explored multiplication of decimals. Division by decimals is similar to division of whole numbers. In fact, just as with multiplication, division decimal problems can be computed with the same methods used for computing quotients of whole numbers, with the additional task of placing the decimal point in the quotient. Just as with multiplication, students can ignore the decimal points, compute as if all numbers were whole numbers, and place the decimal using estimation. Students will often think about multiplication as they solve division problems because of the inverse relationship between multiplication and division.
The focus in this lesson is using place value patterns and strategies to divide. Begin the lesson by allowing students to find invented strategies with which to divide a whole number by a decimal.
Direct students to the Strategies for Dividing Decimals pages in the Student Guide and the word problem on the page:
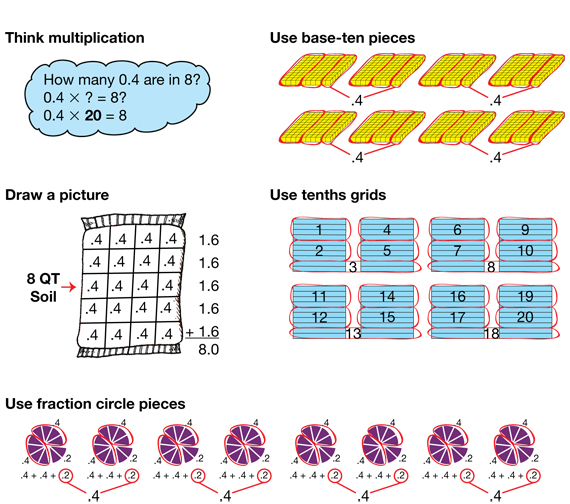
- A gardener wants to plant seeds in small pots. He has an 8-quart bag of potting soil. He needs to fill each pot with 0.4 of a quart of soil.
- Estimate the number of pots the gardener can fill with 0.4-quart of potting soil. Can the gardener fill more or less than 8 pots with soil? Why do you think so? (Possible response: The answer has to be more than 8 because each pot holds less than a quart. 0.4 is close to one-half quart, so for every quart of soil, 2 pots could be filled. I estimate 16 pots.)
- Work with a partner to find the exact number of pots the gardener can fill with soil (Question 1).
Encourage students to use invented strategies to find the exact answer to 8 ÷ 0.4. They can use tools such as base-ten pieces and fraction circle pieces. Students will need to combine their fraction circle pieces or base-ten pieces, or use sketches of the tools in order to have enough to represent 8. Provide access to copies of the Tenths Grids and Hundredths Grids Masters.
Review the terms dividend, quotient, and divisor before discussing students' solution strategies to the problem. See Figure 1. Figure 2 shows some possible strategies for solving 8 ÷ 0.4.
Divide by Tens. Assign Questions 2–6 to student pairs. Students use estimation and patterns to solve the problems. Encourage students to use calculators to help them solve or check the problems so that they can clearly see the patterns that develop.
Discuss the patterns students see when dividing a number by a ten. Compare these observations to those students noticed when multiplying by tens. Write any problems you discuss on the board so that students can clearly see how the decimal points move in division problems. Discuss students' responses to Question 6.
- What does moving the decimal one place to the right show? (It shows that the number is ten times larger.)
- What does moving the decimal one place to the left show? (It shows that the number is ten times smaller.)
- What happens when you divide a whole number by a ten? (It gets 10 times smaller each time you divide it by a ten.)
- How does the decimal point move when you divide a number by a ten? (The decimal point moves one place to the left each time you divide by ten.)
- Who would like to explain a rule for dividing whole numbers by tens? Include an example. (Possible response: It is kind of like when you multiply by a ten, but backwards. Look at the fact in the problem. Then make sure the number of places to the right of the decimal in the quotient is same as the number of zeros in the divisor. For example, 15 ÷ 300 = 0.05. 300 has 2 zeros. I think of the fact 15 ÷ 3 = 5, and then move the decimal point after 5 two places to the left to match the 2 zeros in the divisor.) [See Figure 3.]
- How is this different from when you multiplied a number by a ten? (It is the opposite. The number gets larger. When you multiply by a ten, you move the decimal point one place to the right each time you multiply by ten.)
- How can you use multiplication to check the quotients? Include an example. (Since dividing is the opposite of multiplying, if you multiply the quotient by the divisor, it should equal the dividend. For example, to check 15 × 300 = 0.05, 0.05 × 300 = 15.)
Divide by Decimals Less Than 1. Assign Questions 7–15 to student pairs. Students will use place value understanding and patterns to begin to divide numbers by decimals less than one. They will notice that the resulting quotient is larger than the dividend. This is different from when they divided numbers by tens.
Display 2 base-ten flats, and use a display of the Decimal Grids Master to compare tenths, hundredths, and thousandths grids as you discuss student responses to Questions 8–9.
- How many tenths are in one whole? Two wholes? 10 wholes (Question 8)? (10 tenths, 20 tenths, 100 tenths)
- How much does each small square on the flat show? (one hundredth)
- How many hundredths are in one whole? Two wholes (Question 9)? (100 hundredths;
200 hundredths)
- How many thousandths are in two wholes? (2000 thousandths)
- Explain how to estimate 2 ÷ 0.001. Is the quotient going to be larger or smaller than 2? How do you know? (Much larger because you are trying to find out how many groups of tiny 0.001 are in 2. There will be a lot.)
- Explain how to solve 2 ÷ 0.001. (Possible response: Since I know there are 2000 thousandths in 2 flats, I can think 2000 thousandths divided by 1 thousandth, which is 2000.)
- What happens to the quotient when you divide by 0.1, then 0.01, and then 0.001 (Question 15)? (The quotient gets 10 times larger or the decimal moves one place to the right when you divide by one-tenth. The quotient gets 100 times larger or the decimal moves two places to the right when you divide by one-hundredth. The quotient gets 1000 times larger or the decimal moves three places to the right when you divide by one-thousandth.)
- How is this different from when you divided by 10, 100, and 1000? Why? (When you divide by tens, the quotient gets smaller than the dividend. When you divide by tenths, hundredths, and thousandths, the dividend gets larger.)
- Why does this make sense? (Possible response: When you divide by a ten, the shares are going to be smaller than what you started with. When you divide by small numbers like tenths, hundredths, and thousandths, there will be many small shares.)
Direct students' attention to Questions 10–13 and ask them to describe any patterns they see in the quotients. As you go down the column of problems, each quotient gets 10 times larger. Display the following number sentences and ask students to use patterns and their place value understanding to help you complete them:
72 ÷ 8 = (9)
72 ÷ 0.8 = (90)
72 ÷ 0.08 = (900)
72 ÷ 0.008 = (9000)
- Describe the patterns you see in the divisors and quotients. (Possible response: As you go down the column, the divisors get 10 times smaller and the quotients get 10 times larger.)
- Explain how you used the patterns to solve the problems. (Possible response: I solved the fact, 72 ÷ 8 = 9, then because the divisor was 10 times smaller with each following problem, I knew each quotient would become 10 times larger than the one before it. I just added a zero at the end of the number in the quotient each time.)
- How much smaller is 0.8 than 8? How do you know? (10 times smaller or 0.8 is one-tenth of 8; Possible response: If I multiply 8 × .1, I get 0.8. The decimal point moves one place to the left so I know 0.8 is one-tenth of 8.)
- How much smaller is 0.08 than 8? (100 times smaller, or 0.08 is one-hundredth of 8. Possible response: The decimal point moves 2 places to the left, so that shows that 0.08 is 100 times smaller than 8.)
- How much larger is 0.8 than 0.008? How do you know? (100 times larger; Possible response: 0.008 × 100 = 0.8)
- Can you predict the quotient when you divide a whole number by a decimal less than 1? Will it be more or less than the dividend (Question 14)? (more than the dividend)
- How is this different from when you divide a number by a divisor that is greater than 1? (When the divisor is greater than 1, the quotient will be less than the dividend.)
Assign the Strategies for Dividing Decimals Homework section after Part 1 to provide more practice using estimation and patterns to solve decimal multiplication and division problems.