Assessment in this unit
Key Ideas, Expectations, and Opportunities
Using Assessment to Meet Individual Needs
The explicit expectations and assessment tasks in this unit
describe what it means to "get it." Providing feedback on these
expectations helps identify students who need to access the
content another way, need further practice opportunities, or are
ready to extend or deepen their understanding of a concept.
Instructional opportunities that help support the varied needs of
students also need to be identified. These opportunities provide
models that can be replicated or used multiple times, and can be
used in a variety of settings (e.g., home, transitions, support
classroom, as a center).
The Assessment Program serves the
following purposes:
- It provides information to teachers about what students
know and can do. This information is used to guide instruction.
An activity may help teachers answer questions about whole-class
instruction: What do I do next? In the next minute? Next lesson?
Next class? Next unit? Other assessments may help teachers decide
how to support individual students, including those who struggle
with a concept and those who are ready to be challenged.
- It communicates the goals of instruction to parents and
students. What teachers choose to assess communicates to the
class what they value. For example, if teachers want students to
work hard at communicating problem-solving strategies, then it is
important to assess mathematical communication.
- It provides feedback to students and parents about
student progress. This includes teacher evaluation of student
progress as well as students' assessment of their own progress.
Key Mathematical Ideas
The mathematical content in Math Trailblazers is organized
around a set of Key Ideas. These Key Ideas are based on the National
Council of Teachers of Mathematics (NCTM) Standards for the
grade band as well as current thinking in the mathematics education
community, e.g., Charles (2005), NCTM (2000), Van de Walle (2005).
There is a set of Key Ideas for each content strand: Number, Algebra,
Geometry, Measurement, and Data. They are based on "big ideas" in
mathematics and describe what students should be able to do within
each strand. The Key Ideas are shown in the table in Figure 1.
| 1. Number Sense:
Understand the base-ten number system, recognize relationships
among quantities and numbers, and represent numbers in multiple
ways. |
2. Operations:
Understand the meaning of numerical operations and their
application for solving problems. |
3. Computation and
Estimation: Use efficient and flexible procedures to compute
accurately and make reasonable estimates. |
|
| 1. Identifying Patterns:
Identify and describe patterns and relationships, including how a
change in one variable relates to a change in a second variable. |
2. Tables and Graphs:
Represent patterns and relationships with graphs, tables, and
diagrams. |
3. Symbols:
Represent patterns and relationships with symbols (includes using
variables in formulas and as unknowns in equations). |
4. Using
Patterns: Apply relationships, properties, and patterns to solve
problems, develop generalizations, or make predictions. |
| 1. Shapes: Identify, describe, classify,
and analyze 2- and 3-dimensional shapes based on
their properties. |
2. Orientation and Location: Use
coordinate systems to specify locations and describe spatial
relationships. |
3. Motion: Apply transformations (slides,
flips, and turns) and use symmetry to analyze mathematical
situations. |
4. Geometric Reasoning: Use
visualization, spatial reasoning, and geometric modeling to solve
problems. |
| 1. Measurement Concepts:
Understand measurable attributes of objects or situations (length,
area, mass, volume, size, time) and the units, systems, and
processes of measurement. |
2. Measurement Skills: Use
measurement tools, appropriate techniques, and formulas to
determine measurements. |
| 1. Data Collection: Select, collect, and
organize data to answer questions, solve problems, and make
predictions. |
2. Data Representation: Select and create
appropriate representations, including tables and graphs, for
organizing, displaying, and analyzing data. |
3. Data Description: Describe a data set
by interpreting graphs, identifying patterns, and using
statistical measures, e.g., average and range. |
4. Using Data: Apply relationships and
patterns in data to solve problems, develop generalizations, and
make predictions. |
Figure 1: Key Ideas for Math
Trailblazers (Key Ideas
addressed in Unit 6 are shaded.)
Expectations
To monitor students' growth across and within grades, there are
a set of Expectations that describe what students are
“expected” to do within each content strand. Expectations
show the growth of the mathematical content within the Key Ideas for
each strand.
| EXPECTATIONS |
|
Use this list of expectations to assess students on the
key concepts and skills in this unit. |
| E1* |
Name the partitions of 10. |
| E2 |
Represent addition and subtraction using stories,
drawings, diagrams, counters, number sentences, number lines, or
ten frames. |
| E3 |
Find the related subtraction sentence for an addition
sentence (e.g., fact families). |
| E4 |
Use strategies that apply the properties of addition
(e.g., turn-around, zero) to solve addition and subtraction
problems. |
| E5 |
Find the unknown whole number in an addition or
subtraction equation relating three whole numbers. |
| E6 |
Solve word problems (e.g., join, separate/take away,
part-whole, compare) involving two whole numbers whose sum is less
than or equal to 10. |
| E7 |
Add and subtract within 10 using invented, counting (e.g.,
counting on, counting up, counting back), and reasoning (e.g.,
making ten, using ten, using doubles) strategies. |
| E8* |
Use mental math strategies to add (e.g., direct modeling,
counting strategies, reasoning from known facts) for the facts in
Groups A and B. |
Targeted Practice
This unit provides opportunities for additional targeted
practice for some of the Expectations. See the chart in Figure 3 and
the descriptions that follow. These opportunities connect directly to
assessment tasks, so the practice can be tailored to the current
level of student progress.
- For students who are struggling with the Expectation,
practice is targeted toward the foundational concepts and skills
involved and often provides a different way to access the content.
- For students who are making significant progress toward the
Expectation, practice is designed to help move toward proficiency
and autonomy.
- For students who are already meeting the Expectation,
opportunities are provided to deepen or extend understanding.
| Expectation |
Opportunities for Targeted Practice |
| E1*. |
Name the partitions of 10. |
|
| E2. |
Represent addition and subtraction using stories,
drawings, diagrams, counters, number sentences, number lines, or
ten frames. |
|
| E3. |
Find the related subtraction sentence for an addition
sentence (e.g., fact families). |
|
| E6. |
Solve word problems (e.g., join, separate/take away,
part-whole, compare) involving two whole numbers whose sum is less
than or equal to 10. |
|
| E7. |
Add and subtract within 10 using invented, counting (e.g.,
counting on, counting up, counting back), and reasoning (e.g.,
making ten, using ten, using doubles) strategies. |
|
| E8*. |
Use mental math strategies to add (e.g., direct modeling,
counting strategies, reasoning from known facts) for the facts in
Groups A and B. |
|
* Denotes Benchmark Expectation |
Figure 3: Expectations for Unit 6 with opportunities
for targeted practice
Activities
There is one activity in this unit that can be used to provide
targeted practice. This activity can be placed in a center or used in
another setting or at home.
Games
There are several games in this unit that can be used to
provide targeted practice. Games can be placed in a center or used as
part of class transitions, in another setting, or at home.
Practice Menus
Many of the games and activities for targeted practice are
consolidated in two different Practice Menus. The menus describe
activities that revisit concepts developed earlier in the unit. Based
on students' assessment of their confidence with Expectations E7 or
E8, students select activities from a Practice Menu. The first
practice menu is on the Practicing Addition Facts Homework
Master in Lesson 2. The second is on the Addition Practice
Menu in Lesson 5. See Figure 4. Teacher guidance can help students
find the appropriate level of practice based on evidence from earlier
assessment tasks.
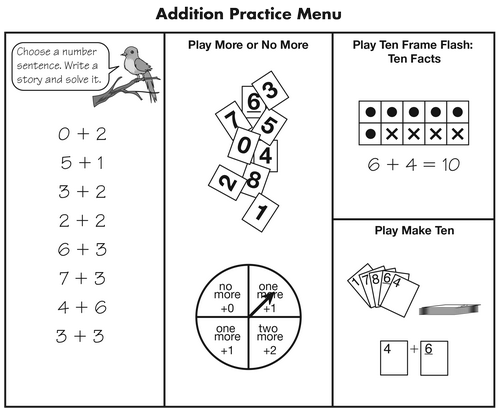
Figure 4: Sample Practice Menu from Lesson 5
) on the Unit 6
Key Assessment Opportunities Chart. See Figure 2. In this unit,
students will also get better acquainted with the Math Practices
Expectations by discussing them in the context of a specific problem
and receiving feedback.