Combining and Partitioning
Est. Class Sessions: 2–3Part 1: Addition Strategies
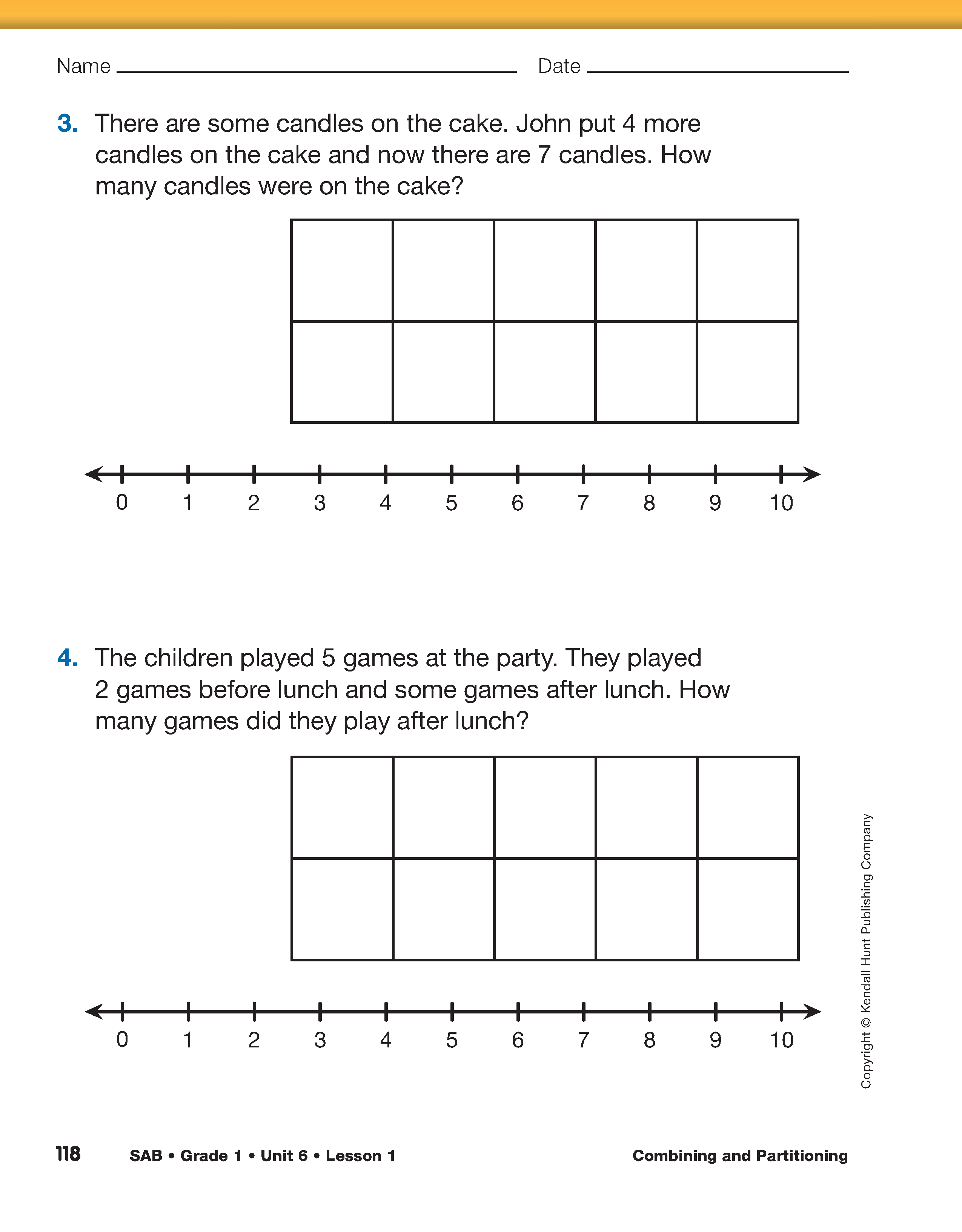
Discuss Addition Strategies. Display the Addition Strategies chart you prepared earlier. Direct students to the Birthday Party pages in the Student Activity Book. Ask students to work with a partner to solve each problem. Provide each pair of students with connecting cubes or counters and encourage them to use the ten frames and number lines on the pages to show how they thought about each problem.
After students have had time to work on several of the problems, use these or similar prompts to guide a discussion about the strategies they used. Encourage students to share as many strategies as they can for each problem.
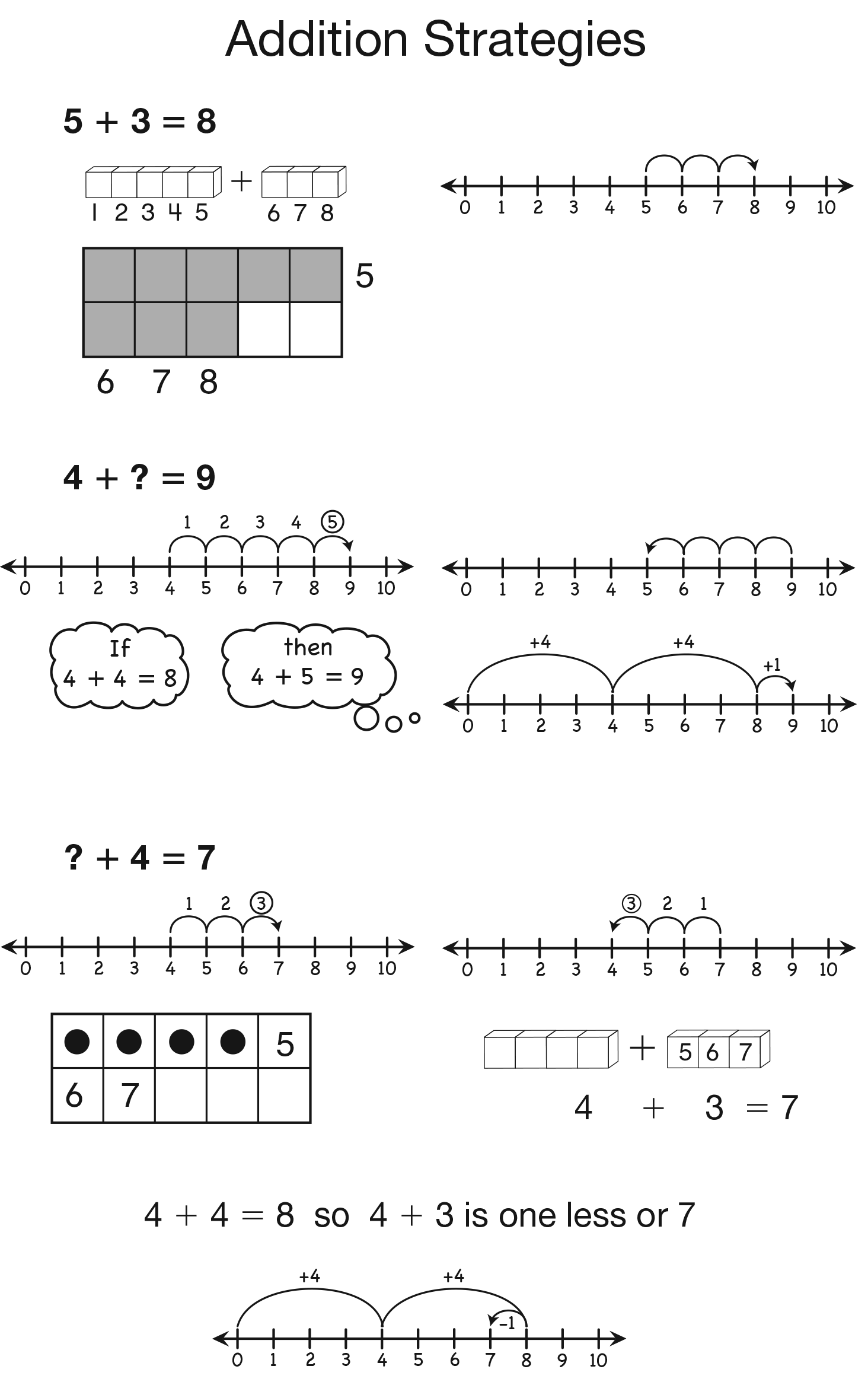
As students share their strategies record them on the Addition Strategies chart adding additional pieces of chart paper, as necessary. See the Sample Dialog.
Continue discussing the solution strategies students used for Questions 1–4, recording student strategies on the Addition Strategies chart. See Figure 2 for a partially completed chart.
Use Sums to Sort Addition Facts to Ten. Show students the addition cards you prepared and tell them they are going to sort the cards by their sums on the Sorting Mats you prepared. Explain that the sum is the answer to an addition problem or the result when two numbers are combined. Use a display of the Sorting Mat to show students how to sort the addition cards as shown in Figure 3. Encourage students to use the tools and strategies listed on the Addition Strategies chart. Ask at least one pair of students to complete the sorting task using large chart paper to create a classroom display.
As students are working, use these or similar discussion prompts to encourage students to explain their thinking.