Lesson 5

Addition Strategies Practice

Est. Class Sessions: 2–3

Before the Lesson

Part 1: Analyze Addition Strategies

Sort Addition Facts by Strategy. Display the Addition Strategies chart created in Lessons 1 and 3. Display the prepared set of Addition Cards for Small Sums 1. Ask students to choose one fact to solve and decide which strategy they like best for this addition fact. As students describe the strategy they have selected, attach the addition fact near the strategy on the Addition Strategies chart.

Ask:

X
  • Which strategy did you use for [2 + 1]? (Possible response: counting on, or one more)
  • Are there other addition facts you would solve using this strategy? (Possible response: 3 + 1; 4 + 2; 2 + 2)

Continue sorting the addition facts displayed until all 12 facts on the Addition Cards are posted near a strategy. If a strategy is not on the chart, add the strategy and then add the appropriate facts. See Figure 1.

All the facts posted thus far involve adding zero, one, or two. To continue to discuss the strategies involved with the other facts, ask students to sort the other Addition Cards you prepared. See Materials Preparation. Give each pair of students at least four cards from the Addition Cards for Small Sums 2 and 3.

Ask students to solve the addition facts they have been assigned and to decide which strategy they like best for each fact. Ask pairs to post their facts near the appropriate addition strategy. Remind students that there is not one right strategy for any given problem and they should post the addition fact near the strategy they used. If a strategy is not present on the Addition Strategies Chart, ask a student to describe the strategy. Add the strategy to the chart, name it, and then add the appropriate facts.

X

Students often associate a strategy with the student who first contributed it or who uses it often. Name that strategy after that student (e.g., Jill's or Bob's). Strategies can also be named by how the strategy works (e.g., counting on). Avoid nonsense names for strategies as they are difficult to remember and refer to.

Look for Patterns in Addition Facts. After all the Addition Cards are posted, ask students to look at the facts and describe any patterns they might notice. Students might notice that all the "zero" facts are grouped together. They may also notice that all the "+ 1" and possibly the "+ 2" facts are grouped together. Students may have also grouped all the facts that make ten or some of the doubles together.

If they have not grouped these together, ask and list their responses:

X
  • What facts have a sum of 10? (1 + 9, 2 + 8, 3 + 7,
    4 + 6, and 5 + 5)
  • Which facts are doubles? (1 + 1, 2 + 2, 3 + 3, 4 + 4, and 5 + 5)
  • How can you use 2 + 2 to solve 2 + 3? (Possible response: 2 + 2 = 4 so 2 + 3 is one more or 5.)
  • How can you use 6 + 4 to solve 6 + 3? (Possible response: 6 + 4 = 10 so 6 + 3 = 9 or one less.)
X

To ensure the strategy discussion is diverse and to differentiate the task, assign a different set of facts to each student pair. Look for students using a variety of tools (e.g., ten frames, number lines, and cubes) to represent their reasoning.

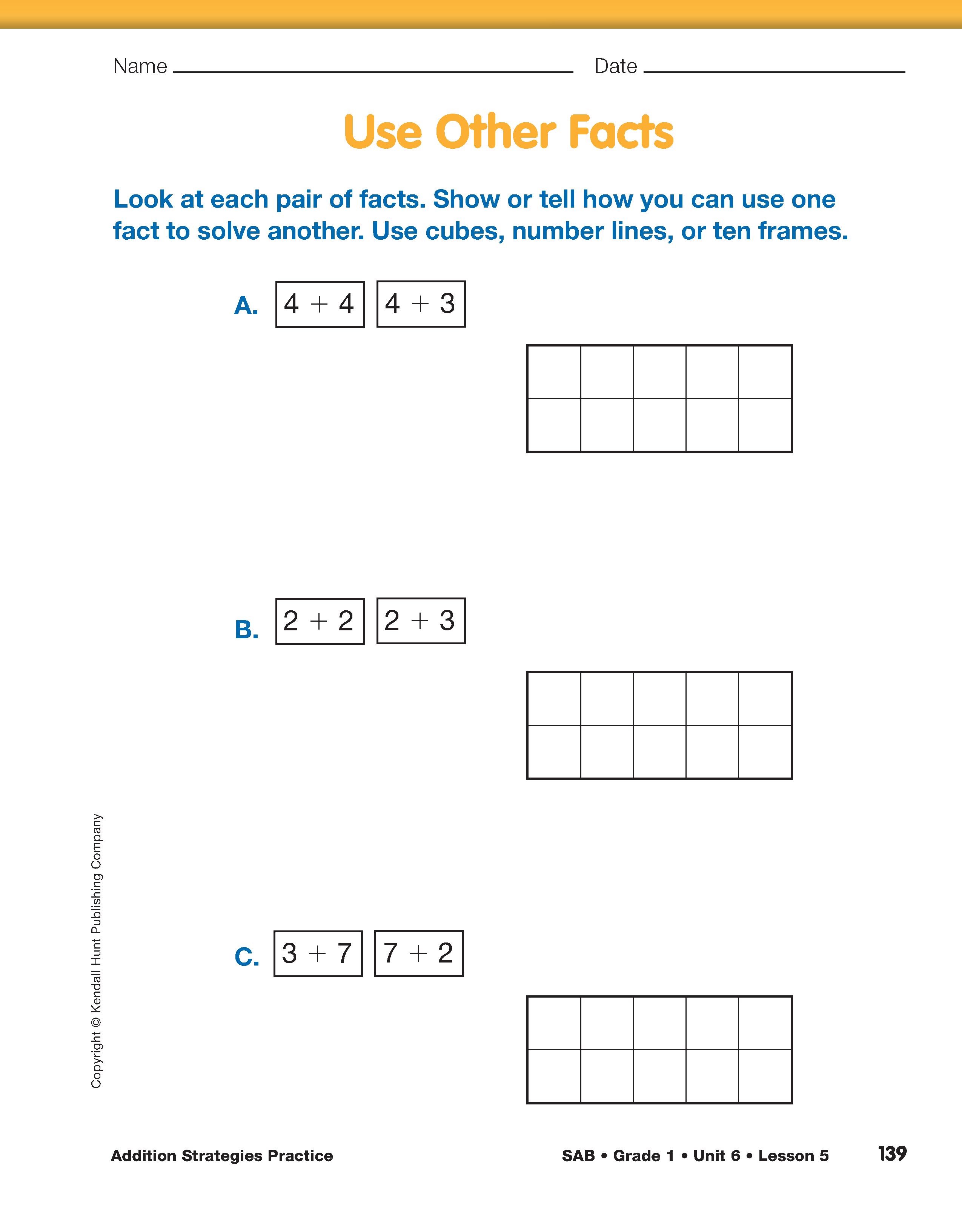
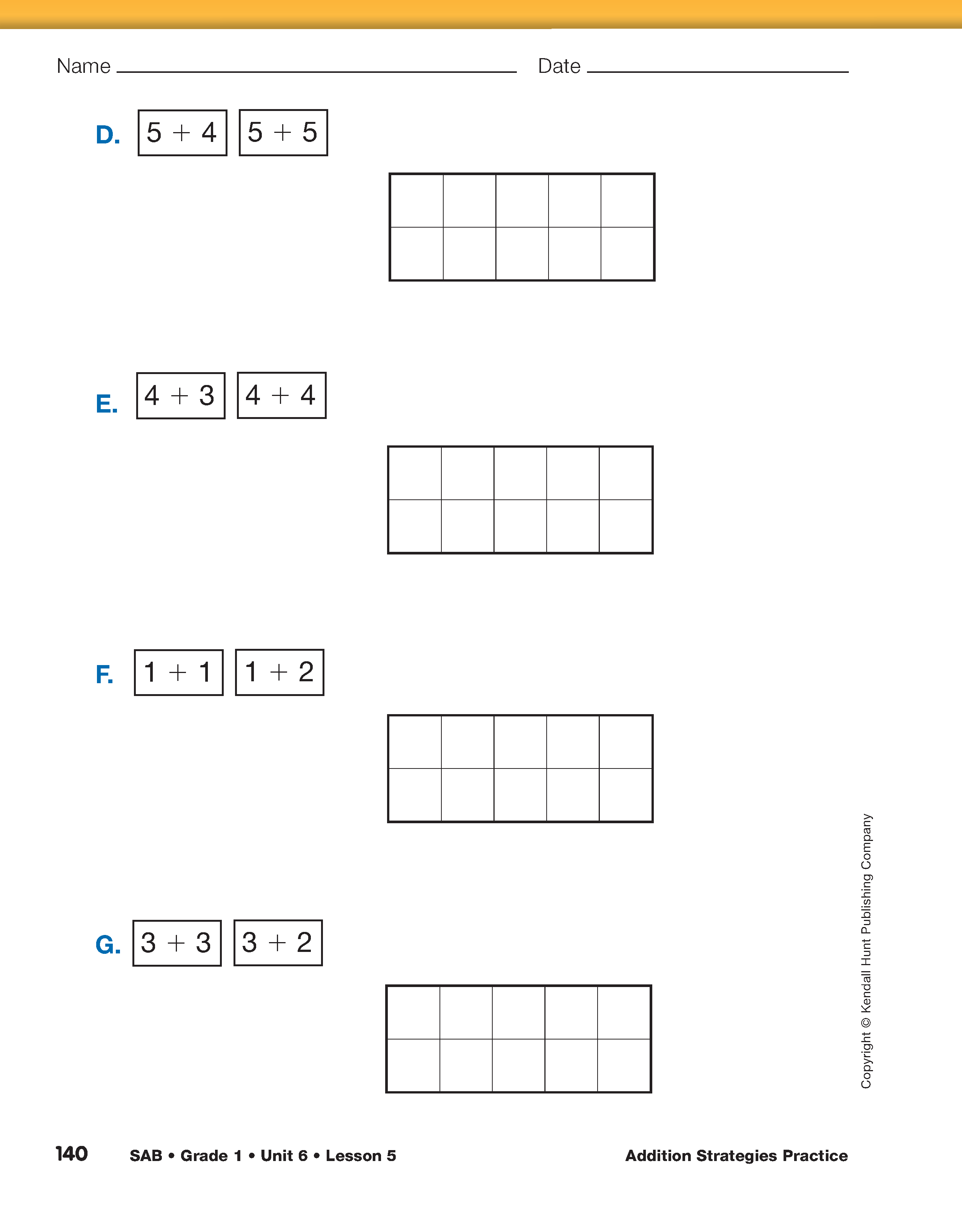
Ask students to continue looking at pairs of facts by assigning the Use Other Facts pages in the Student Activity Book. Students should have 10 connecting cubes, their desk number lines, and ten frames readily available to explain their thinking. Ask each pair of students to be prepared to share their thinking for one pair of facts.

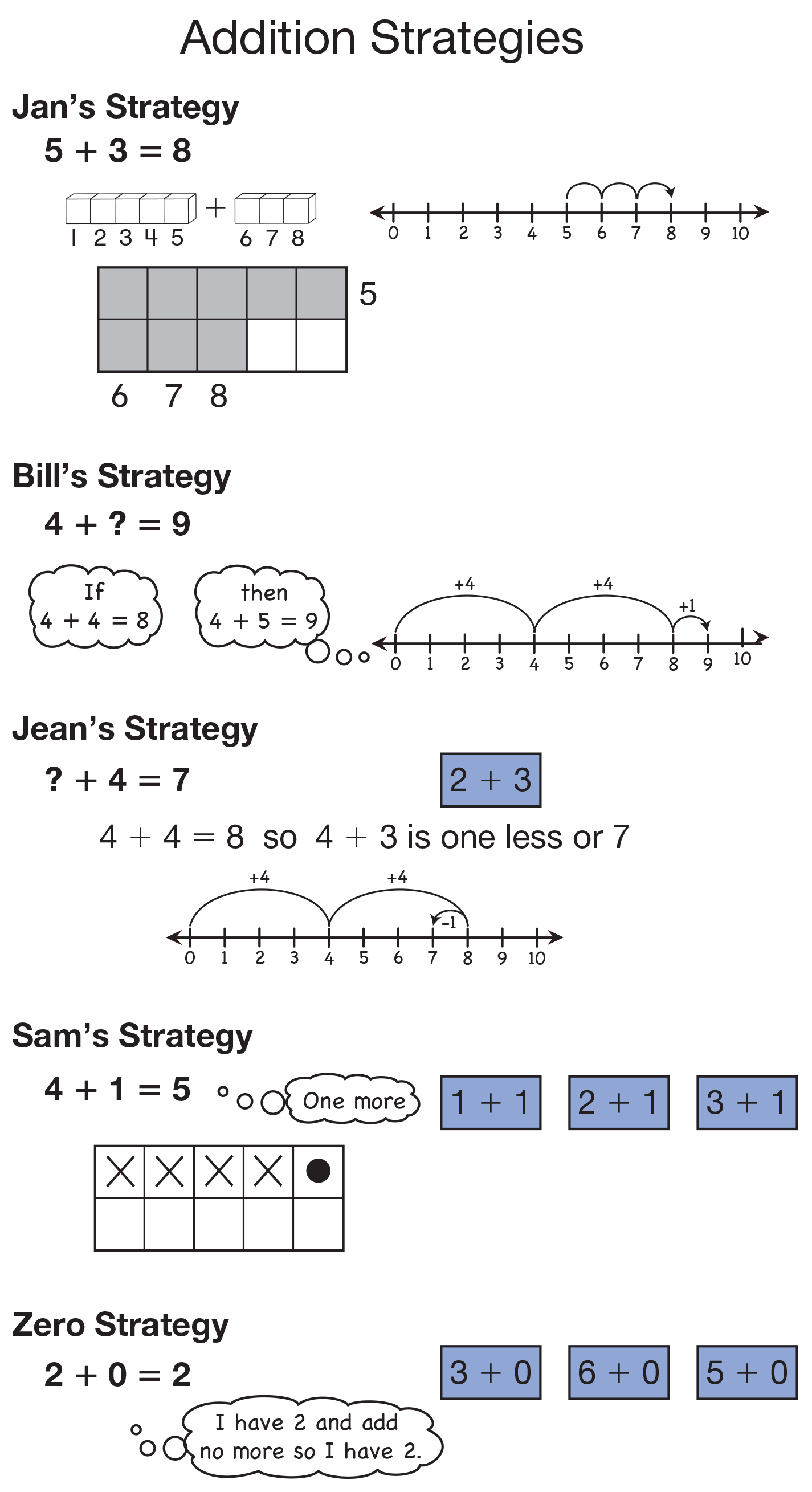
Share Reasoning Strategies. Ask several students to share their reasoning strategies with the class. Look for strategies or tools that may not be represented on the Addition Strategies chart you have displayed. If a strategy or tool is not represented, add it to the chart. Be sure to name it. See Figure 2 for examples of ways to show reasoning or compensation strategies.

Ask:

X
  • Which facts can help you learn other facts? (the partitions of ten, the easy ones like + 1 and + 2, the doubles)
  • Which facts should we work on first then? (Responses will vary: ten facts, doubles, one more or two more)

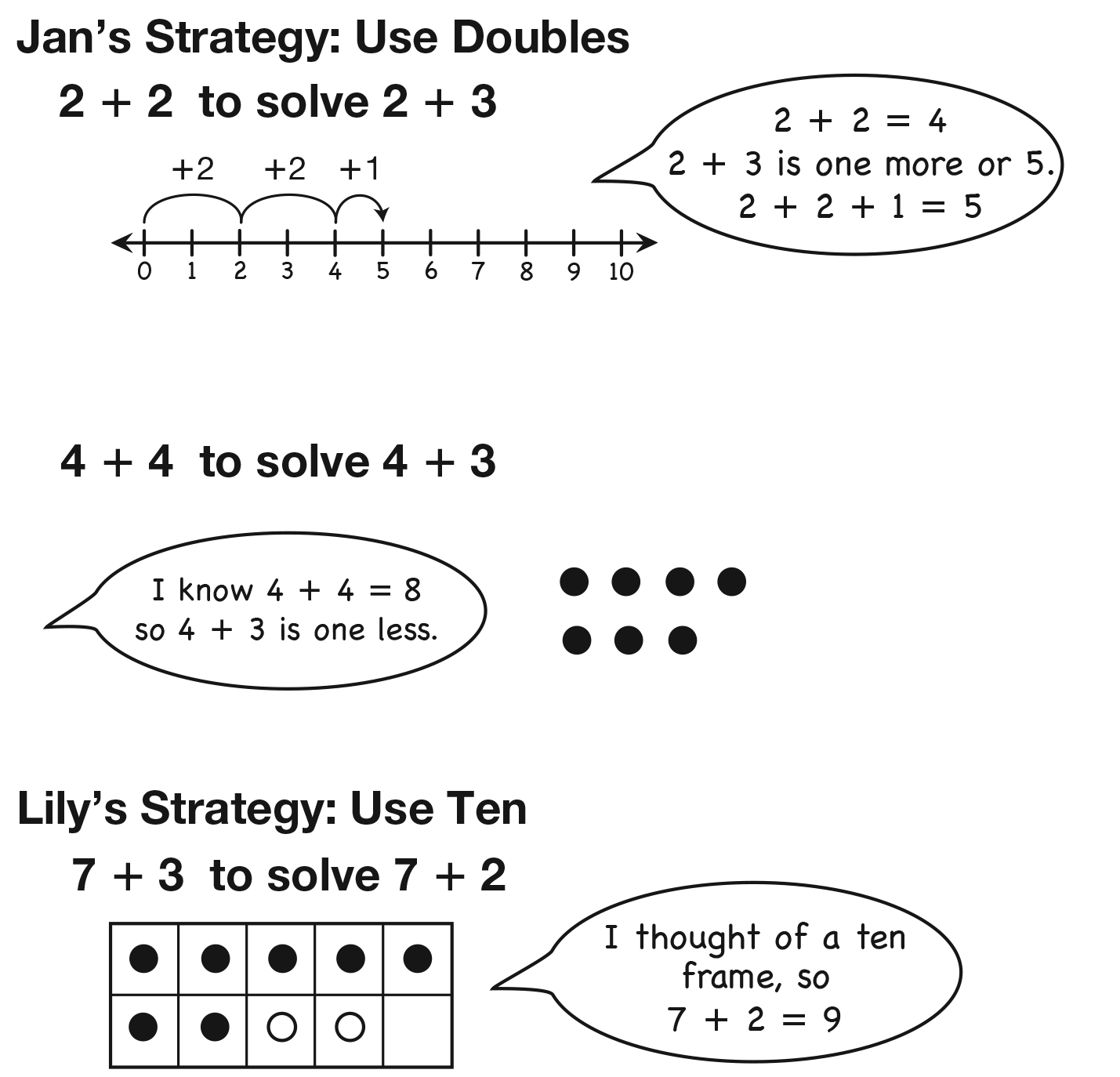
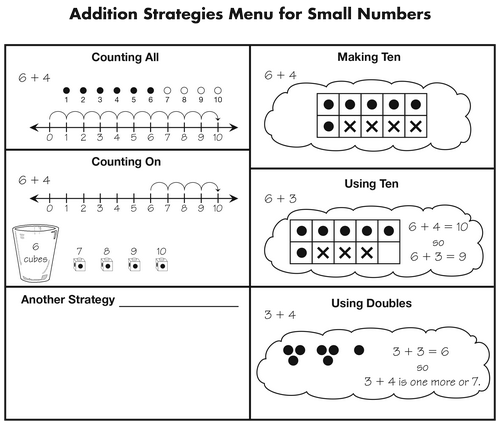
Compare Student Strategies with Strategies Menu. Refer students to and display the Addition Strategies Menu for Small Numbers in the Student Activity Book. See Figure 3. Ask students to look at the menu and compare it to the strategies they have collected on the Addition Strategies chart thus far in the unit.

Ask:

X
  • Which strategies are the same?
  • Add the names from the menu to the names of the strategies on the chart if needed (e.g, add "Using Ten" to "Bob's")
  • Which strategies are on the menu but not on our chart?
  • You showed the counting-on strategy with a [ten frame]. Is that different than showing it with a [number line]? (The strategy is the same, but the tool is different.)
  • Are there any strategies on the Addition Strategies chart that you would like to add to the menu?
X

Reasoning from Known Facts. Using 6 + 4 to solve 6 + 3 is a reasoning or compensation strategy. To acquire operational understanding and fluency with the math facts, students move through three development stages: direct modeling, counting strategies, and reasoning from known facts (Carpenter 1999, National Research Council, 2001).

Direct students' attention to the empty box on the menu and ask students to add their own strategy not represented on the menu. If students need additional room, they can continue to add strategies to the back of the page.

Adventure Book:
Student Activity Book: 139 140
Answers
X
SAB_Mini
+
X
SAB_Mini
+
Master:
Partially completed Addition Strategies chart with facts sorted by strategy
X
+
Ways to show reasoning facts
X
+
Addition Strategies Menu for Small Numbers from the Student Activity Book
X
+