Share Comparison Problem
Strategies. Display the Addition Strategies chart from Lesson 1.
Display the At the Circus page from the Adventure
Book or the Student Activity Book and direct students to
the same page in the Student Activity Book.
- How many clowns do you see? (5)
- How many clowns do you see? (3)
- Are there more clowns or more elephants in the
picture? (more clowns)
- How can you find out how many more clowns there
are than elephants?
Some students may suggest acting out the problem.
Demonstrate this by having five "clowns" line up in a row. Ask
another three "elephants" to come forward and line up in front of
the clowns, two-by-two.
- Are there more clowns or elephants? (clowns)
- How many more? How do you know? (2; Possible
response: When you match up the two rows, there are two clowns
with no elephant in front of them.)
- What tools can you use to solve the problem?
(Possible responses: ten frame, a number line, connecting
cubes, counters)
- How can you use connecting cubes to solve the
problem? (Make a train of 5 cubes for the clowns and a train
of 3 cubes for the elephants. Match up the train of 5 to the
train of 3 and then count the unmatched cubes. There are 2
more cubes on the 5-cube train.)
Part-whole diagrams are models for take away/separate
problems and part-whole/part-unknown problems. A part-whole
diagram does not model the comparison situations presented in
this lesson because there are two wholes. Use ten frames, two
trains of connecting cubes or links, and counters to model
comparative problems.


Comparison Situation. Compare is the third of the
three main subtraction situations described in
Mathematics in this Unit. In this situation, two quantities
are known and the task is to determine how much larger or
smaller one is from the other. (John has 5 cookies. Mary has 2.
How many more cookies does John have than Mary?) This situation
is conceptually different from the two situations already
discussed (take away/separate and part-whole/part-unknown)
because it is not a part-whole model. In the comparison
situation, there is no single whole. Instead, there are two
distinct wholes, which are being compared to determine the
difference in size or quantity. See Mathematics in this Unit
for further discussion.
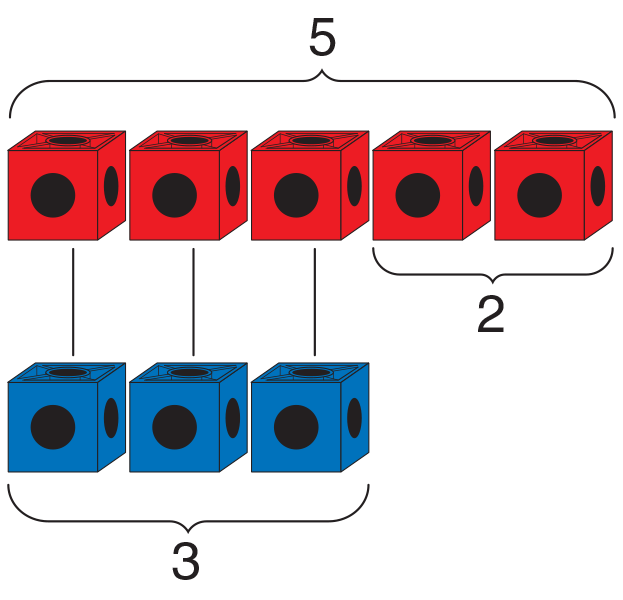
Display a train of five red cubes and a train of three blue
cubes. Ask students to make the two trains. Draw lines to match
up the cubes in the two different rows as in Figure 2.
- How many more blue cubes (elephants) do you
need to equal the number of red cubes (clowns)?
(2 more blue
cubes; 3 of the cubes in each train match up. There are 2
unmatched cubes. If there were 2 more elephants, there would
be 5, the same as the number of clowns.)
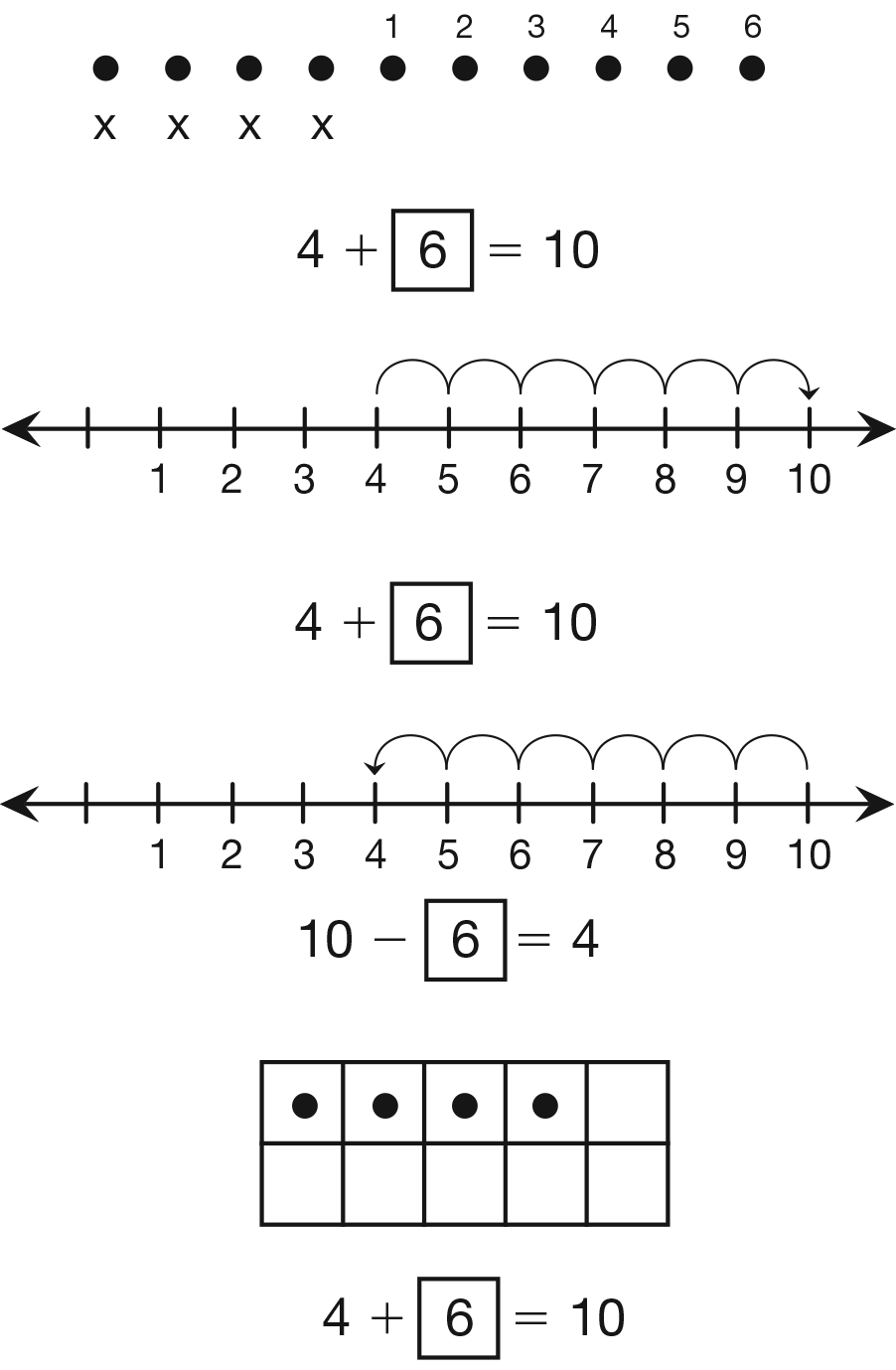
- In the number sentence 3 +
= 5, what does the 3 represent?
(elephants) The 5? (clowns)
- What number is missing? How do you know? (2; I
need to add 2 to the 3 to make 5.)
- Now use your number line to help compare the
number of clowns to the number of elephants. Do you get the
same answer? (Possible response: Yes; I find 3 to show how
many elephants there are. Then I need to move forward on the
number line because there are more clowns than elephants. I
move forward 2 to get to 5, so I know 3 + 2 = 5. There are 2
more clowns than elephants.)
- Is there a strategy on the Addition Strategies
chart that could help? (Possible response: I use a counting-on
strategy. I start at 3 and count on two times to get to 5, so
I know there are 2 more clowns than elephants.)
- Is there another way to solve this problem?
(Possible response: 3 + 3 = 6 so 3 more elephants would make
6, but that's too much. 3 + 2 = 5. 2 more elephants would make
5, the same number of clowns because there are 2 more clowns
than elephants.)
- Should we add this strategy to the Addition
Strategies chart? (List any new strategies on the chart. See
Figure 5 for example strategies.)

In this lesson, addition strategies are used to model and
solve comparison situations. Because they are building on what
they know, students will probably write an addition number
sentence to describe a comparative situation. However, some
students may want to use subtraction strategies and sentences to
solve and describe the problems in this lesson. Accept all
strategies and either addition or subtraction sentences,
provided the sentence accurately fits the problem situation.
Later in the unit, students will make connections between
addition and subtraction and move toward using subtraction to
solve and describe problems.
Generate and Solve Comparison
Problems. Display the How Many More at the Circus chart you
prepared prior to the lesson. See Materials Preparation. There
are other examples on the At the Circus page that can be
compared to find the difference. Invite students to look at the
picture for another comparison situation. See Figure 3 for a list
of possible comparisons.
Have a student volunteer suggest a comparison. For example,
he or she could suggest comparing the number of balloons to the
number of juggling balls.
- Are there more [balloons] or more [juggling
balls] in the picture? (balloons)
- Complete this statement with what we want to
know: How many more _______ than _______? (How many more balloons
than juggling balls?)
Fill in one of the cloze sentences listed on the chart with
the student's suggestion. Refer students to the Addition
Strategies chart from Lesson 1 and ask them to choose a strategy
to solve the problem. Ask a student to share his or her solution
strategy. Have the other students check the answer by modeling
the situation with two trains of connecting cubes.
- What is a number sentence that describes this
situation? (For the example problem, 7 + 3 = 10.)
- What do the numbers represent in this number
sentence? (For the example problem, there are 7 balls and 10
balloons. 3 more items must be added to the 7 to make 10. I
know that means there are 3 more balloons than balls.)
- Is there another way to solve this problem?
(Possible response: To compare 10 balloons to 7 juggling
balls, I thought about making a ten and put 7 Xs in a ten
frame. I needed 3 more to get to 10, so I knew there are 3
more balloons than juggling balls.)
Write the solution in words and record an addition number
sentence with a missing addend as shown on the sample chart in
Figure 4.
Complete another comparison problem as a class and record
the information on the chart. Ask questions similar to those in
the example.
Now ask students to simply generate additional comparison
situations. List them on the chart by filling in the cloze
statements. After many comparison ideas have been listed, have
students work with a partner to choose and solve one of the
problems. Ask students to use the How Many More at the
Circus page in the Student Activity Book to record the
comparison problem of their choice and its solution.
Before students begin their work, display and direct their
attention to the Math Practices page in the
Student Activity Book Reference section. Explain that they will
need to choose good tools and strategies to solve their problem
[MPE2] and that they should refer to the Addition Strategies
chart as needed. Ten frames and number lines are provided on the
page, and connecting cubes should be readily available for
students to use as they wish. Students are asked to solve the
problem a second way. This is one way to check the answer to
their first solution [MPE4]. For both solutions, students are
asked to show their work [MPE5] so that others can understand
their thinking.

Use the How Many More at the Circus pages in the
Student Activity Book with Feedback Box to assess students'
abilities to represent comparative subtraction using stories,
drawings, counters, number sentences, number lines, and ten
frames [E2]; find the unknown whole number in an addition or
subtraction equation relating three whole numbers [E5]; solve
comparative word problems [E6]; add within 10 using invented,
counting, and reasoning strategies [E7]; know the problem
[MPE1]; find a strategy [MPE2]; check calculations [MPE4]; and
show work [MPE5].
Monitor the students as they work so you can select several
to present a variety of solution strategies. Students who finish
early can solve another problem on the list or create one on
their own.