Display the At the Circus page from the Student
Activity Book in Lesson 3 or in the Adventure Book and
the How Many More at the Circus chart from Lesson 3. Ask students
to recall some of the comparison situations they made about the
circus picture.
- Look at the At the Circus page. Compare
the number of clowns to the number of bananas. How many
clowns are there?
(5) How many bananas are there? (8)
- Are there more clowns or bananas? (bananas)
- How many more bananas are there than clowns? (3)
How do you know? (Possible response: A train of 8 cubes
is 3 longer than a train of 5 cubes.)
- Explain how we can solve the problem. (Possible
response: We start at 5 and count up until we get to 8. I
counted up 6, 7, 8—that's 3 more.)
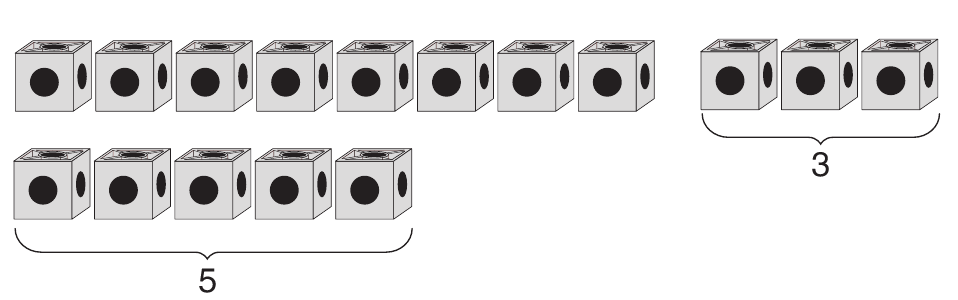
Ask students to make two trains of cubes, using red cubes
for the clowns and yellow for the bananas. Have students line up
the two trains in two different rows on their desks. Demonstrate
by making a train of 8 yellow cubes to represent the bananas and
a train of 5 red cubes to represent the clowns.
Display the two trains, one below the other, and
draw lines to match up the cubes in the two different rows.
- How can you use the cube trains to decide how
many more clowns than bananas? (There are three more yellow
cubes than red cubes. When we match the cubes that represent
the bananas and the cubes that represent the clowns, there are
three yellow cubes left that are not matched with the red
cubes. We can say there are 3 more bananas than clowns.)
- What is a number sentence for this situation?
(Possible responses: 5 +
= 8 or 8 − 5 = 3)
- When we find out how many more, we can write a
subtraction number sentence or an addition number sentence.
We can write 5 +
= 8, but what is the subtraction number sentence for this
situation?
(8 − 5 = 3)

Have students solve the problem by acting it out. Have 8
students line up in a row to represent the bananas and 5
students in another row to represent the clowns. Ask:
- Are there more bananas or clowns? (bananas)
- If we match up the bananas with the clowns, how
many more bananas are there? (3)
Demonstrate other situations with students, such as a row
of 5 students and a row of 3 students. How many more students
are in one row than the other row?
Students may or may not see this as a subtraction situation. Give
them a visual model of taking away the parts that match up,
leaving only the difference. See Figure 1. Show the two trains of
cubes side by side. Break away the parts that match and hold up
the remaining three cubes. You may also use a display of the
Ten Frames page in the Student Activity Book Reference
section to show the difference.
Write 5 +
= 8 and 8 − 5 =
on the board.
- How can both number sentences represent the
problem, how many more bananas are there than clowns? (They
each show a different way to think about how many more bananas
there are than clowns.)
- Tell the story that matches 5 +
= 8.
(Possible response: There are 5 clowns. How many more are
needed to have 8 clowns?)
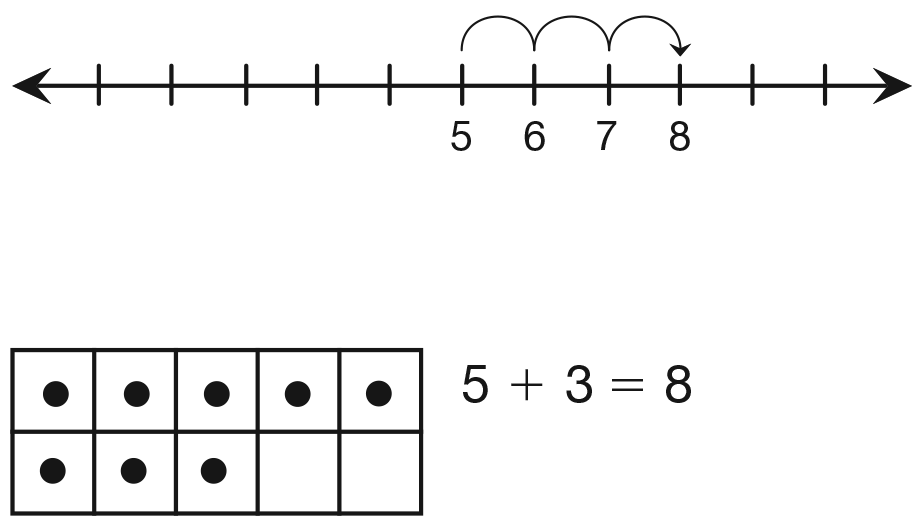
- What strategy did you use to solve 5 +
= 8?
(Possible response: I counted up to 8. I started at 5 and
counted 6, 7, 8. That is three hops.) [See Figure 2.]
- Tell the story that matches 8 − 5 =
.
(Possible response: There are 8 bananas and 5 clowns. How many
bananas are left if each clown takes one?)
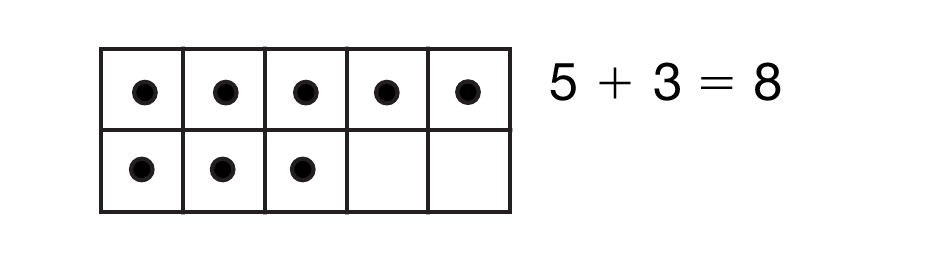
- What strategy did you use to solve 8 − 5 =
?
(Possible response: I thought about the ten frame. I know 8 is
5 + 3. If I hide 5, there are three left.) [See Figure 3.]
Point out that when students use an addition number sentence to
solve a comparison problem, the difference is the missing
addend. Students may solve the addition problem 5 +
= 8 and say that 3 is the missing addend, but then say the
difference is 8 because students often assume that the answer is
always after the equal sign. To emphasize the answer in both the
addition and subtraction number sentences, draw a box around the
number that tells how many more in each number sentence. Remind
students that for an addition number sentence, you can change the
order of the addends and the sum will be the same. For a
subtraction number sentence, write the largest number first.

Students may use various strategies to solve subtraction
problems. The following is an explanation of some of the
strategies:
- Counting Up: Students may use this strategy for
problems with missing addends. For example,
6 +
= 10. Start with the lower number and count up to 10: 7, 8, 9,
10. The answer is 4.
- Counting Back: Students may use this strategy
for subtracting smaller numbers. For example, to solve
10 − 2,
students count back 2 numbers: 9, 8. The answer is 8. Counting
back is similar to the counting-on strategy but the numbers are
getting smaller instead of larger.
- Reasoning from Related Addition and Subtraction
Facts: As students begin to understand fact families, they may
use related addition facts to solve subtraction facts. For
example, knowing 4 + 3 = 7 will help students solve 7 − 4 and 7
− 3.
Invite students to find other comparison situations on the At
the Circus page. Have students select a situation and model it
by making two trains of connecting cubes. Look at the How Many
More at the Circus chart you prepared in Lesson 3 of this unit
for a list of comparisons students can make on the circus page.
See Figure 4 for a sample chart. Use the display of the first How
Many More page from the Student Activity Book to
demonstrate a sample problem including an addition number
sentence and a subtraction number sentence. For example, there
are 7 balls and 10 balloons. How many more balloons than balls?
7 + 3
= 10 and 10 − 7 = 3
Have student pairs write their own compare problems and number
sentences on Question 1 of the How Many
More page in the Student Activity Book .