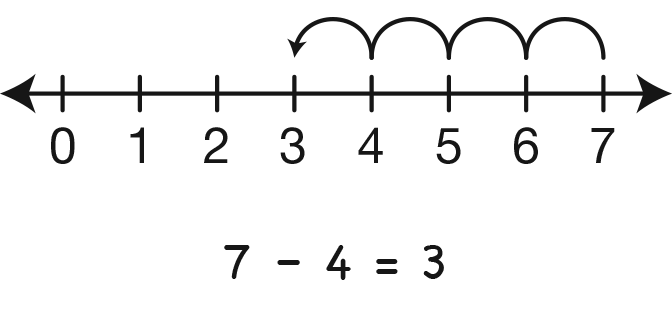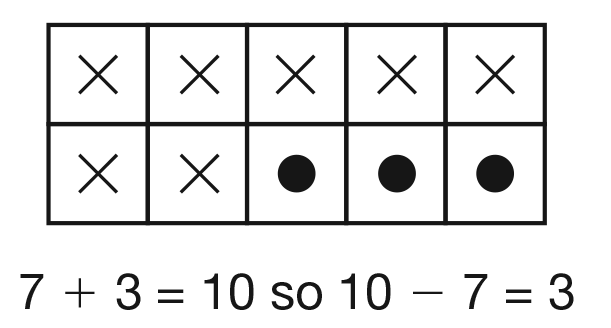Use Addition and Subtraction Strategies.
Pose the following problem:
There were 7 wolf pups in a den at the zoo. The zookeeper
took 4 out of the den. How many were left in the den?
Model the problem using a bag to represent the
wolves' den and connecting cubes to represent the wolves. Ask
students to model the problem with connecting cubes.
- What number sentence describes this problem?
(7 − 4 = 3)
- What do the numbers in the number sentence
represent? (7 wolves; 4 wolves taken away; 3 wolves left)
- Is there another way to solve the problem?
(Possible response: I use a number line. I start at 7 and
count back 4 hops. I land on 3.) [See Figure 3.]
Direct students' attention to the problems on the At the
Zoo pages in the Student Activity Book. Display the
Math Practices page in the Student Activity Book
Reference section. Explain that their work will involve attention
to three Math Practices in particular: [MPE1], Know the problem;
[MPE2], Find a strategy; and [MPE5], Show my work. They can use
connecting cubes or counters, number lines, and ten frames and
any strategy they choose to solve the problems. In
Question 7, they will show or tell how they solved the problem
with words or drawings, MPE5. Remind students to include details
about any tools they used.
Ask students to work in pairs to solve the problems.
Monitor students as they work. Look for examples of students
using tools like number lines, connecting cubes, diagrams or
drawings, and ten frames. Also look for students using counting
strategies like counting on, counting back, or reasoning
strategies like making ten, and thinking addition strategies.
For students who need more of a challenge, ask them to
solve problems a second way, or in as many different ways as
they can. Acknowledge that their answer is correct, but
encourage them to practice using other strategies that may be
useful in the future. For example, "I see that you are able to
use a ten frame really well. Can you show how to use a number
line?" Help students who say, "I just know the answer" practice
articulating their explanations by saying, "Can you show how you
know by using one of our strategies?"
Share Strategies.
Upon completion, ask the students you noted to show
how they used the tools and strategies to solve the problems by
asking the following questions:
- What two things are being compared in Question
1? (The price of an adult ticket is being compared to the
price of a child's ticket.)
- [Student name], show how you used a counting
strategy to solve the problem in Question 1. (Possible
response: I thought 7 plus how many more equals 10? I counted
up 3 from seven. I put 7 in my head and then ... 8, 9, 10. 7 + 3
= 10.)
- [Student name] used a ten frame to solve the
same problem. Did you think about making ten? Can you show us
how? (Possible response: I pictured 7 Xs in the boxes to show
the price of the child ticket. 3 more boxes were needed to
make ten, so that is how much more the adult ticket costs than
the child's.) [See Figure 4.]
- In Question 2, there are some parts and a
whole. What is the whole? (the 6 monkeys total)
- What is one of the parts? (the 4 monkeys on the
floor)
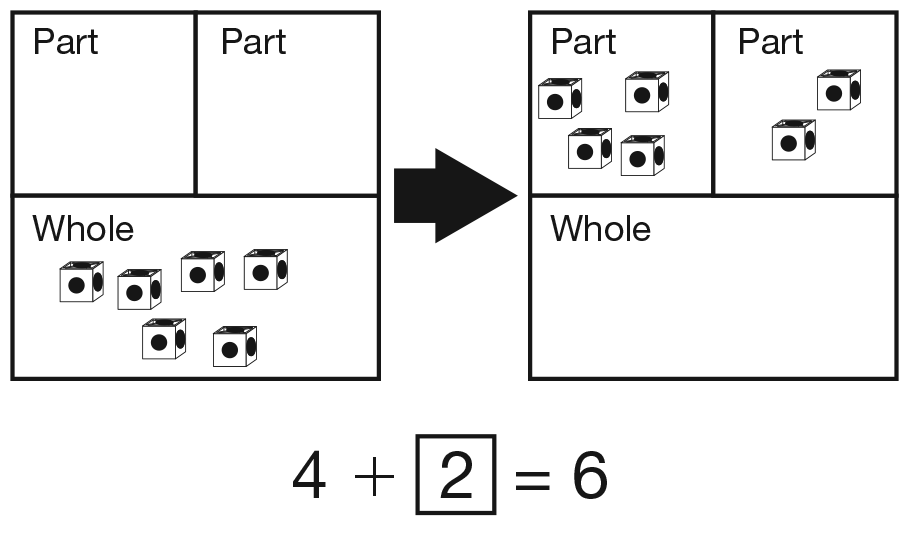
- [Student name], show how you used a
part-whole diagram to find the other part. (Possible
response: I put 6 cubes in the whole section, then I moved 4
to one part section. I moved the remaining cubes to the other
part section and counted them. There were 2.) [See Figure 5.]
- What is a number sentence that describes this
problem?
(4 + 2 = 6 or 6 − 4 = 2)
- What do the numbers represent in the number
sentences? (4 monkeys on the floor plus 2 monkeys in the tree
equal 6 monkeys total. Or 6 monkeys total, take away the 4
monkeys on the floor, and there are 2 monkeys in the tree.)
- Show how to use a number line to solve the
problem in Question 2. (I started at 4 and hopped forward
two times to 6. 4 + 2 = 6. 2 is the missing part so there were
2 monkeys in a tree.)
- Show or tell how you solved the problem in
Question 3. Include a number sentence. (Possible response:
Lin shared zero pieces of candy. I thought about subtracting
0. When I take 0 from a number, the number stays the same, so
3 − 0 = 3.)
- In Question 4, what is being taken away? (2
seals)
- How did you solve this problem? (Possible
response: I took 8 cubes and made a train. Then I took 2 away
because 2 seals were on the rocks.)
- Explain how to count back to solve the problem.
(Start at 8 for all the seals in the water. Count back 7, 6
for the two seals on the rocks. So there are 6 seals left.)
- Question 5 is also a compare problem. How did
you you solve it? (Possible response: I started at 9 and
counted back three times: 9, 8, 7, 6 so 9 − 3 = 6.)
Ask students to find a new partner with whom they can share their
answers to Questions 6–7. After the pairs have
conferred, select a student to demonstrate how to use a ten frame
to help see the difference between the number of tigers in the
Big Cats building (5) and the total number of cats (10). The
difference is the number of lions in the building.

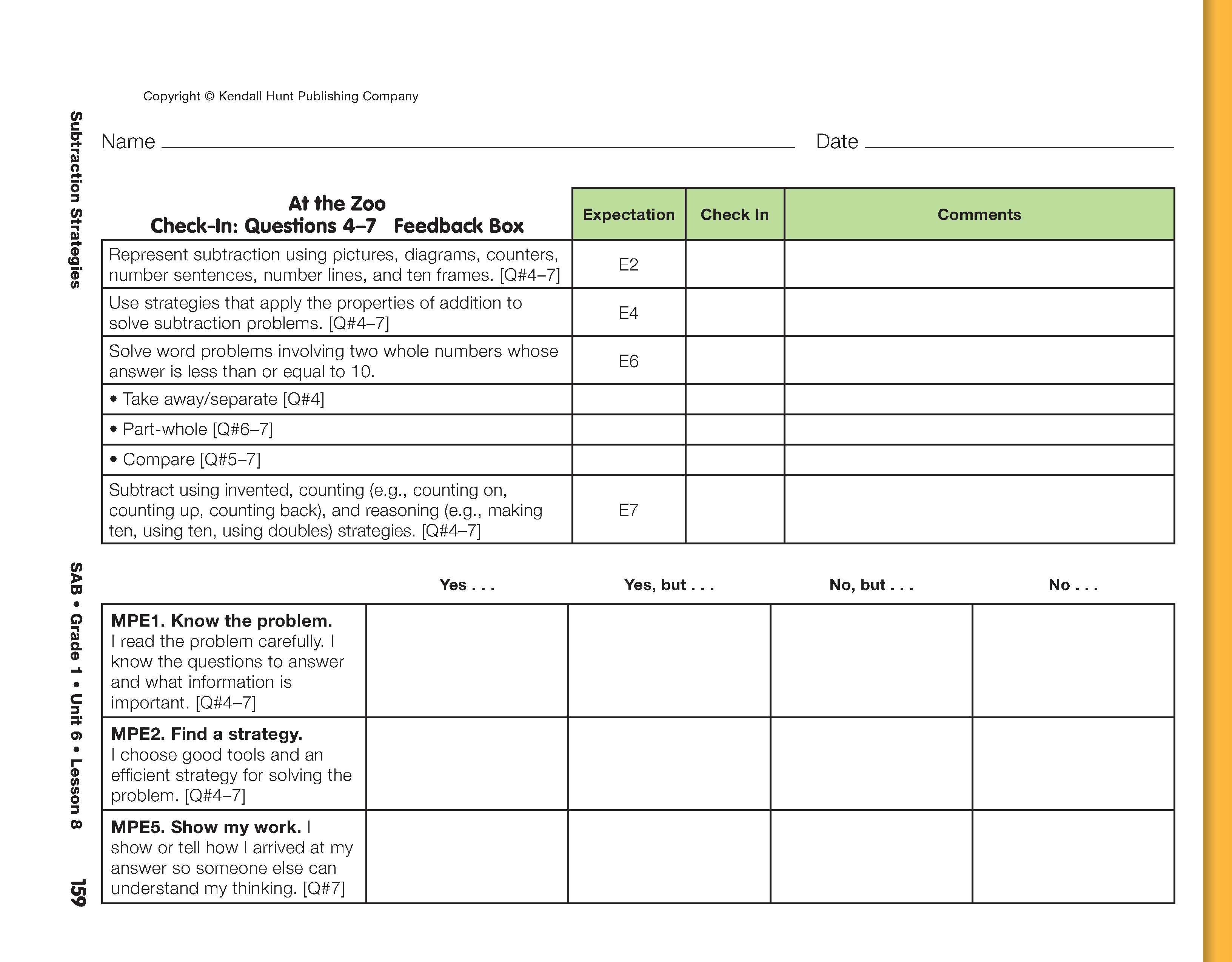
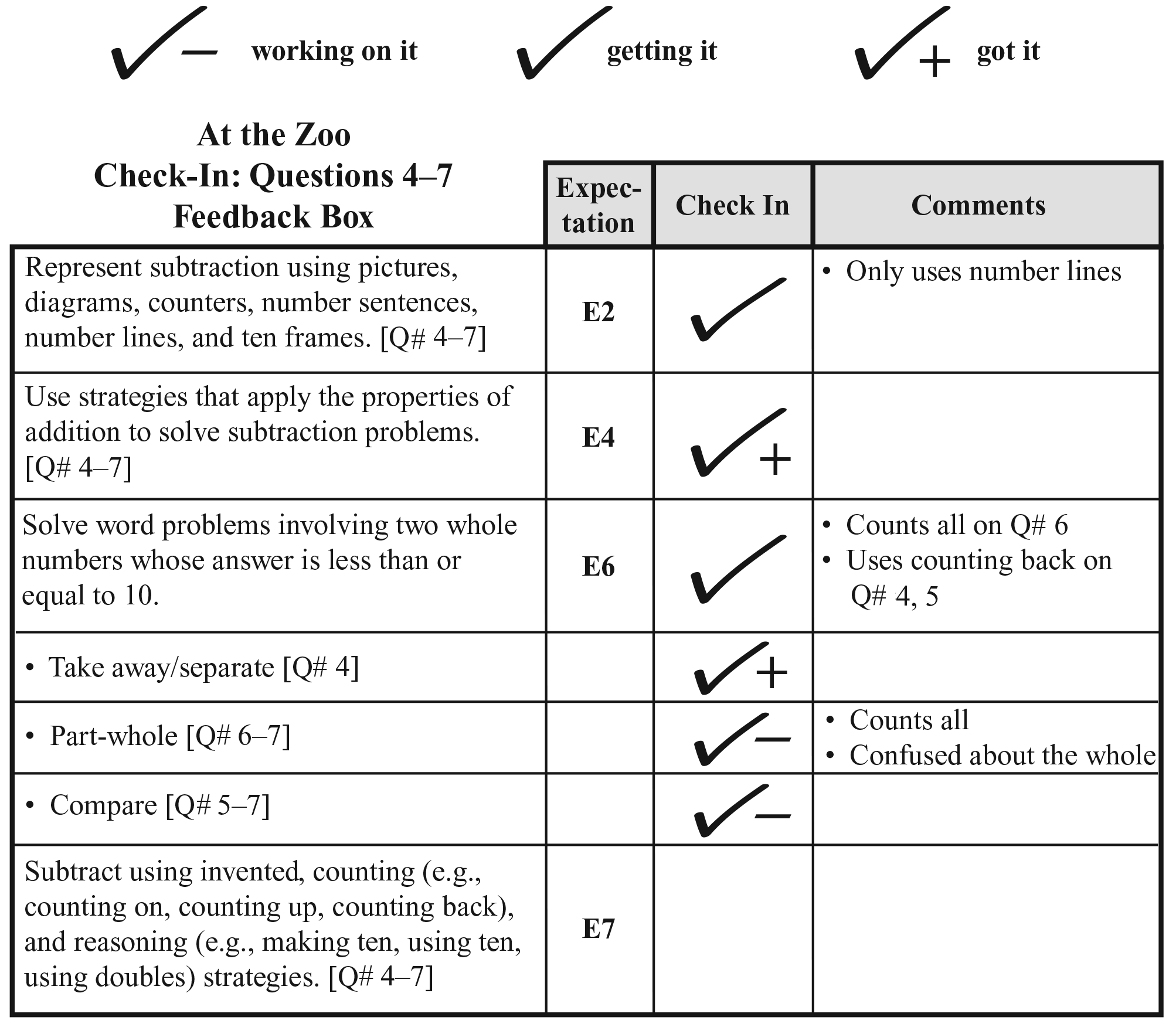
Use Check-In: Questions 4–7 on the At the
Zoo pages in the Student Activity Book and the
Feedback Box to assess students' abilities to represent
subtraction using stories, drawings, diagrams, counters, number
sentences, number lines, and ten frames [E2]; use strategies
that apply the properties of addition (e.g., turn-around) to
solve subtraction problems [E4]; solve word problems (e.g.,
separate/take away, part-whole, or compare) involving two whole
numbers whose answer is less than or equal to 10 [E6]; subtract
using invented, counting (e.g., counting on, counting up,
counting back), and reasoning (e.g., making ten, using ten,
using doubles) strategies [E7]; know the problem [MPE1]; find a
strategy [MPE2]; and show work [MPE5].
See Figure 6 for an example of a completed Feedback Box.