Explore Turn-Around Facts. Ask students to look
at the Sorting Mat comple ted by the group who
worked on the chart paper. See Figure 4.
Explain that each group on the chart shows different
ways to name the same number.
- Look at the Sorting Mat. What are all the ways we found to name five on our chart? (5 + 0, 4 + 1, and
3 + 2)
- Each number sentence names two numbers that can be combined to make 5. What are all the pairs of numbers that combine to make five? (0 and 5, 4 and 1, 3 and 2)
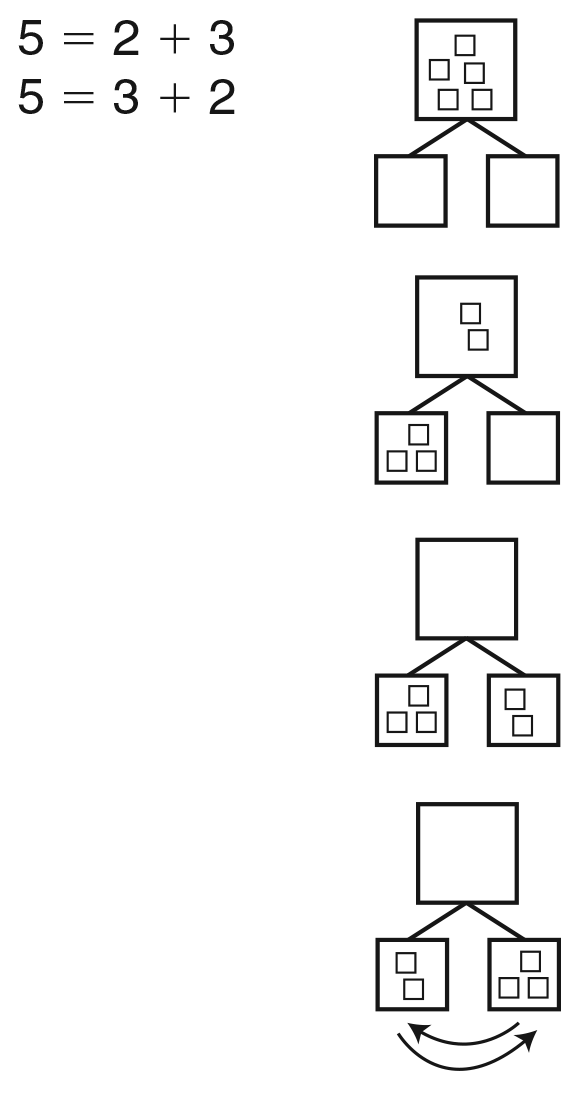
Display the Box Diagram Master. Explain that this is
a new diagram, similar to the part-whole diagram.
Model the addition sentences for 5 on this diagram
with connecting cubes. See Figure 5.
- Look at the pairs of numbers that make five. Five
is the whole. Where do you think the 5 goes? (The
5 cubes should go in the large box.)
- One of the ways to make five is 3 + 2. How can we
show the 3 in that number sentence? (Move 3
cubes from the large box to the small box on the
left.)
- How can we show 2 in that number sentence?
(Move the remaining 2 cubes to the other small
box.)
- How could we write this same problem using numbers
in this diagram? (5 in the large box, 2 and 3
in the two smaller boxes.)
- If I switch the 2 and the 3, will that still make 5?
(yes)
- How could we write this problem using numbers in
this diagram? (5 in the large box, 2 and 3 in the
two smaller boxes.)
When using cubes to model problems in part-whole diagrams,
remember to use no more than the total number of cubes (the
whole) at any one time as shown in Figure 5.
Follow the same procedure for 4 + 1 and 5 + 0.
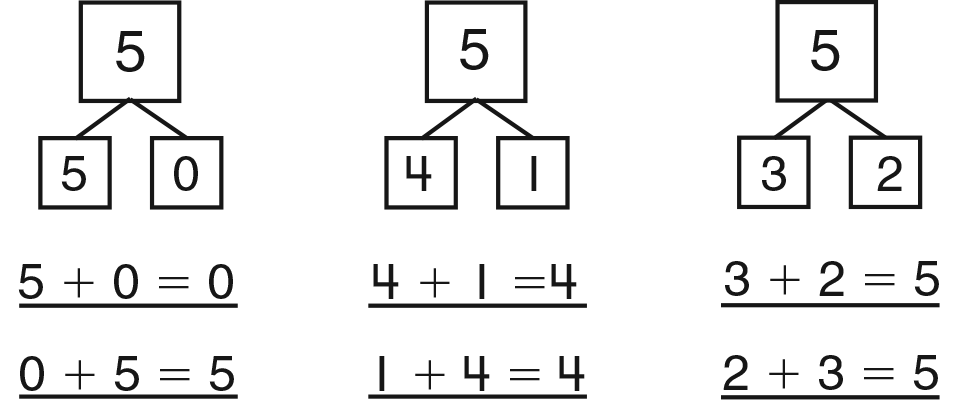
Display the Partitions of Five Master. Tell students
that they can use box diagrams to show each pair of
numbers that can be combined to make five. After
showing them the diagrams and the related number
sentences from the cards, explain that the order of
the two numbers in the small boxes can be reversed
or turned around. This is called a turn-around fact.
- If you know that five plus zero is equal to five, you
also know that zero plus five is equal to five. This
is called a turn-around fact. What are the other
turn-around facts for five? (1 + 4 and 2 + 3)
Record the turn-around facts for five on the Master. See
Figure 6.
Commutative Property of Addition. The commutative property
of addition says that the order in which the addends are added
does not affect the sum of the problem. Both 2 + 3 and
3 + 2 equal 5. When two numbers are added, the sum is the
same regardless of the order of the addends.
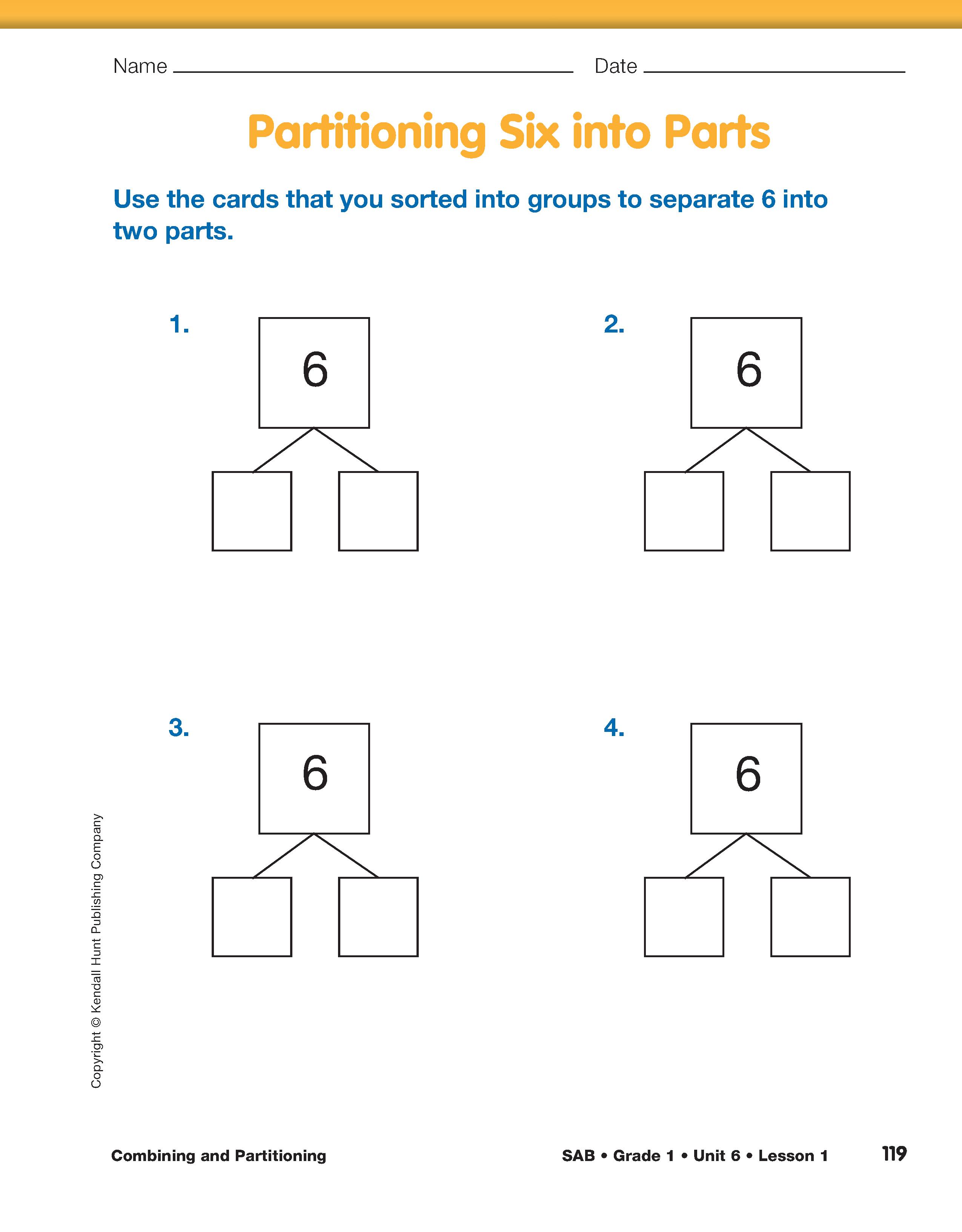
Ask students to work with their partner to complete
Questions 1–4 on the Partitioning Six into Parts
page in the Student Activity Book. Direct them to use
Questions 1–4 on the Partitioning Six into Parts
page in the Student Activity Book. Direct them to use
the completed Sorting Mats to complete the page.
Ask students to share their work as you record their
partitions and the related number sentences on the
display of the Partitioning Six into Parts page.
For each suggested partition, ask:
- What is a number sentence that represents your
first partition of six? (Possible response for a partition
of 5 and 1: 5 + 1 = 6)
- What is the turn-around fact for 5 + 1 = 6?
(1 + 5 = 6)
- I see that one of the partitions of 6 is 3 and 3. What
number sentence represents this partition of six?
(3 + 3 = 6)
- Is there a turn-around fact for this partition? (no)
Why? (Possible response: Since both of the partitions
are three the turn-around fact would be the
same.)
- Look at the Sorting Mat. What are some other numbers
that can be partitioned using doubles?
(2, 4,
8, and 10)
- What do you notice about all of those numbers?
(They are all even numbers.)
Continue this discussion until all of the partitions of
6 have been shared.
Addition with Zero and Using Known Facts. Ask
students to look at the completed Sorting Mat on display
and find all of the problems with zero in them.
- What are all of the problems on our chart that have
a zero as one of the partitions? (0 + 0, 1 + 0,
2 + 0,
3 + 0, 4 + 0, 5 + 0, 6 + 0, 7 + 0, 8 + 0,
9 + 0, 10 + 0)
- What pattern will help you solve these problems?
(Possible response: I notice that the answer is
always the same as the number you are adding to
zero.)
- What do we call the answer to an addition
problem? (sum)
- Right, the answer to an addition problem is called
a sum. Can someone describe the pattern
[student name] found using the word sum?
(Possible response: When you add zero to a number
the sum is the same as the other number in
the problem.)
- Let's think about the number sentence 9 + 0. If
you know that 9 + 0 = 9, what other fact do you
know?
(0 + 9 = 9) Why? (Possible response:
When you are adding two numbers you can turn
the numbers around and the answer will still be
the same.)
Tell students that thinking about turn-around facts and
adding with zero will help them solve problems with addition.
Explain that they can also use facts they already know to help
them find the answer to other problems. Have students find all
of the number sentences on the Sorting Mat for the sum of ten.
- Choose one of the number sentences with a sum
of 10. How did you decide that it went with this
group? (Possible response: I put 6 plus 4 in the
group with a sum of 10. I thought about a ten
frame with 6 dots and 4 empty spaces.)
- How can you use 6 plus 4 to help you find 6 plus
3? (Possible response: Six plus three will be one
less than six plus four, so the sum will be nine.)
- Tell how you can use 6 + 4 to help you solve five
plus four. (Possible response: Five plus four will
also be nine because five is one less than six.)
- Let's try another problem with a sum of ten. Tell
how you can use 8 + 2 to help you find the answer
to 8 + 3. (Possible response: Eight plus three will
be eleven because it is one more than ten.)
Remind students that they have learned many strategies
that can help them solve addition problems.
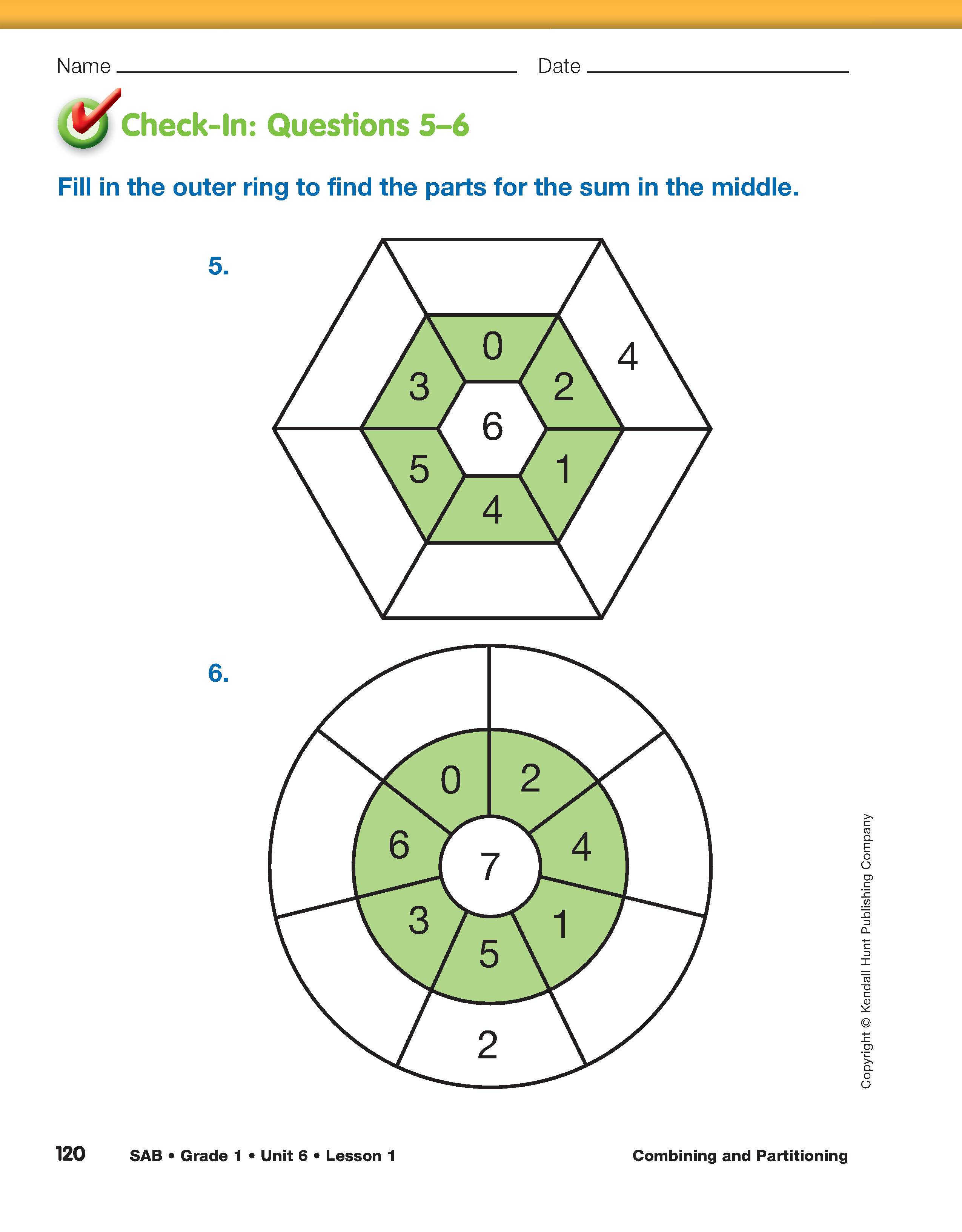
Ask them to think about these strategies as they
complete Check-In: Questions 5–6 on the
Partitioning Six into Parts pages in the Student
Activity Book. Display the questions and review the
directions before students begin their work. Observe
students as they are working and ask them to
describe the strategies they are using.
Use Check-In: Questions 5–6 on the Partitioning Six into
Parts pages in the Student Activity Book and your observations
as they work to assess students' abilities to add within ten
using invented, counting, and reasoning strategies [E7].
Use the Practicing Addition Facts Homework Master from
Lesson 2 or the Addition Practice Menu from Lesson 5 to provide
targeted practice with the addition facts [E7].