Add and Subtract to Solve Problems
In this unit, students focus on further developing their understanding of the addition operation. Students focus on developing a variety of strategies and tools to solve single-digit addition problems, the math facts. Students also demonstrate the connections between addition and subtraction and discuss some of the properties of addition (e.g., turn-around facts, fact families, addition of zero). Students encounter the various types of problems in different contexts and first model the problems directly before developing more efficient counting strategies for the addition facts with sums to ten.
“Children come to understand the meaning of addition in the context of word problems”
(National Research Council, 2001).
Developing Addition Strategies
Students come to understand the concept of addition by interpreting and finding strategies ... read more
Developing Addition Strategies
Students come to understand the concept of addition by interpreting and finding strategies to solve different types of problems (e.g., join, separate, compare, and part-whole). As they do, they also develop greater fluency with each specific counting strategy. Significant research from all over the world indicates that children move through a progression to find the sum of single-digit numbers. First, children count all objects, then count on, and then they reason the sum from known facts. See Figure 1. (National Research Council, 2001; Fuson, 1992)
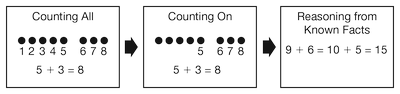
Work in previous units developed these ideas. In Unit 3, students partitioned numbers into two parts using trains of cubes, part-whole diagrams, ten frames, and number sentences. Particular attention was paid to representing the partition of ten using ten frames so that students could build a strong visual image of the sums to ten.
In Unit 4, students explored counting strategies for addition using varied contexts including word problems, part-whole diagrams, and number lines. In this unit, students focus on devising strategies for the addition facts with sums to ten. They solve problems and share strategies with their peers. In this way, students can develop more mature strategies that they can later apply to addition facts with larger numbers.
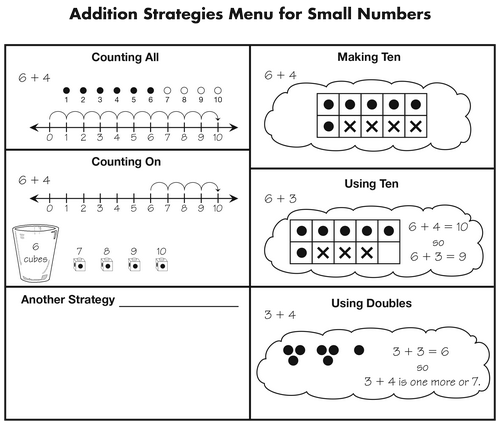
Students may choose different strategies for different problems and may gravitate to some strategies and not to others. Some problem types will lead students to use certain strategies and others will lead to a variety of strategies. It is important to give students time to invent and explore a variety of strategies. Students proficient with addition can choose from a collection of strategies and think critically about the advantages of one strategy over another. As students gain more experience and confidence with these different strategies, they will gain fluency and flexibility. To encourage them to think about the appropriateness of a strategy, you will have students summarize and formalize their invented strategies into an Addition Strategies Menu for Small Numbers in Lesson 5. See Figure 2.
Subtraction Concepts
This unit develops subtraction concepts by building on students' natural understanding of subtraction just as Unit 4 ... read more
Subtraction Concepts
This unit develops subtraction concepts by building on students' natural understanding of subtraction just as Unit 4 Adding to Solve Problems built on students' understanding of addition. However, there are important differences in the degree of complexity that addition and subtraction pose for students. Their everyday and kindergarten experiences generated a strong foundation for addition. Subtraction, on the other hand, is less conceptually established. This unit builds subtraction concepts, language, and skills that help students make sense of subtraction situations in order to solve problems.
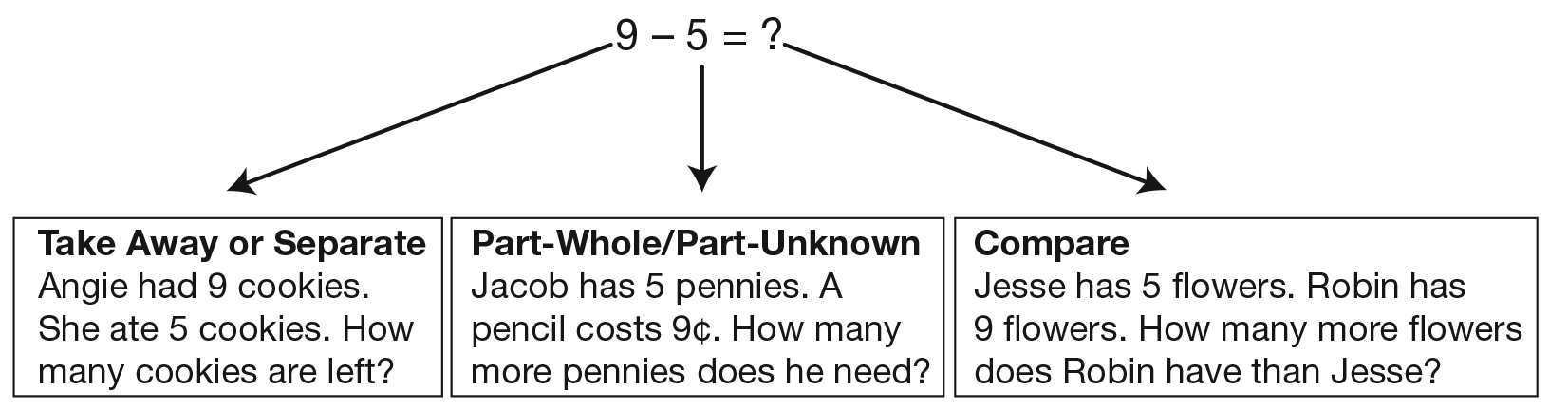
Three main types of problem situations that can be represented by 9 − 5 = ? are illustrated in Figure 3.
It is important that students encounter multiple examples of each of the three main subtraction situations—Take Away or Separate, Part-Whole/Part Unknown, and Compare—so that they can learn to choose appropriate strategies and tools to solve all kinds of problems. Students need not learn to identify or name the types of problems. Rather, they need to learn to approach all types of problems with confidence. As students work on problems, focus on the way they reason to find answers and on the language and representations they use to describe their thinking.
Developing Subtraction Strategies
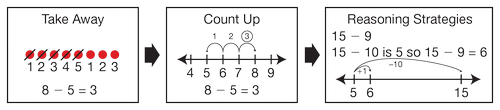
The learning progression for subtraction is similar to that of addition. See Figure 4. ... read more
Developing Subtraction Strategies
The learning progression for subtraction is similar to that of addition. See Figure 4. Students invent counting-back strategies that model the taking away problem situation. Some invent counting-up strategies for some situations in compare or missing addend situations. Focusing students on part-whole relationships also help students develop reasoning strategies, especially for subtraction. These experiences help students connect addition and subtraction and help them recognize when to add and when to subtract. "For students in grades K to 2, learning to see the part-whole relations in addition and subtraction situations is one of their most important accomplishments in arithmetic." (National Research Council, 2001)
Connect Addition and Subtraction
There are many opportunities in this unit to connect addition to subtraction. ... read more
Connect Addition and Subtraction
There are many opportunities in this unit to connect addition to subtraction. Students connect join situations to take away situations by using addition and subtraction to solve compare situations. Students also make this connection by using addition and subtraction to represent and solve problems involving the missing addend. For example, in Lesson 4 All about Ten students use the ten frames to see the relationship between the numbers 6 + 4 = 10 and 10 − 4 = 6. See Figure 5.
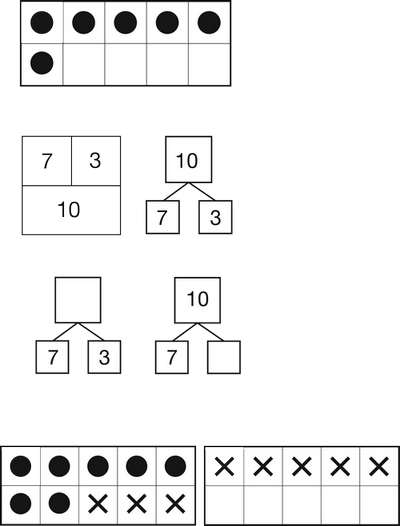
Exploring the relationship between addition and subtraction lays the foundation for learning the subtraction facts. For example, if a student is asked to find the difference between 15 and 7, the problem can be interpreted as 7 + = 15. Understanding the relationship between addition and subtraction greatly reduces the number of new facts to learn. It also provides students with a method for checking their own calculations.
Representations
The box diagram is introduced in this unit to facilitate the representation of addition and subtraction. ... read more
Representations
The box diagram is introduced in this unit to facilitate the representation of addition and subtraction. It is a dynamic model that helps students interpret and represent combining (composing) numbers and separating (decomposing) numbers. It is similar to the part-whole diagram used in earlier units. See Figure 6. The numbers that result from decomposing a number are often called partitions.
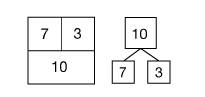
The part-whole diagram shows the two parts (7 and 3) of the whole (10). The box diagram shows that we can combine 7 and 3 to make ten or separate 10 into two parts, 7 and 3. See Figure 7.
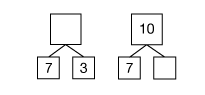
These diagrams are often used to help students visualize ways to flexibly take apart and put together numbers to add and subtract. For example, to add 7 + 8, students can mentally decompose 7 into 5 and 2, so that 7 + 8 becomes 5 + 2 + 8 or 5 + 10.
Ten frames can be used in a similar way to visualize the addition of 7 + 8 as shown in Figure 8 (National Research Council, 2001).
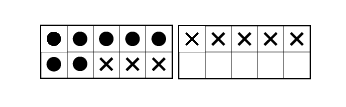
Flexible use of representations such as these develop conceptual understanding and support use of tools and strategies to solve problems. Experiences with these representations serve to develop strong number sense. That is, they provide opportunities for students to acquire "a variety of abilities and understanding that include an awareness of the relationships between numbers, an ability to represent numbers in a variety of ways, a knowledge of the effects of operations, and an ability to interpret and use numbers in real-world counting and measurement situations" (National Council of Teachers of Mathematics, 1993).
MATH FACTS and MENTAL MATH

In accordance with the Principles and Standards for School Mathematics (NCTM, 2000), the ... read more
In accordance with the Principles and Standards for School Mathematics (NCTM, 2000), the Curriculum Focal Points (NCTM, 2006), and the Common Core Standards for Mathematics (Council of Chief State School Officers, 2010), Math Trailblazers students are expected to achieve fluency with the addition and subtraction facts by the end of second grade. They work toward this goal in Grade 1 by solving addition and subtraction problems in ways that make sense to them. Students also focus on developing fluency with the addition facts with sums to ten first, as fluency with these facts will help students develop strategies for the facts with larger sums. This use of meaningful strategies enables students to understand the operations, while at the same time developing fluency with the math facts.
The goal of the math facts development in Math Trailblazers is for students to learn the basic facts efficiently, gain fluency with their use, and retain that fluency over time. A large body of research supports an approach in which students develop strategies for figuring out the facts rather than relying on rote memorization. This not only leads to more effective learning and better retention, but also to the development of mental math skills. In fact, too much drill before conceptual understanding may interfere with a student's ability to understand concepts at a later date.
The research that contributed to the National Council of Teachers of Mathematics' Principles and Standards for School Mathematics and the National Research Council's Adding It Up has informed the structure of the math facts strand in Math Trailblazers. See the Letter Home for more about the development of the basic facts in 1st-grade Math Trailblazers.
Addition Facts with Sums to Ten
This unit begins the systematic review and assessment of students' fluency with the addition facts with ... read more
Addition Facts with Sums to Ten
This unit begins the systematic review and assessment of students' fluency with the addition facts with sums to ten and then all the addition facts. Students will practice the facts in small groups. The facts in each group can be solved using similar strategies. See Figures 9 and 10. In this unit, students will have the opportunity to gain fluency with the addition facts in Groups A and B. Students will use counting strategies and apply the properties of addition (e.g., turn-around facts, adding zero) to solve these facts.
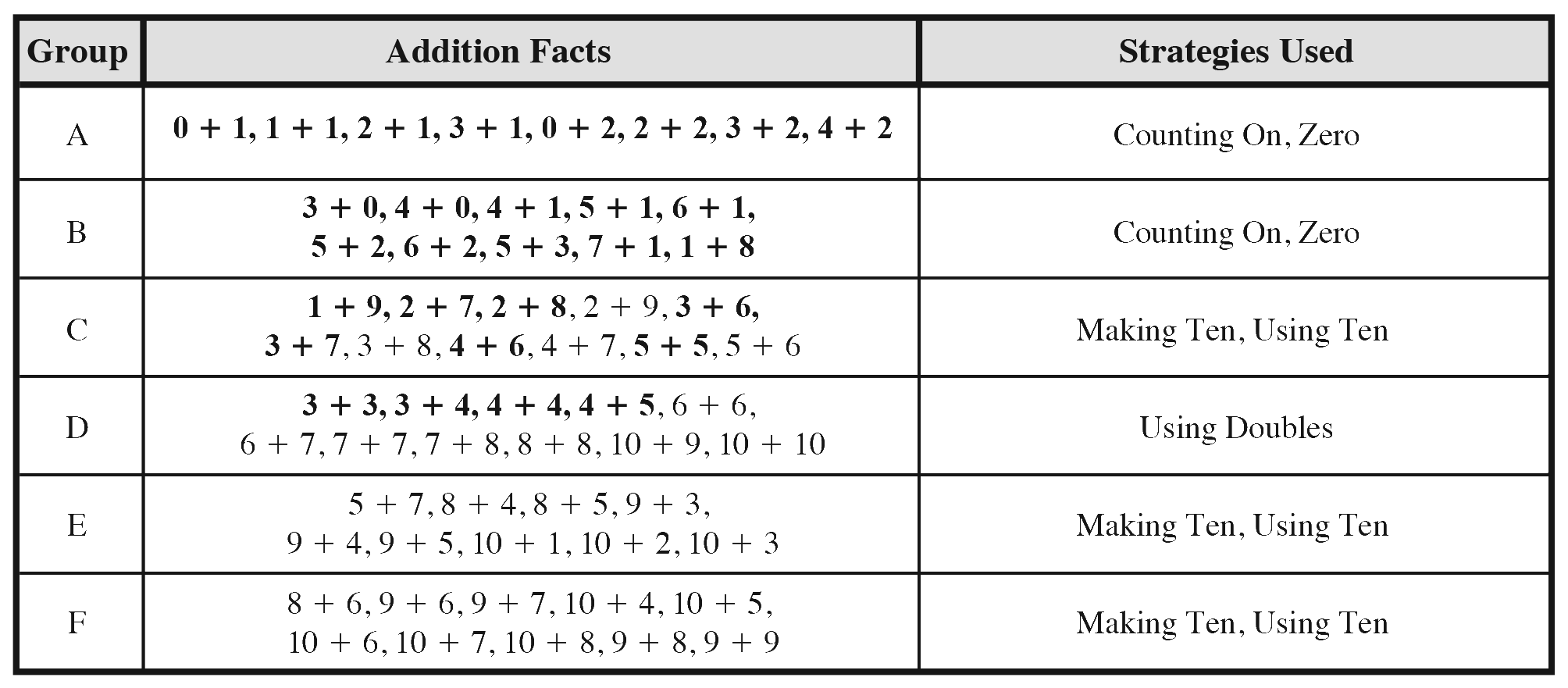
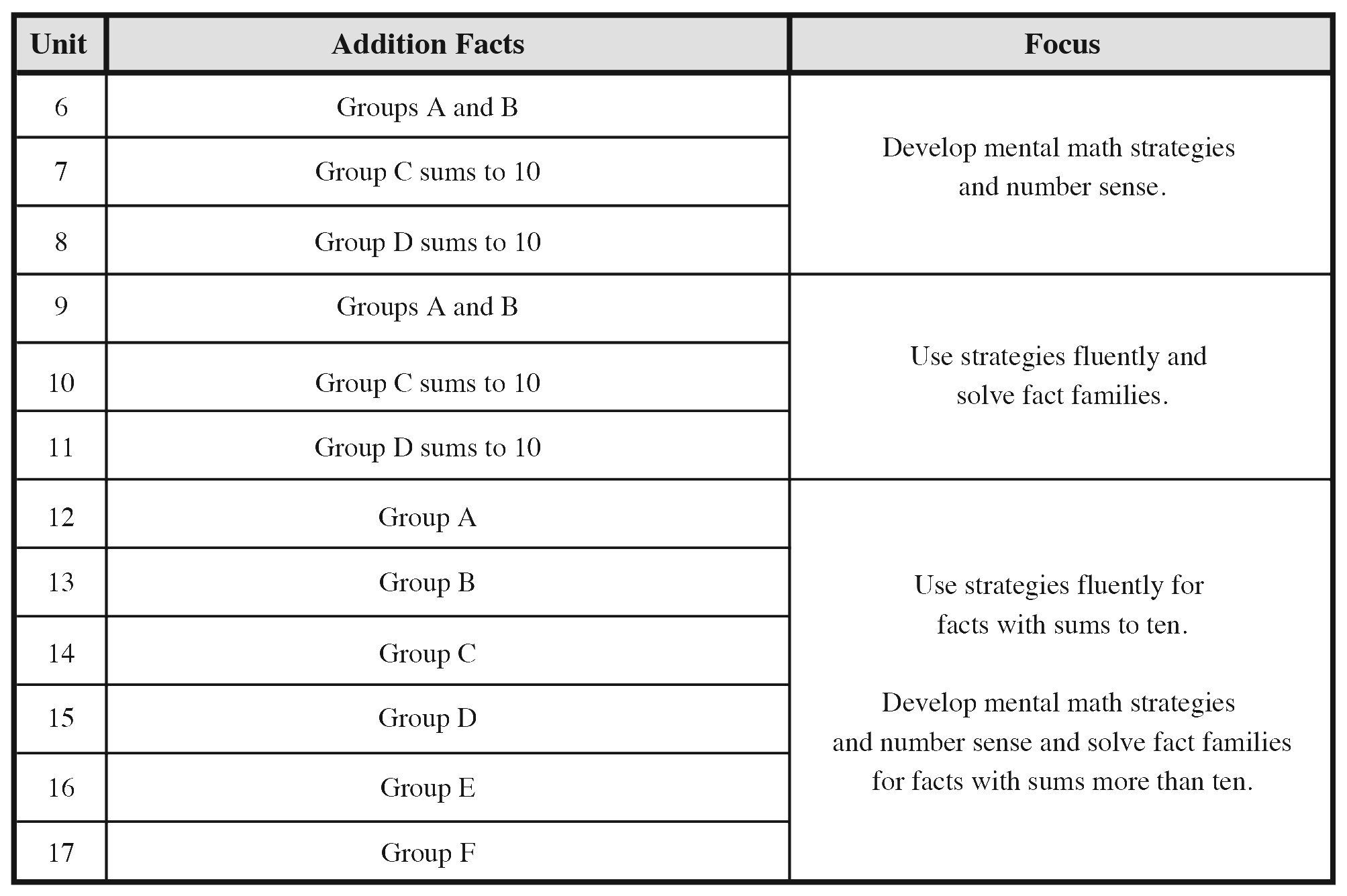
Resources
- Baroody, A.J. “Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them.” In Teaching Children Mathematics 13(1), 22–31. National Council of Teachers of Mathematics, Reston, VA, 2006.
- Burton, G. M., with A. Mills, C. Lennon, and C. Parker. Curriculum and Evaluation Standards for School Mathematics: Addenda Series, Grades K–6: Number Sense and Operations. National Council of Teachers of Mathematics, Reston, VA, 1993.
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH, 1999.
- Common Core State Standards for Mathematics. National Governors Association Center for Best Practices, Council of Chief State School Officers, Washington, DC, 2010.
- Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherence. National Council of Teachers of Mathematics, Reston, VA, 2006.
- Fuson, K. C. “Research on Whole Number Addition and Subtraction. ” In Handbook of Research on Mathematics Teaching and Learning. D. Grouws, ed., 243–275. New York: Macmillan, 1992.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- National Research Council. Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Research Council. “Teaching for Mathematical Proficiency.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Takahashi, A., T. Watanabe, and M. Yoshida. Elementary School Teaching Guide for the Japanese Course of Study: Arithmetic (Grades 1–6). Unofficial translation of Elementary School Teaching Guide: Arithmetic, Japanese Ministry of Education, Culture and Sports, 1989. Global Education Resources, L.L.C., Madison, NJ, 2004.
- Thornton, C.A. "Strategies for the Basic Facts." In Mathematics for the Young Child. J.N. Payne, ed. The National Council of Teachers of Mathematics, Reston, VA, 1990.
- Van de Walle, J.A., and L.H. Lovin. Teaching Student-Centered Mathematics: Grades K–3. Pearson Education, Boston, 2006.












