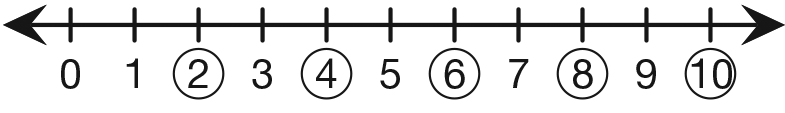Review Repeating Patterns.
Begin the activity by
reviewing repeating patterns. Display a pattern such
as:












- What can you tell me about this pattern? (Possible
response: The pattern is triangle, square, square,
circle, triangle, square, square, circle.)
- What is the pattern unit for this pattern? (triangle,
square, square, circle)
- Describe how you find the pattern unit. (Possible
response: Look to see what part of the pattern
gets repeated.)
- What comes next in this pattern? (triangle)
- How would you describe this pattern using alphabet
shorthand? (ABBCABBC)
Growing Patterns That Increase. Explain to students
that they will learn about a new kind of pattern.
Show the trains of connecting cubes you
prepared with 1 and 2 cubes.
- Now we are going to learn about a new kind of pattern.
What do you think will come next? (3)
Students might focus on color but continue to show
trains of connecting cubes with 3, 4, and 5 cubes.
They may begin to see that the pattern concerns
number and not color.
After displaying the train of 5 cubes, ask:
- What do you think comes next? (6)
Students might be surprised to see that the color of
the sixth cube in the train is changed, but explain
that you changed the color to make the cubes easier
to count. Have students predict what comes next
until you reach the train of 10 cubes. Once students
have recognized that the pattern is counting by ones,
explain that this is called a growing pattern.
Explain that a growing pattern changes in a way that
we can predict. In the pattern of counting numbers,
we can predict which number comes next by adding
"one" to the previous number. See the Mathematics
in this Unit section for more information.

A growing pattern can either increase or decrease with each
successive component, even though the term implies that the
numbers get larger. As noted in the definition, a growing
pattern is characterized by a consistent arithmetic change
between any two adjacent components. A pattern in which
there is no change is a repeating pattern. It is the characteristic
of change that defines a growing pattern. This change may be
by subtraction or division, as well as by addition or
multiplication. A consistent arithmetic change of, say, subtract
two, will result in a pattern of decreasing numbers. According
to the definition, this is a growing pattern. The important thing
is for students to be able to recognize a simple number pattern
and extend it correctly, whether the numbers are increasing or
decreasing.

As you display the trains of connecting cubes, use self-adhesive
notes to record the number of connecting cubes in
each train. Students may see the patterns more easily with the
numbers displayed near each train.
Repeat the activity, this time displaying the trains of
2 cubes, 4 cubes, 6 cubes, 8 cubes, and 10 cubes.
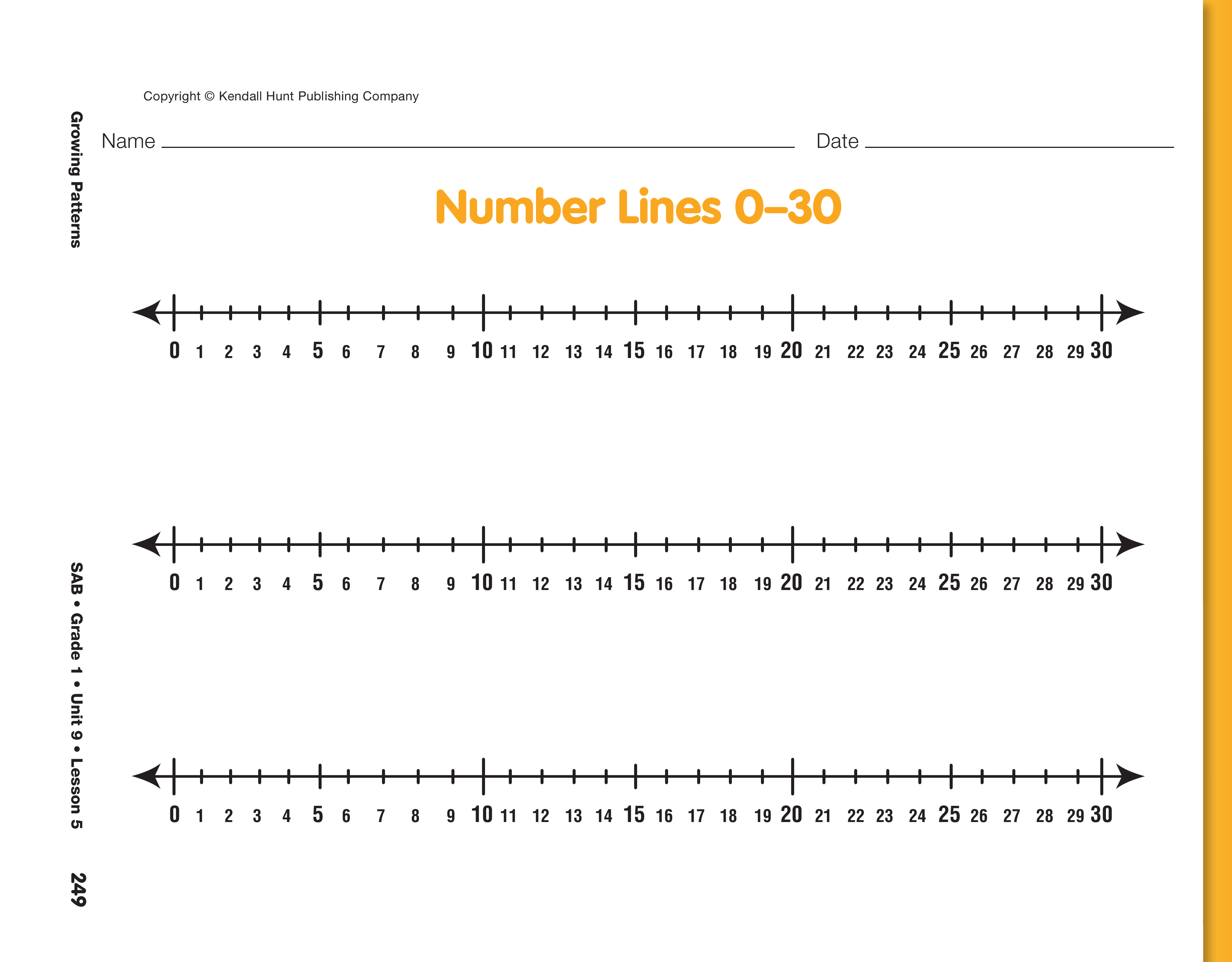
Refer students to and display one of the number lines
on the Number Lines 0–30 pages in the Student
Activity Book. Represent the cube pattern by circling
the numbers on the number line. Ask students to do
the same on their number lines. See Figure 2.
- What is this pattern? (2, 4, 6, 8, 10. It's even numbers,
counting by twos.)
- What is the rule for this pattern? How can we predict
what the next number will be? (Possible
response: Add two to the number before. Start at
2 and skip every other number.)
- What number will come next? (12)
- How do you know? (Possible response: I added 2
to 10, because we left off at 10.)
Repeat the activity and the discussion with odd numbers
with trains of 1 cube, 3 cubes, 5 cubes, 7 cubes,
and 9 cubes. Represent the pattern with the connecting
cubes and on a number line. Use a different number
line on the Number Lines 0–30 pages so that later
you can compare the patterns.
- What pattern is this? (1, 3, 5, 7, 9; odd numbers;
skip counting by 2s)
- How is this pattern the same as the even numbers?
(Possible response: You count on two each
time to get the next number.)
- How is it different from the even numbers? (It
starts at a different number.)
- What does this pattern look like on the number
line? (Every other number is marked but starting
with one.)
Repeat with trains that have lengths that are multiples
of fives: 5, 10, 15, 20, 25, and 30. Represent the
pattern with connecting cubes, numbers, and then by
circling the number on the number line. Have students
volunteer other growing patterns and show
them on the number line.
Growing Patterns That Decrease. Next, try the
activity with decreasing numbers. Start by showing
trains of 10 cubes, 9 cubes, 8 cubes, and so on.
- What pattern is this? (10, 9, 8, 7; counting down
by one)
- What comes next? (6, 5, 4)
- How do you know? (6 is one less than 7.)
- What does this pattern look like on the number
line? (Every number is marked but starting with
10.)
Repeat this discussion and these representations with
other decreasing patterns. Try a few more such as:
9, 7, 5, 3, 1
14, 12, 10, 8, 6, 4, 2, 0
30, 25, 20, 15, 10, 5, 0
See the Sample Dialog to guide your discussion of
growing patterns that decrease by twos.

Use this Sample Dialog to discuss growing patterns that
decrease.
Teacher: [displaying the trains of 14 cubes, then 12 cubes,
10 cubes, etc.] What is happening now?
Alex: The trains are getting smaller.
Teacher: Who can predict what is next in this pattern?
Samuel: Eight is next, because it's going backward, 14, 12,
10, then 8.
Teacher: But why wouldn't the next number be 9 since I'm
going backward?
Samuel: Because you're going backward by twos. It's like
you're counting by twos by going backward.
Teacher: That's right, Samuel. What do you think my next
train of connecting cubes will be?
Nicole: I think it will be 6.
Teacher: How did you figure that out, Nicole?
Nicole: I started at 8 on my number line and I moved back
two: 7, 6. I got to 6.
Teacher: That's a great strategy, Nicole. When the
numbers are getting smaller, we count back on the
number line. Do you think this is a growing pattern?
Roberto: I think it's a shrinking pattern.
Teacher: We call this shrinking pattern by the same name:
growing pattern. I guess we say the numbers are
growing smaller instead of growing larger. The
important thing to remember is that each new part of
the pattern has to change from the one before it.