Lesson 7

Patterns on the 100 Chart

Est. Class Sessions: 2–3

Developing the Lesson

Part 2: Patterns on the 100 Chart

Skip Count on the 100 Chart. Direct students' attention to the display of the 100 Chart page from the Student Activity Book. Give students a few moments to look over the 100 Chart page.

Ask:

X
  • What is different and what is the same about the 50 Chart and the 100 Chart? (Possible response: They are the same except the 100 Chart includes more numbers.)

Students count along with you as you skip count by twos to 40 starting with 2. Then repeat the count, but this time ask students to place a connecting cube on each even number as they say it. Use a highlighter to shade the corresponding numbers on the display of the 100 Chart.

When they finish counting by twos and placing the cubes, ask:

X
  • Do you see any patterns on the chart? (Possible responses: The cubes are in 5 columns, every other column, under the numbers 2, 4, 6, 8, 10.)
  • Have we learned a name for the numbers we covered? (the even numbers)
  • Will we cover the number 52 if we continue counting? (yes)
  • How about 76? (yes) 80? (yes) 85? (no)
  • How do you know? (Possible responses: The even numbers are in columns; the last number is either a 2, 4, 6, 8, 0.)
  • What are some other numbers that we would cover? (See Figure 3.)
  • Are these all even numbers? (yes)

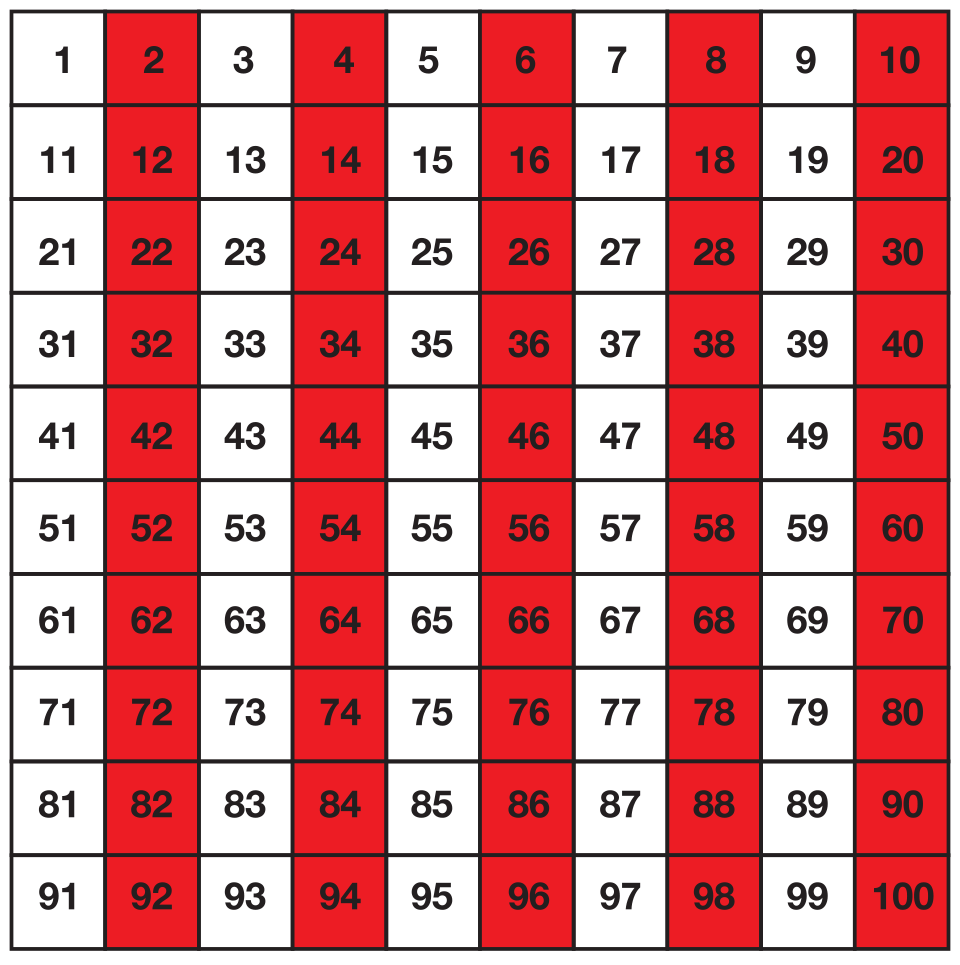
Remove the cubes from the chart and repeat the same procedure, including placing cubes on the 100 Chart as you skip count, this time counting by fives to 50. See Figure 4.

Ask:

X
  • What patterns do you see now? (Possible responses: Two columns going down. All the numbers in the first column that is covered end in five. All numbers in the last column end in zero.)
  • Will we cover 85 if we continue counting? (yes)
  • How do you know? (Counting by fives ends in a five or zero and 85 ends in 5.)
  • Will we cover 73? (no)
  • How do you know? (Counting by fives ends in a five or zero.)
X

When the class is discussing the patterns that arise on the 100 Chart when the multiples of five are shaded, compare the chart with a name-grid from Lesson 4 of a student who has five letters in his or her name. Ask how the two charts are alike and different. Help students make connections between shading the fifth letter of the name and skip counting by five.

Compare Name Grid Pattern to Skip Counting by Fives. Display the Name Grid from Lesson 4 with the five-letter name you prepared.

Discuss how the pattern made by the 5-letter name is similar to the pattern made by skip counting by five on the 100 Chart.

X
  • Look at [Steve's] name on the Name Grid. How is the name pattern similar to the 100 Chart when we counted by fives? (Possible response: They are exactly the same.)
  • Why do you think they are the same? (Possible response: Since [Steve's] name has five letters I am counting by fives to shade in the last letter in his name. When I am skip counting I am also counting fives though I am not saying the numbers in between.)

Skip Count by Tens. Clear the 100 Chart and have students count along with you as they skip count by tens to 100. Before beginning to skip count, have students count with you by ones until they reach 10. Then have students place a cube on 10. Count 10 more together, starting at 11 until they reach 20. Then place a cube on 20. Count 10 more, starting at 21 until they reach 30. Then place a cube on 30. Continue to count this way until they reach 100, placing a connecting cube on each ten (number) as they say it. 10, 20, 30, 40 …100. Students count a second time by tens to 100, tapping the cubes as they count: 10, 20, 30, 40, 50 …100.

When they finish counting by tens, ask:

X
  • What pattern do you see now? Describe the pattern. (Possible response: One column has cubes, down the last column.)
  • How many total cubes have you placed on your 100 Chart? (10)
  • Where are they located? (in the last column)
X

If necessary, have students build ten trains of 10 cubes each and place them on the 100 Chart. Count by tens, tapping each train of ten as you say the numbers counting: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100. Point out to students that ten trains of 10 is 100 cubes; 10 tens is the same as 100..

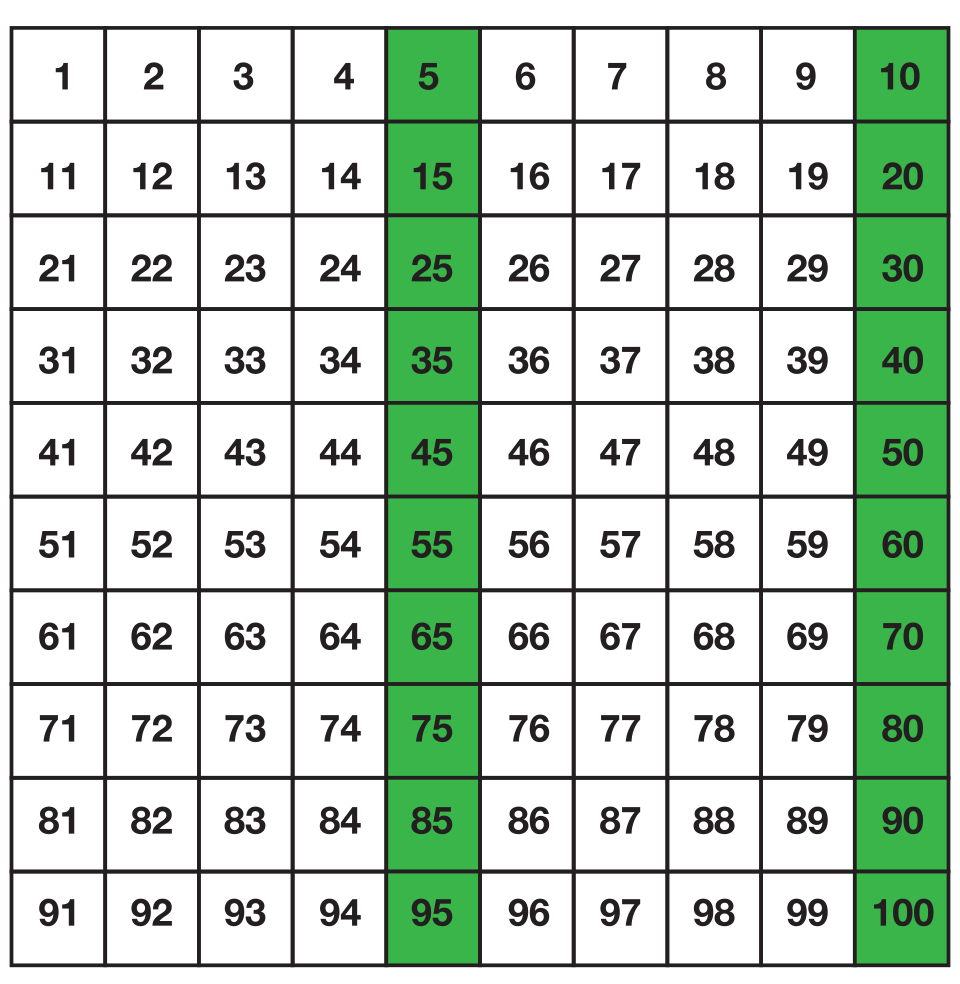
Skip Count by Tens Starting with Four. Ask student pairs to make a train of four cubes and then ask them to place a cube on the number 4 on the 100 Chart. Next have them build one train of ten cubes and set it next to the train of four cubes. Ask them to identify the total number of cubes by placing a cube on the 100 Chart. Have students place a cube on 14 on the 100 Chart.

Ask:

X
  • If we add another train of ten cubes, how many cubes will we have? (24)
  • Show me how you know. (I took apart my train of 10 cubes and placed it on the chart after 14. The last number it covered was 24.)

Ask students to continue to add 10 more and identify the number by placing a cube on the number chart until they reach 94. See Figure 5.

Ask:

X
  • Describe the pattern you see. What do you notice about the numbers you have covered? (Possible response: One column straight down; all the numbers end in 4, only the first number changes by one.)
  • If we placed a cube on every number on the chart, how many total cubes would fit? (100)

Display each of the 100 Charts you shaded in during the discussions in this lesson. List on chart paper the number patterns they can identify. See the Sample Dialog.

Ask:

X
  • We discovered a number of patterns when we counted on the 100 Chart. What are some of the patterns we discovered? (Possible responses: When counting by fives, we have two columns going down from the 5 and the 10; when we count by tens, the last column is filled in: 10, 20, 30, etc.; when we count by twos, we have 5 columns going down starting with 2, 4, 6, 8, 0.)
X

Use the Sample Dialog to guide your discussion of patterns on the 100 Chart.

Teacher: Let's make a list of the patterns we discovered on the 100 Chart.

Keenya: All the numbers at the end of the rows end in zero.

Teacher: That's true. What do we call those numbers?

Keenya: The tens.

Teacher: Yes, so 20 is how many tens?

Keenya: Two tens. And 30 is 3 tens and 40 is 4 tens.

Teacher: Very good. Let's write that on the board. [Writes "tens are at the end of the rows; the last number in the tens is always 0."] Who else can remember a pattern we talked about?

Nicholas: If you go across, it's like counting. 1, 2, 3, 4, like that.

Teacher: Yes, the 100 Chart gives us all the counting numbers up to 100. Does it skip any?

Nicholas: No, but sometimes we do when we count.

Teacher: What happens when we skip count on the 100 Chart?

Linda: We say some and we don't say other ones. And then it makes a pattern.

Teacher: What pattern does it make?

Linda: If we count by twos, we get 5 columns going down.

Ana: All the even numbers. It's a growing pattern.

Frank: I see another pattern. If you look from top to bottom in a line, the second number is always the same, like in 2, 22, 32, 42, 52 and the rest. The other one changes, though.

Teacher: Yes, the ones digit repeats all the way down. But you are right that the other one does change and that makes the number change, doesn't it? 22 is not the same number as 2, even though they end the same.

Jesse: If you go across like 21, 22, 23, 24 and all the way to the end, the last number keeps getting bigger. The first number stays the same all the time, but then it changes at the end. It's 2 but then the last one is 3.

Teacher: Good observation, Jessie. Again, when we look across the row, the first digit repeats until the very last box. The second digit grows by one each time.

Assign the Counting by Tens Homework Master.

Student Guide:
Student Activity Book:
Master: CT
Answers
X
SG_Mini
+
Skip count by two on the 100 Chart
X
+
Skip count by five on the 100 Chart
X
+
Skip count by ten starting at four on the 100 Chart
X
+