Repeating and Growing Patterns
Patterns are a natural object of study for young students. The ideas are accessible and interesting to them. In addition, an ability to recognize, analyze, and extend patterns is a critical element in the development of numeric and algebraic reasoning. This unit focuses on finding and building patterns. Students learn to identify different patterns, to describe them, and to extend them. The activities involve patterns in physical movement, in concrete materials, on the number line, in the 100 Chart, and in drawings of shape and color.
Repeating Patterns
The unit begins by introducing patterns, starting with repeating patterns. A repeating pattern … read more
Repeating Patterns
The unit begins by introducing patterns, starting with repeating patterns. A repeating pattern is one in which the pattern unit is repeated without change. The pattern unit is the group of specific elements that gets repeated. For example:
Pattern Unit: AB
Pattern Unit: ABC
Pattern: ABABABAB
Pattern: ABCABCABC
Students analyze the pattern to isolate and identify
the pattern unit. Using that pattern unit, they add to,
or extend, the pattern. Students also represent the
pattern using the ABC symbolic notation where
each letter represents a specific part of the pattern
unit. We call this notation "alphabet shorthand" in
the lessons. The pictorial pattern 
is
represented in alphabet shorthand as ABCABC
where A represents the square, B represents the circle,
and C represents the diamond. Recording their
patterns in symbols helps students see that one situation
may be represented in different ways and that
different representations can have the same basic
structure.
Growing Patterns
Growing Patterns are patterns in which the basic pattern unit grows or changes in a predictable … read more
Growing Patterns
Growing Patterns are patterns in which the basic pattern unit grows or changes in a predictable way. In other words, in a growing pattern there is an arithmetic change between any two adjacent elements in the pattern. For example, the set of even numbers (0, 2, 4, 6, 8, etc.) is a growing pattern because each element in the pattern is two more than the element preceding it.
In Lesson 5, students describe moves on a number line as a growing pattern. Growing patterns can grow in a positive direction or a negative direction. See Figure 1.
Students are also asked to describe patterns on the 100 Chart in Lesson 7. The 100 Chart is an important tool. The chart is not only a quantitative representation but also communicates the organization of the base-ten number system. It can help students visualize place value and addition and subtraction. These patterns will become easier to recognize and use the more students use the chart to support their thinking.
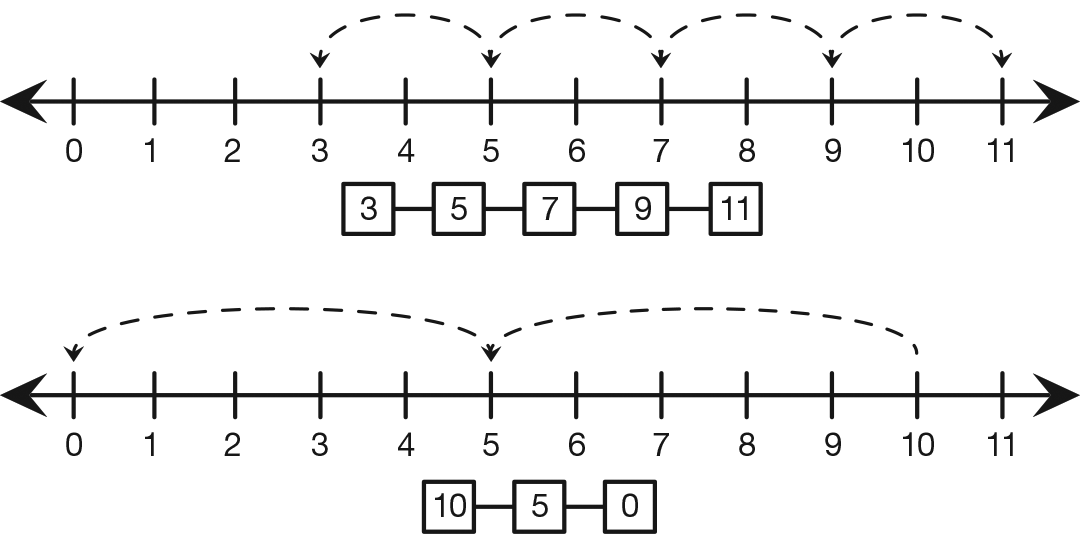
Figure 1: Growing patterns on the number line
Geometric Patterns
In Lesson 8, students compose shapes with pattern blocks along a line of symmetry. The … read more
Geometric Patterns
In Lesson 8, students compose shapes with pattern blocks along a line of symmetry. The context of symmetry gives students yet another way to describe the pattern block shapes.
It is important to note here that a design is not necessarily a pattern in the mathematical sense. Patterns, as we use them here, refer to a specific arrangement of elements as defined above. A design, as we use the term, usually implies an ordered arrangement, pleasing to the eye, but does not necessarily include a repeating or growing pattern. Not every design is a pattern.
MATH FACTS and MENTAL MATH
Addition Facts
Students work on developing number sense and mental math strategies for the addition facts with sums to ten … read more
Addition Facts
Students work on developing number sense and mental math strategies for the addition facts with sums to ten in Groups A and B. See Mathematics in this Unit in Unit 6 for more about addition facts development in Grade 1.
Group A: 0 + 1, 1 + 1, 2 + 1, 3 + 1, 0 + 2, 2 + 2, 3 + 2, 4 + 2
Group B: 3 + 0, 4 + 0, 4 + 1, 5 + 1, 6 + 1, 5 + 2, 6 + 2, 5 + 3, 7 + 1, 1 + 8
These facts involve the counting strategies. For example, what is 1 more than 8 or what is 2 more than 5?
Resources
- Greenes, C.E., M.C. Cavanagh, L. Dacey, C. Findell, and M. Small. Navigating through Algebra in Prekindergarten–Grade 2. National Council of Teachers of Mathematics, Reston, VA, 2001.
- Van de Walle, J.A., K.S. Karp, and J.M. Bay-Williams, Elementary and Middle School Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc., Upper Saddle River, NJ, 2013.