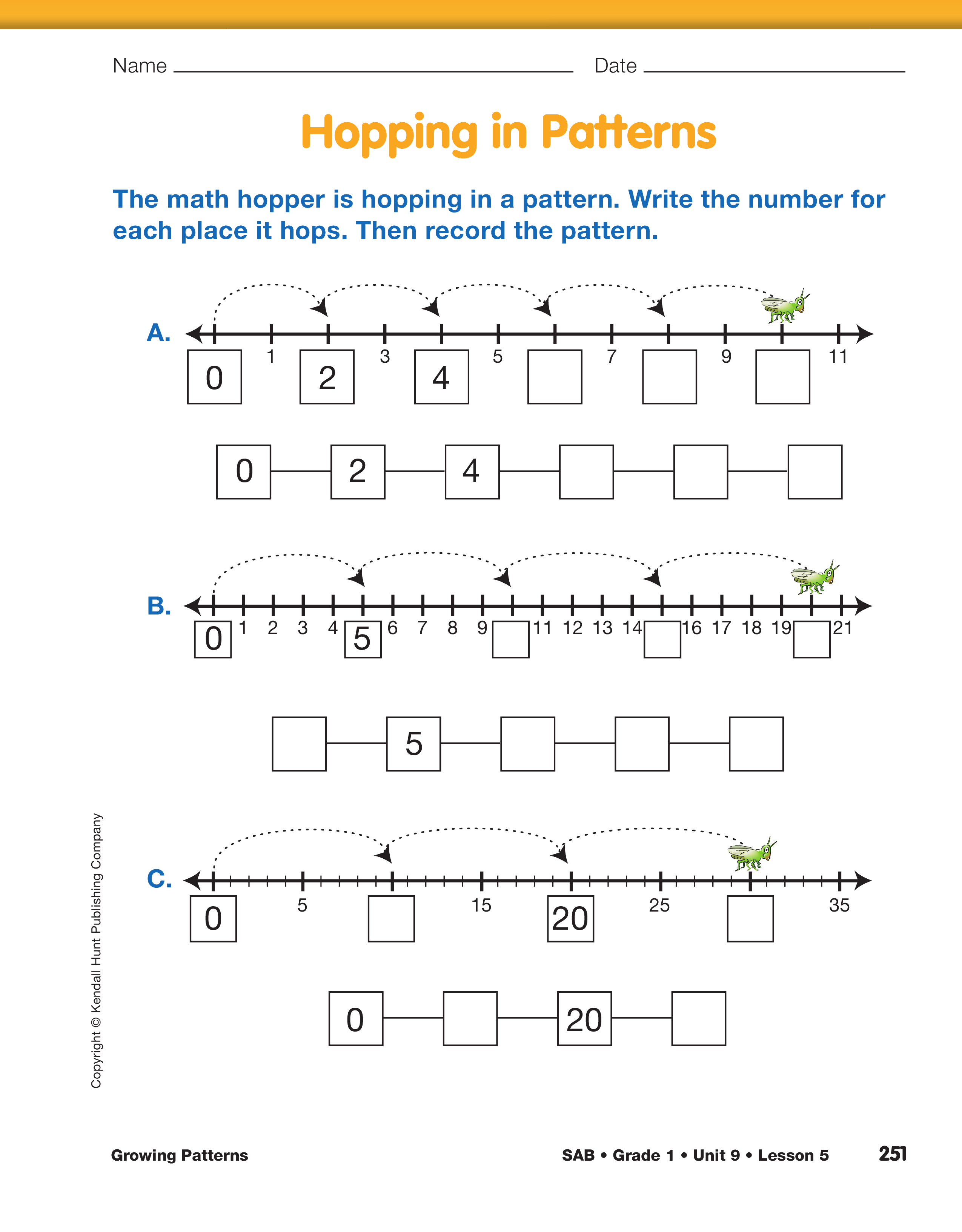
To show growing patterns in which some elements
are missing, display the following: 0, 1, 2, ___, 4, 5,
6, 7, 8.
- What number should go in the empty space? (3)
- How do you know? (Possible response: It's the
next number after 2 and before 4.)
- What is this pattern? (Possible response: It's
counting by ones; add one to the number before.)
- What will be the next number after the 8? (9)
- How do you know? (Possible response: I count on
one more from 8.)
Show a few more examples. Next, display the
Hopping in Patterns pages in the Student Activity
Book. Work on Question A together.
- Look at Question A. The math hopper is hopping
in a pattern on the number line. The numbers in
the boxes are 0, 2, and 4 and then we come to an
empty box. What number goes in the next empty
box on the number line? (6)
- How do you know? (Possible response: Start at 0
and skip every other number.)
- What is this growing pattern? (Possible response:
It's counting by twos starting at zero.)
- Extend the pattern. What other numbers does the
math hopper land on? (8 and 10)
- Now write the numbers in the growing pattern in
the boxes below the number line. (0, 2, 4, 6, 8, 10)
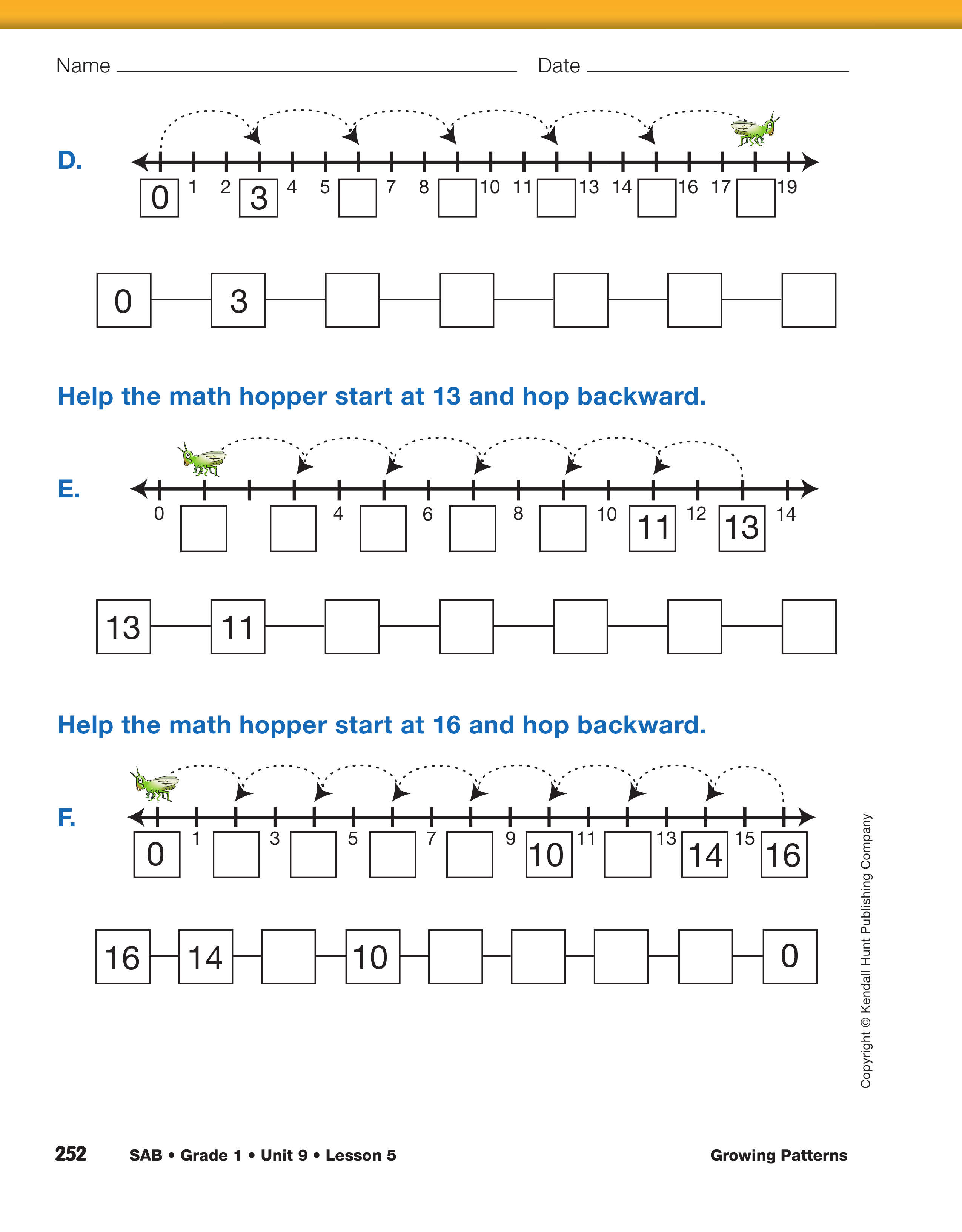
Have students continue to work on Questions B–D.
For Questions E–F, the math hopper is hopping in a
growing pattern that decreases. When students write
the pattern in the boxes below the number line, they
might be surprised to see the highest number in the
first box. Explain that the pattern is decreasing so
they write the highest number first. Work on
Question E together.
- If the math hopper starts at 13 and he's hopping
backward, are the numbers growing larger or
smaller? (They're growing smaller.)
- How do you know? (Possible response: The math
hopper is facing toward the zero so the numbers
are growing smaller; 11 is smaller than 13.)
- We can say that if the math hopper is facing
toward the right, the numbers are getting larger
and if the math hopper is facing toward the left,
the numbers are getting smaller.
- What is the pattern? (Possible response: It's
counting backward by twos.)
- If we start at 11 and go backward, what number
goes in the next box? (9)
- Look at the pattern recorded. Why does 13 go in
the first box? (Possible response: The pattern is
counting backward by twos and we start with
13.)
- When you record the pattern, the first number is
where the math hopper begins and the last number
is where the math hopper ends. Since the
numbers are getting smaller, we start at 13 and
end with 1.
Continue guiding students as they complete
Questions E and F. Remind students that when they
record the pattern the first number is where the math
hopper starts. In Question F the math hopper starts
on 16 and ends on 1, the last number in the pattern.
When students finish the Hopping in Patterns pages,
call on individual students to describe the patterns
they identified and explain their strategies for determining
which numbers to place in the boxes.