Define Line Symmetry. Begin the activity by telling
students they will use a folded piece of paper to make
a shape that is symmetrical using one of the strategies
described in Before the Lesson. Write the word "symmetrical"
on the board and ask students if they have
ever heard the word or if they have ideas of what a
symmetrical picture might look like. When students
finish painting or cutting their images, have them
unfold their papers.
Give them 2 to 3 minutes to discuss
the images with partners.
- What happens when you unfold the paper?
- How would you describe the image? (Possible
response: It looks like the same picture on both
sides.)
- What do you notice about one folded half of the
image compared to the other half?

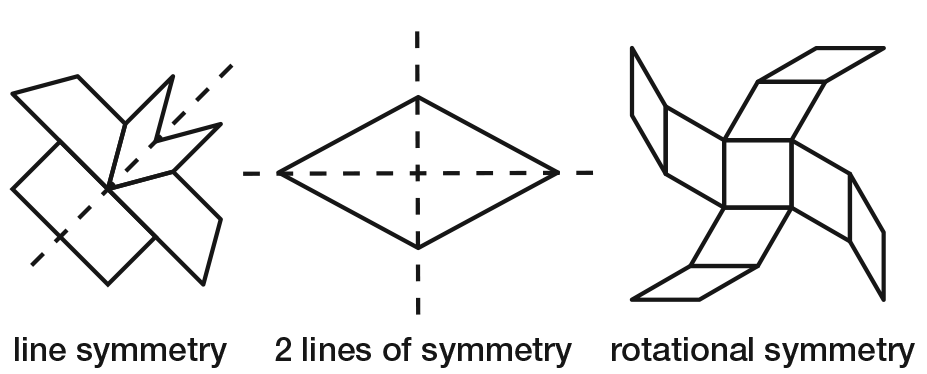
If a figure has line symmetry, it can be folded so that its two
halves match. The fold line is the line of symmetry. It divides
the shape into two congruent halves that are mirror images of
one another. Note that the line of symmetry exists even if it is
not folded or drawn. Folding or drawing helps young children
see where it is. Many figures contain more than one line of
symmetry. For example, a rhombus has two lines of symmetry
as shown in Figure 2.
Another type of symmetry, rotational symmetry, often occurs
in pattern block designs. A figure with rotational symmetry, or
turn symmetry, can be rotated so that it "fits" on itself. The
letter S, for example, does not have line symmetry, but does
have rotational symmetry. It fits on itself if rotated a half turn.
Rotational symmetry will be addressed in second and fourth
grades. However, some students may build designs that have
rotational symmetry. If so, reinforce students who identify it,
and discuss it with the class.
Conduct a class discussion and write comments on
chart paper that relate to the concept of line symmetry.
See the Sample Dialog.
- A figure with line symmetry has two halves.
- The two halves match exactly.
- You can draw a line through the shape that divides
the two sides in half. This line is called the line of
symmetry.
- The figure is flipped from one side over the line of
symmetry to the other; it is a mirror image.
- Sometimes the line of symmetry is there, but many
times it is invisible. Drawing it helps us see where
it is.

Use the Sample Dialog to guide a discussion of symmetry.
Teacher: Remember, I told you that we would make
pictures that could help us learn what symmetrical
means. What did you notice about your picture,
Keenya?
Keenya: I only painted one and it made two. And they are just
the same.
Teacher: That's interesting. How did it make two?
Keenya: I painted on this side. Then it smeared onto the
other side when I folded it.
Teacher: That's right, but why are they the same? [Writes
"same picture" on the board under the word
"symmetrical."]
Keenya: Because it painted on the other side only in the places
where there was already paint.
Teacher: Yes, because the paint on one side made its
same picture onto the other side when you folded it.
Anyone else have a comment?
Michael: Mine is backward. This one on my first side has a
stick coming out, and the other picture has a stick
coming out, but it's on the other side of it.
Teacher: That's an interesting thing to notice, Michael. The
second picture is not just exactly like the first one, is
it? Something is different.
Michael: It is just the same, except it's turned over.
Teacher: Yes, we say it looks like someone flipped it over.
The exact same picture, just flipped over. [Writes
"flipped" on the board.] Anything else?
Jessie: On mine, it's like there's a line down the middle.
Anything that's on one side is on the other side of the
line.
Teacher: That's another good point, Jessie, and we'll write
that on the board, also. It's like there is an imaginary
line down the middle of the picture. It divides the
paper into two sides. We call this the line of
symmetry. Everything on one side of it is exactly like
everything on the other side, except it's flipped over.
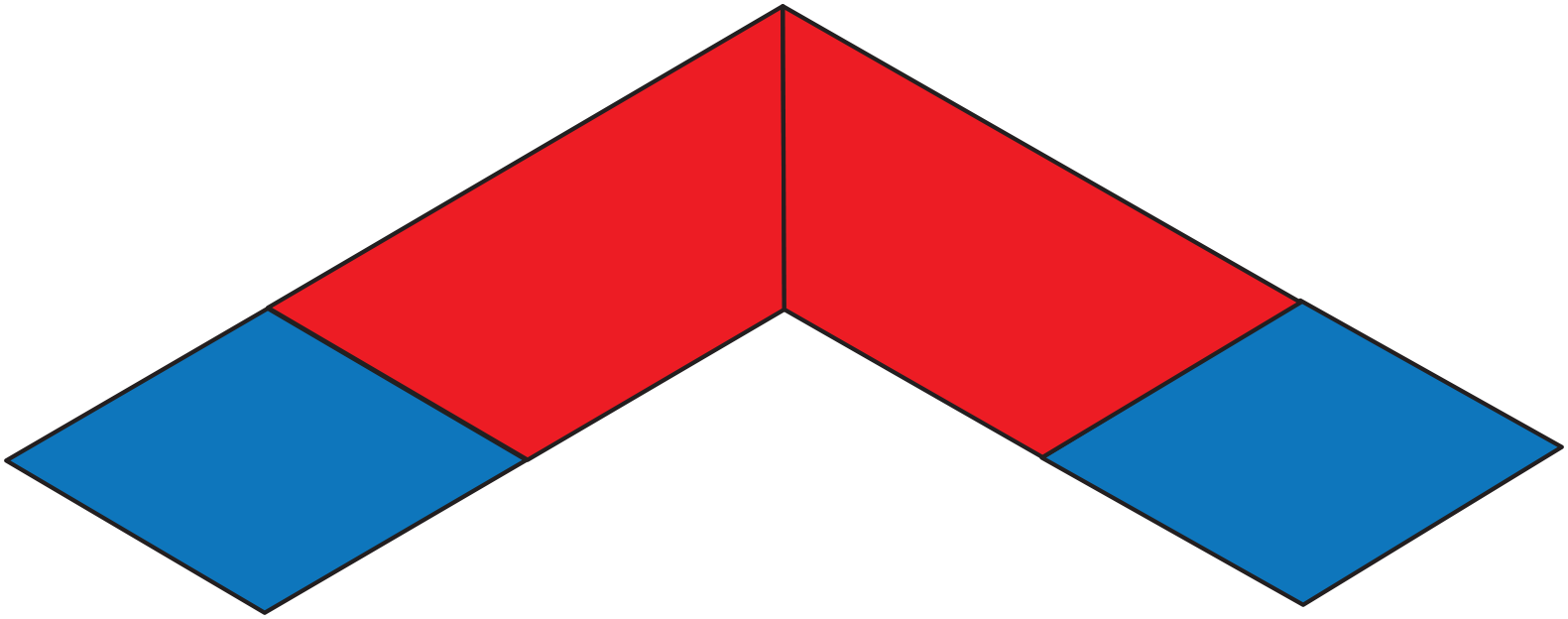
Make Symmetrical Shapes.
Introduce symmetrical
shapes by displaying the pattern block design in
Figure 3.
- Is this shape symmetrical? If you cut it in half would
each half be the same? (Yes.)
- How do you know? (Possible responses: one side is
just like the other side; I could flip one half on top
of the other half.)
- Where would you cut the shape in half? (Between
the trapezoids)
Direct students' attention to the Pattern Block
Symmetry pages in the Student Activity Book. Display
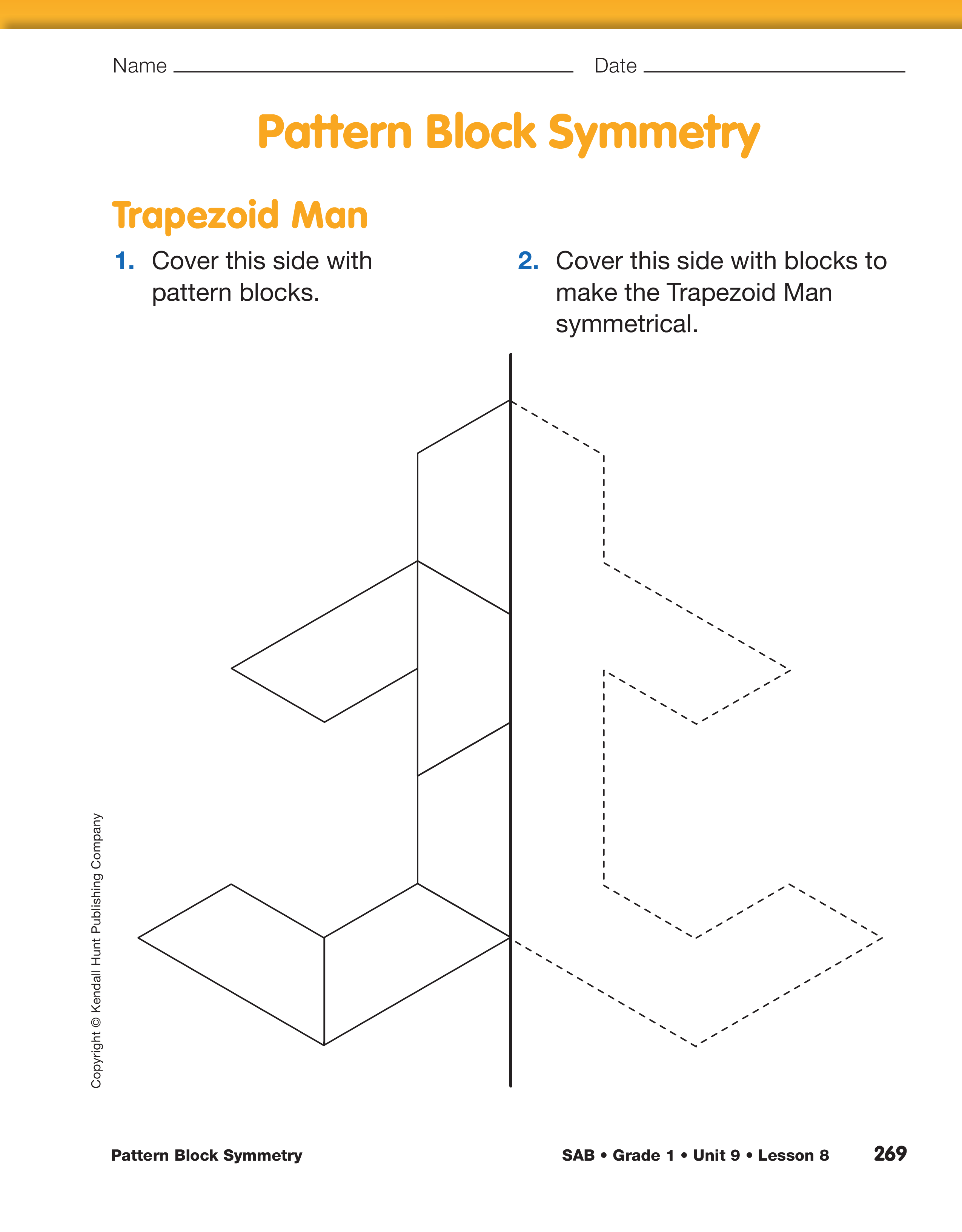
the Trapezoid Man shape and Questions 1–2. Ask students
whether they think the shape is symmetrical.
Elicit an observation that the figure is symmetrical
except for the fact that the left-hand side is drawn
with solid lines, the right-hand side with dotted lines.
Ask students to fill in the left-hand side with solid
lines using pattern block trapezoids. Then place one
or two pattern blocks on the right-hand side.
- How can I find out where I should place the pattern
block on the other side to make Trapezoid Man symmetrical?
(Possible responses: The blocks will be
the same but flipped. I can cover the blocks on the
first side then flip the blocks over the line. Or, I
can flip the blocks on the first side over the line
and then fill in the first side again).
Ask students to use trapezoid pattern blocks to cover
both sides of the Trapezoid Man page. Emphasize that
students should put the pattern blocks on the half with
solid lines first. When students have covered the
shape with blocks, ask a volunteer to complete the
page using a set of pattern blocks on a display.
- How did you decide where to put the blocks?
- Is Trapezoid Man symmetrical? How do you know?
(Possible responses: He is the same on both sides,
only flipped. If I folded him in half, both sides
would match.)
- Show us the line of symmetry.
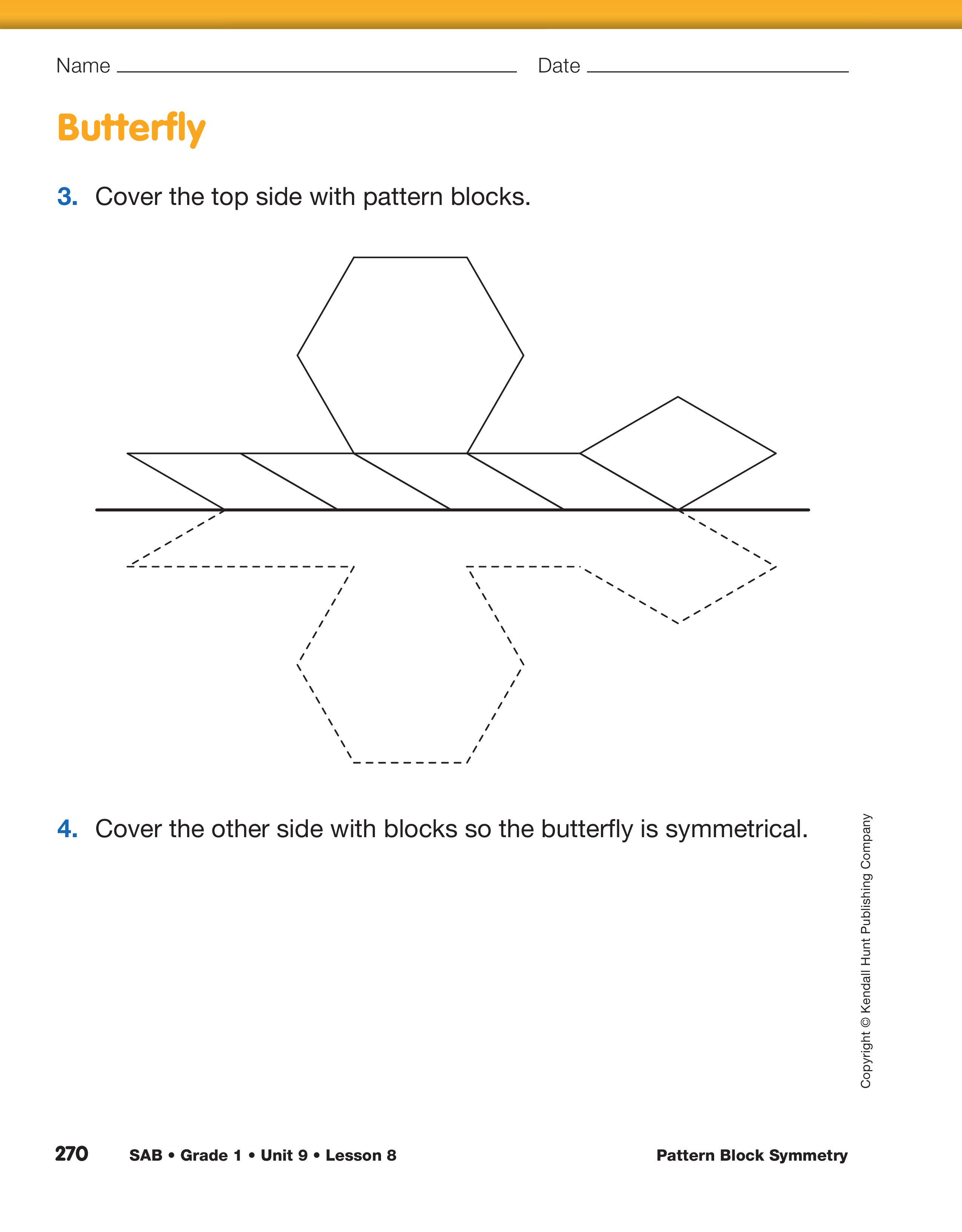
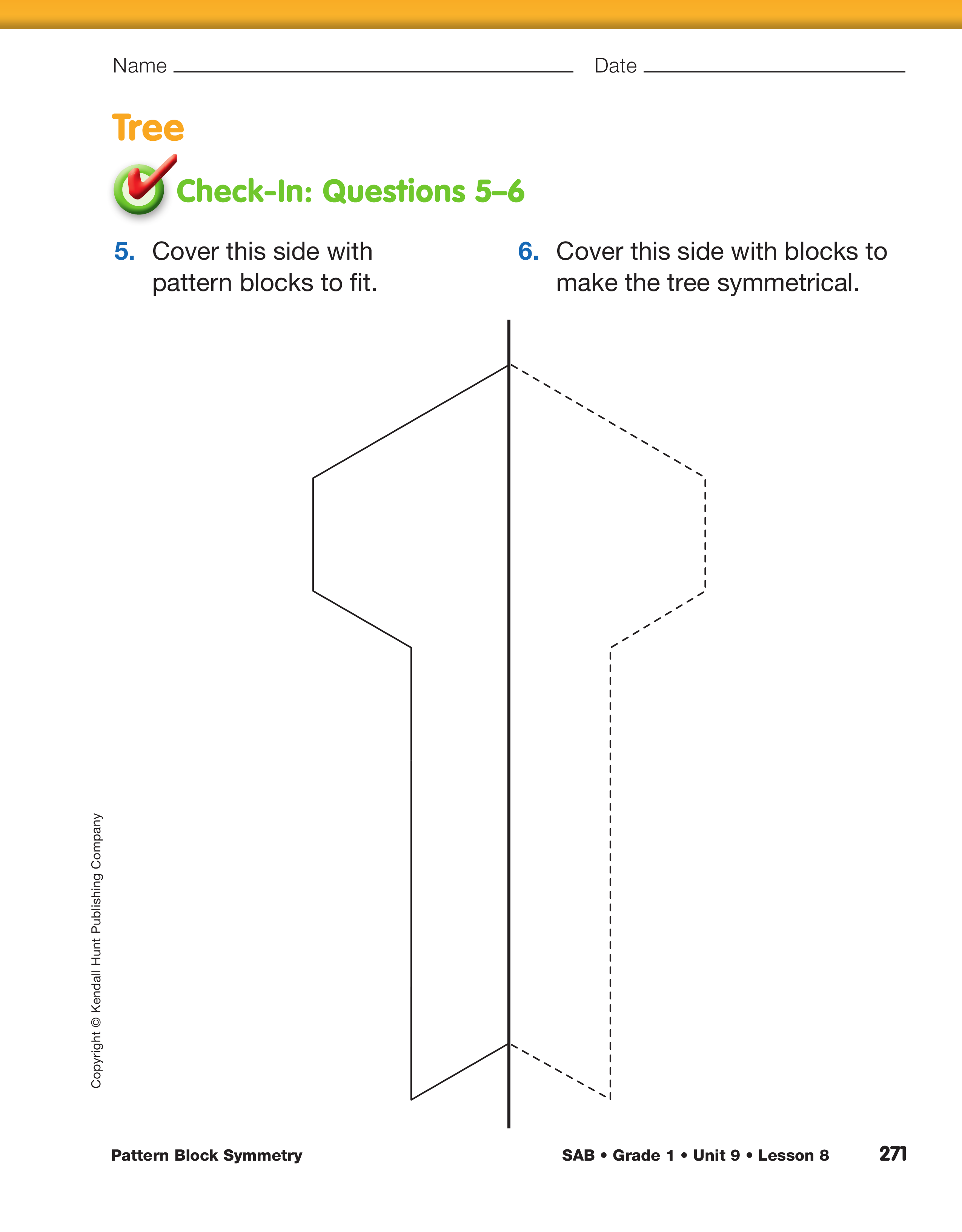
Ask students to continue with Questions 3–6 to cover
the Butterfly and Tree shapes using various pattern
blocks as needed.
If students work in pairs and use one page from each Student
Activity Book, they can display their work on both the
Trapezoid Man and Butterfly sections at the same time.
Use Check-In: Questions 5–6 on the Pattern Block Symmetry
pages in the Student Activity Book to assess students' abilities
to use pattern blocks to compose a figure so that it is
symmetrical. [E7].
The Is It Symmetrical game described in this lesson can be
used as targeted practice composing shapes with line
symmetry [E7]. Place copies of the page from the Student
Activity Book and some pattern blocks in a learning center.
Is It Symmetrical Game.
Introduce the Is It
Symmetrical game by asking a student volunteer to
play it with you on the display. Draw a vertical line to
represent the line of symmetry, or use a display of the
Is It Symmetrical page from the Student Activity Book.
The game is played in pairs. The first player begins by
placing one pattern block on the right side of the line.
The second player places two pattern blocks on the
left side of the line, one that is symmetrical to the first
player's block and another for the first player to do
the same in the next turn. Pairs continue to play until
there are 12 to 14 blocks on the page. Have students
play the game in pairs.
In a variation of this game, players can place two or
three pattern blocks at a time on one side for the other
player to add to on the other side to make a symmetrical
figure.
After playing several rounds of the game,
ask:
- What was difficult or easy about the game?
- What strategies did you use? (Possible response: I
looked at the piece on the board and then took
another piece just like it and flipped it across the
line of symmetry).
Introduce the My Pattern Block Shape page by
explaining to students that they are to construct their
own symmetrical shapes with six pattern blocks.
- How will you choose which pattern blocks to use
and how many?
- What strategy will you use to complete the pattern?
Walk around the room and note whether the pattern blocks have been placed in a symmetrical shape and
whether the students use a strategy that includes flipping
the blocks over the line of symmetry.
Take photographs of students' shapes to collect and share
symmetrical pattern block shapes.
Use the My Pattern Block Shape page in the Student Activity
Book to assess students' abilities to compose a simple
symmetrical shape. [E7].