Define Fair and Equal Shares.
Begin instruction
by asking:
- What does it mean to share something fairly? (Everyone has to have exactly the same amount.)
- Can you give an example of fair shares? Use connecting
cubes if it will help you explain. (Possible
response: If I had some gumballs and I gave
everyone 5 of them, I shared them fairly because
everyone has the same number of gumballs. No
one has more than 5 and no one has less than 5.)
- Would it be fair shares if I had 10 pieces of candy
and I gave one child 8 pieces and another child
2 pieces? Why or why not? (No, because everyone
has to have the same amount when you share
something fairly.)
- If I gave one child 5 pieces of candy, and the other
child 5 pieces, then have I shared the candy fairly?
Are the groups equal? How do you know? (Yes; If
the groups are equal, that means they have the
same amount so they have been shared fairly.)
- Does equal shares mean the same thing as fair
shares? Why do you think so? (Yes, I think they
mean the same thing because if you share something
fairly each group will have equal shares.)
Solve Fair Share Problems.
Present students with
the following problem:
- Four children want to share 10 oranges so that
everyone gets exactly the same amount. They
want to share all of the oranges. How much orange
can each child have?
Allow students to find a solution with a partner.
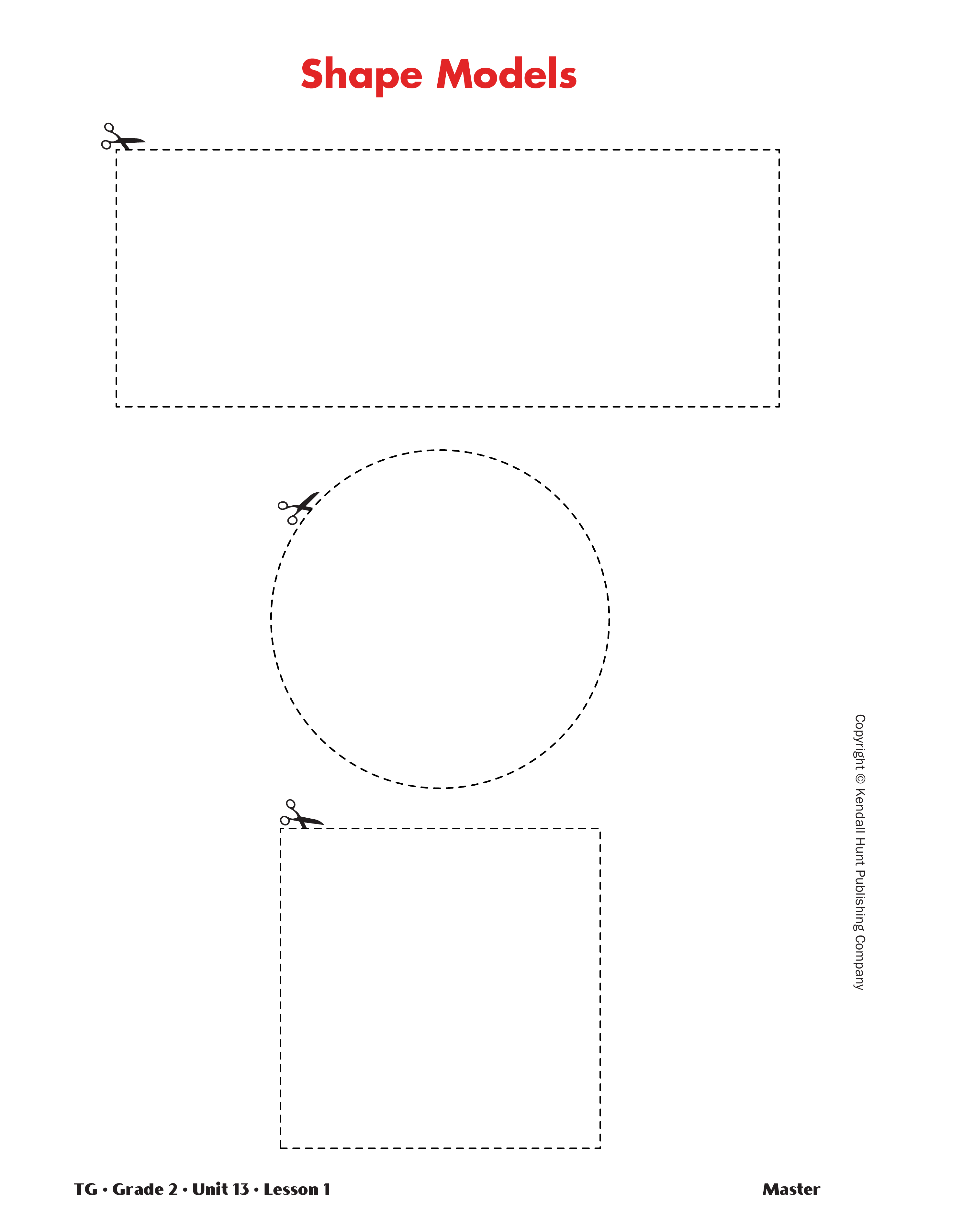
Provide access to copies of the Shape Models
Master, paper, crayons or colored pencils, scissors,
and connecting cubes. Circulate as students work.
Two common mistakes students make when solving
fair share problems are not sharing all of the items
and not creating equal groups.
To help them work
through the problem, ask questions such as:
- They want to share these oranges too. How can
they do that?
- Does every child have the same amount of
orange? How do you know?
This problem allows students to combine what they
know about whole numbers and division and apply it
to partitioning into parts. Students do not need to be
able to read or write fractions to be able to solve the
problem. See Content Note and Figures 1 and 2. The
problem's meaningful context, equal sharing, is
familiar to students. Most children have experience
with fairly sharing food, toys, crayons, and so on,
and can informally apply their prior knowledge of
partitioning in the solution process.

Communicating Solution Strategies. Students do not need
to use fraction terms or symbols to explain the number of
items or parts in a fair share. It is likely that some students
may begin this unit of study using terms like "half" or
"fourth" accurately, but other ways of describing the amount
or part of a share are appropriate at this level, too.
See Figure 1.
Students often understand the concepts behind equal sharing
problems and partitioning situations before they are
physically able to accurately create models that represent
equal partitions. It is developmentally appropriate for
students to verbally express their understanding that, for
example, each of the three parts needs to be equal and to use
their own models and representations even if they are not
exactly accurate. See Figure 2.
The problem involves mixed numbers. Because of
their previous understanding of sharing, students
can make sense of what to do with the remaining
two oranges after the other oranges are distributed.
Students often do not realize that fractions are a type
of number. When they solve problems such as this
one involving a set of objects that they can count and
also split into parts, students learn that fractions are
numbers that come between whole numbers. They
can be found on a number line. It also helps students
see that fractions are not just numbers between 0 and
1, another common misconception.
After students have had time to solve the problem,
discuss solution strategies. Equal sharing problems
such as this one involve items that are easily drawn
and divided so many students will likely draw pictures.
See Figure 3.
- How many children are sharing in this problem? (4)
- How many oranges are being shared? (10)
- Does each child get more or less than 1 whole
orange? (more than 1 whole orange)
- Is that reasonable? (Yes, because there were a lot
more oranges than children.)
- How many whole oranges does each child get? (2 whole oranges)
- Were there any more oranges to share? (yes,
2 more)
- How did you fairly share the 2 extra oranges? (Each child got another part of one whole:
one-half.)
- Were all of the oranges shared when you were
done solving the problem? (yes)
- How did you find out how many oranges each
child would get? Did any tools help you see or
model the situation in the problem? How? (Possible responses: a drawing, connecting
cubes, pieces of paper to represent the oranges)
- How do you know that you shared all the oranges
fairly? (Possible response: When I was done, I
made sure that each child got the same amount.
No one got more orange than another person and
all of the oranges were shared.)
- Did anyone solve this problem a different way?
Show us.
- [Student name], I heard you call the small parts
"halves." What does a half mean to you? (Possible
responses: Half means two equal pieces or parts;
my mom cut my sandwich into 2 same-size
pieces or halves; there are two half hours in an
hour; you can give a half dozen cookies to one
person and a half dozen cookies to another person.)
[See Content Note.]
- What is important to remember about halves? (Halves are two equal parts of a whole.)
- How many halves are in one whole orange? (2 halves)

Common Misconceptions. When students use fraction terms
such as half, third, or fourth, it is necessary for them to use
the terms accurately. Many children think any division into
two parts is a division into halves. This is revealed by
statements such as "I want the bigger half." Some students
think any piece of a whole unit is a "half." For example, "I cut
the pizza into four pieces so everyone could get a half."
Another common misconception is to associate the number
in a set with the fraction name. For example, a student fairly
sharing 12 marbles among 4 might call the group of marbles
"thirds" because there are 3 marbles in each equal group. As
students' understanding grows, they will learn that a
fraction's name depends on the size of the part in relation to
the unit whole. Help students by defining the terms in
relation to equal sharing. An object or objects shared equally
by 2 will result in 2 equal halves. An object or objects shared
equally by 3 will result in 3 equal thirds, and so on.
Direct students' attention to Questions 1–2 on the
Share Fairly pages in the Student Activity Book. Ask
students to work with a partner to solve the problems.
Students are asked to divide objects equally
among 2 or 4 children. Monitor students as they
work so that you can select volunteers with a variety
of solution strategies.
When students have completed Questions 1–2, ask
volunteers to explain their solution strategies.
- How many children are sharing in this problem?
- How many [cupcakes, cookies] are being shared?
- Were all the [cupcakes, cookies] shared?
- Does each child get more or less than 1 whole
[cupcake, cookie]?
- Did anyone use models? How was it helpful to use
[a drawing, connecting cubes, etc.]?
- How did you know that the items were shared
fairly or equally?
- Did anyone solve this problem a different way?
Correct Common Mistakes. Next, ask students to
complete Questions 3–4 on the Share Fairly pages.
They will critique other students' work and correct
mistakes commonly made when sharing fairly. In
Question 3, Julia shares all the bananas but does not
create equal groups. In Question 4, Mark creates
equal shares, but does not share all of the brownies.
He has one left that can be further divided among
4 friends.
Upon completion, use a display of the Share Fairly
pages to facilitate discussion about how students can
help Julia and Mark share fairly.
- What one important thing does Julia need to
remember when sharing equally? (All the groups
need to have the same amount of items in them.)
- How can Julia share the bananas fairly? (She
needs to give everyone 2 bananas and then
one-half more.)
- What one piece of advice about fair shares would
you give to Mark? (He needs to share all of the
things and not have any left over. He could break
the leftover brownie into parts so that he can
share all the items.)
- How can Mark share the remaining brownie fairly
among 4 friends? (He can cut it into 4 equal
pieces.)
- If he cuts the remaining brownie up and shares it,
do all the pieces need to be the same size? (yes)
- I heard [student name] call each of the small
brownie pieces a "fourth." Is that a good name for
each of the four equal parts of the brownie? Why
or why not? (Possible response: Yes, because it is
easy to remember that if you cut something into
four equal parts, each part is one-fourth. Also,
there are 4 people sharing the brownie, so each
fair share is one-fourth.)
Use Words and Models to Describe Equal Shares. Assign student pairs Questions 1–6 on the Equal
Shares pages in the Student Activity Book. Students
will divide objects into equal shares of 2, 3, and 4.
- How is the sharing problem in Question 1 different
from the sharing problem in Question 2? (In
Question 1, I divided up all the pickles and there
was one left that I had to split into two parts. In
Question 2, there were no leftover cars to divide
up. Everyone got 9 cars.)
- Were you able to share all of the pickles and all of
the cars fairly? How do you know? (I know I
shared fairly because each of the children got
7 and one-half pickles and there were no pickles
left to share. All 18 of the cars were shared and
each child got 9.)
- What did you notice about Question 3? Were you
able to share all of the cars fairly? (No; each child
got 4 cars and there were 2 left over but I
couldn't cut the cars apart to share them.)
- Did anyone use a model to decide how to share
7 ice cream sandwiches among 3 girls in
Question 4? Show us how you used a model. (Possible response: I gave each girl 2 ice cream
sandwiches, but I still had one to share. I cut out
the rectangle on the Shape Models Master that
looked like an ice cream sandwich, cut it into
3 equal pieces, and gave each girl one of those
small pieces.)

Allow students to use any model that makes sense to them. If
a student struggles with the fair share problems, encourage
him or her to use connecting cubes or slips of paper to
represent each item to be shared (oranges, cupcakes,
brownies, etc.) They can use one small container to
represent each child sharing the items. Students can count
out the cubes or slips of paper and distribute them one by
one to each container. When the numbers are odd, students
can imagine cutting the cubes into smaller equal parts, or
they can actually cut the slips of paper into equal parts so
that all of the items can be fairly distributed.
Distribute one small rectangular self-adhesive note
or an index card to each student. Ask them to use the
note or card to make a model of the last leftover ice
cream sandwich. Have students share ways to divide
the rectangle into three equal shares. Help students
recognize that there are different ways to partition
the rectangle into thirds and that equal shares of the
same whole do not have to be the same shape.
Students use halving to partition a shape into two
equal parts. They find a half of a half to find fourths.
Partitioning a shape into thirds is more difficult. At
this stage, do not be concerned with students' abilities
to perfectly divide the rectangular model into
thirds. Instead focus on their discussion and understanding
that the parts are equal in size.
- When you fairly shared something with 2 people,
you called each equal part a half. When you fairly
shared something with 4 people, you called each
equal part a fourth. Can you think of a name for
each of the three small ice cream sandwich
pieces? (a third)
- Why is a third a good name for each of the small
pieces? (You have to share one whole ice cream
sandwich among 3 people, so you have to make
3 equal shares. Each equal part of the ice cream
sandwich is one-third.)
- Why is it important to share the leftover parts (the
thirds) equally, too? (Possible response: In order
to share fairly, everyone has to have the same
amount. So they have to get the same amount of
whole items and the same amount of parts.)
- Do all the leftover parts or thirds need to be the
same size, or can some be bigger than the others? (The thirds need to be equal in size.)
Discuss Questions 5–6 on the Equal Shares pages.
Question 5 presents another situation to help students
recognize that equal shares of the same whole
do not have to be the same shape.
- In Question 5, what did you notice about the different
ways Carla and Kim divided the sheet of stickers?
Were they fair? (They cut up the sticker
sheet into different shapes, but each girl still got
3 stickers, so I think it is fair.)
- How did you share 11 pizzas with 4 boys for
Question 6? Did anyone use a model? Show us. (Possible response: I knew there was enough for
everyone to get 2 pizzas. Then there were still
3 pizzas left. I gave everyone another half and
there was still 1 whole pizza left. So I cut the last
pizza into fourths and gave each boy another
fourth. Each boy got 2 whole pizzas, a half, and a
fourth.)
- Is there a name for each of the four small parts of
the whole pizza? (Each piece is a fourth.)
- How do you know that you shared the pizza fairly? (All the pizza has been shared and each boy has
the same amount: 2 whole pizzas, a half, and a
fourth.)
Assign Check-In: Questions 7–9 on the Equal
Shares pages for students to complete individually.
Use Check-In: Questions 7–9 and the Feedback Box on the
Equal Shares pages in the Student Activity Book to assess
students' abilities to partition shapes and sets into equal
shares [E2]; find a strategy [MPE2]; and communicate
solution strategies [MPE5].