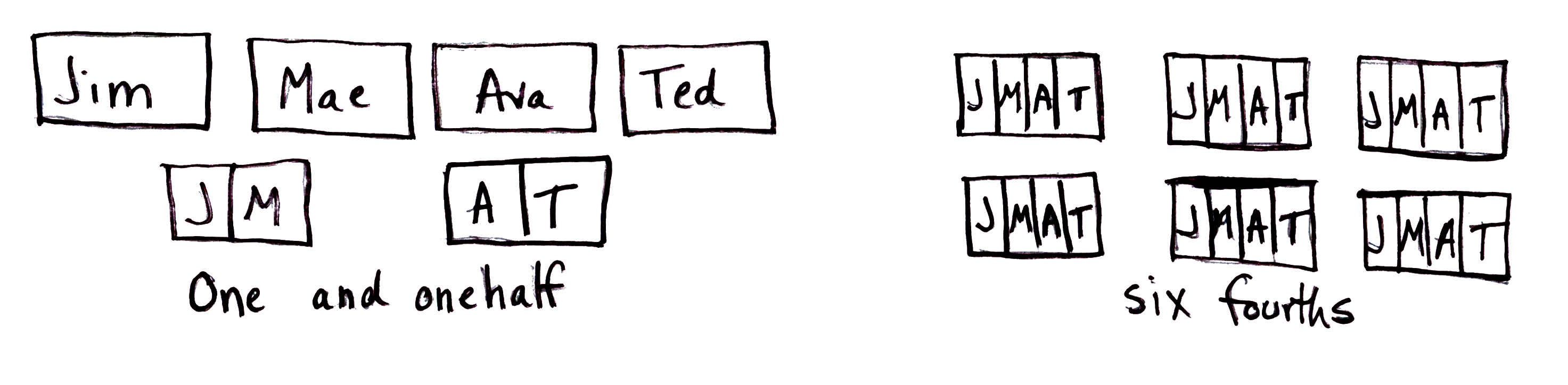Lesson 1

Equal Shares

Est. Class Sessions: 2

Summarizing the Lesson

To summarize the lesson, display the Sharing Sandwiches Master. Cover the bottom half of the Master so that the top half only is displayed.

Say:

X
  • I want to share these 3 submarine sandwiches equally between my friend and me. Show how I can do this.

Ask a student volunteer to demonstrate how to share the sandwiches fairly between two. Then uncover the bottom half of the Master, revealing the way that you decided to share the sandwiches.

Ask:

X
  • I took one and one-half sandwich and I gave my friend one and one-half sandwich. My friend said, "I want the bigger half." What do you think about that? (Halves are two equal parts of a whole. There can't be a bigger half.)

Draw students' attention to the last part of the Master that shows an alternative way to partition the sandwiches.

Ask:

X
  • My friend thought it might be fairer to share the sandwiches this way. He used "Y" to mean yours and "M" to mean mine. What do you think about my friend's solution? (Both ways of sharing the sandwich are fair.)

Partitioning each whole into halves is not an uncommon approach to fair shares and will arrive at a correct solution. Although it may take more time, for example, to partition each of 6 sandwiches into fourths to find 4 fair shares of 6, it is an acceptable solution strategy. Equal shares of the sandwich do not have to be the same shape. See Figure 4. Students will eventually learn that they do not need to partition every single item to figure out how much of each is in each share and will move toward more efficient strategies.

Adventure Book:
Student Activity Book:
X
SG_Mini
+
X
SG_Mini
+
Master:
Two ways to solve 4 friends share 6 sandwiches
X
+