Find Area

Est. Class Sessions: 2

Developing the Lesson

Part 1: Choosing Appropriate Units of Measure

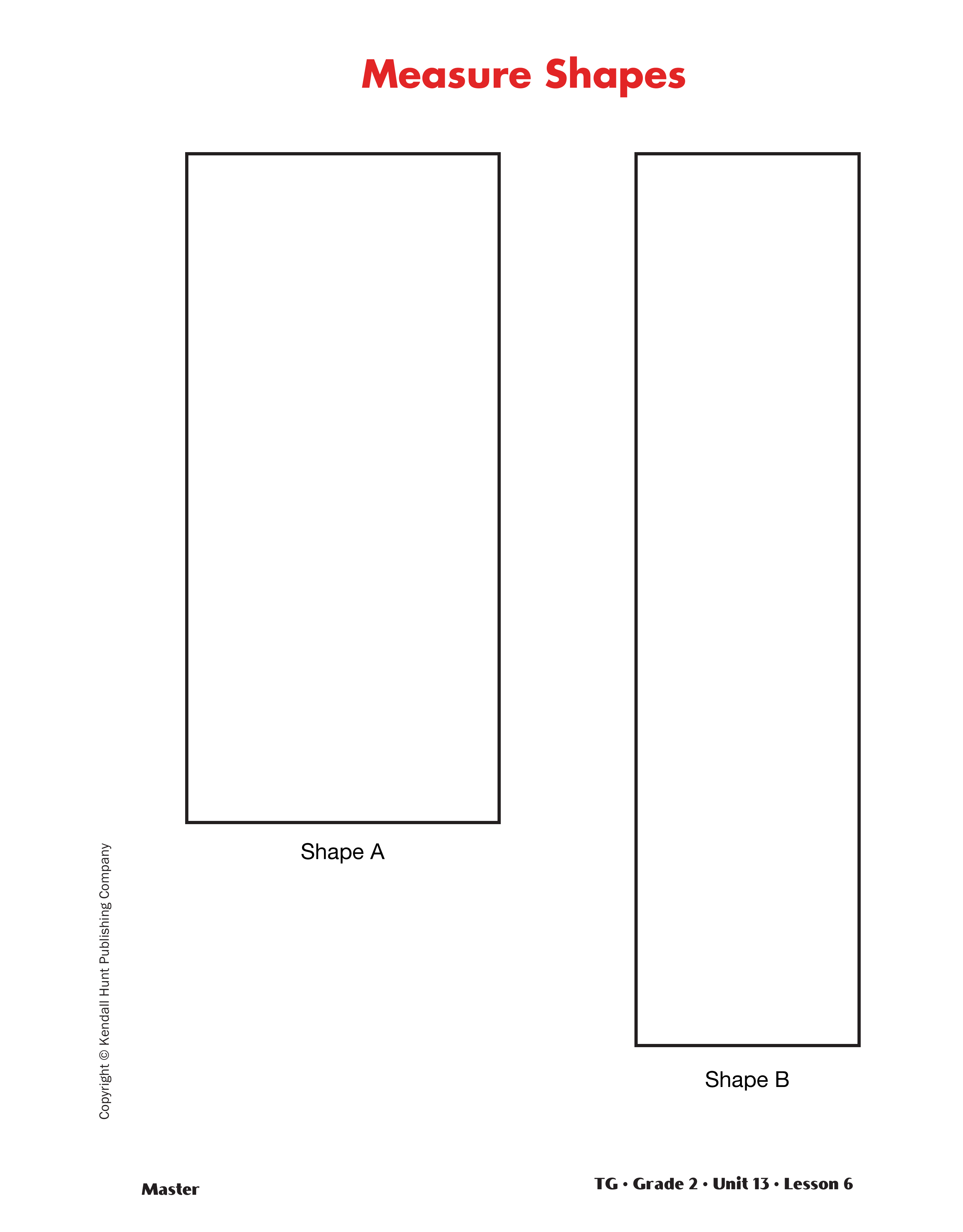
Measure Area. Display the Measure Shapes Measure Shapes Master that shows the outlines of two rectangles, Shape A and Shape B.

Ask:

How can we compare the sizes of these two shapes?

Some students will probably mention using a ruler to measure the sides, or even the diagonals of the rectangles and using these measurements for comparison. Validate the idea of using length to measure the size of the objects. Shape B is longer than Shape A. Shape A is wider than Shape B.

Explain that another way to compare the size of the rectangles is to compare the area inside the shapes. Define area for the students as the amount of space each rectangle covers. Distinguish area measurement from measuring the length of the sides which are simply lines.

Allow time for the students to consider how they can solve this problem. Guide them to the idea that the shapes can be covered with something that will give them a basis for comparison.

Ask:

What are some units we can use to cover the shapes? (Possible response: tiles, squares)
How can we measure and compare? (count them)
Can you think of ways to measure that would not give an accurate measurement? (Possible response: If all the units were different.)
What other important things do we need to think about when covering these shapes?

The goal of the discussion is to bring out the following four measurement concepts:

Everyone must agree to use a single unit within a shape.
Everyone must agree to use the same unit in each different shape.
The size of the unit should be uniform (the same each time we use it).
The units should cover the entire area without gaps.

Use a Single Unit. To demonstrate the first concept, fill in the area of the shape with an assortment of objects, such as erasers, coins, pencils, chalk, and paper clips. See Figure 1.

Ask:

What problems do you see with measuring this way? (All the units are different sizes and shapes.)
How can I report a measurement using all these different objects at the same time? (You can't.)

Use the Same Unit. To demonstrate the second concept, cover Shape A using one unit, such as paper clips, and Shape B using a different and larger unit, such as chalk. See Figure 2.

Ask:

If I measure the two shapes with these two units, can I tell which shape is larger? (It's hard to compare because they are different units.)
It seems like Shape A is larger because it takes more units to cover. Is this right? (no)

Use Uniform-Size Unit. To demonstrate the third concept, cover one shape with two sizes of paper clips (large and small). See Figure 3.

Ask:

Is this a good way to measure? Why or why not? (Possible response: No, because some of the paper clips are small and some are big.)

Cover the Area without Gaps. To demonstrate the fourth concept, cover one shape with pennies, leaving gaps between them.

Ask:

What is the problem with covering an area like this? (There's too much space between the pennies.)
Is this kind of measurement accurate? Why or why not? (No, because you can't count the space.)

Using round objects, such as pennies, can provide a good estimate of the area. Although the area will not be exact, it is still possible to compare the area of both rectangles using pennies for measurement. However, we want the students to conclude that we can get a better estimate of the full area if we place the units compactly, leaving as few gaps as possible.

Ask:

How can we get a better estimate? (Rearrange the pennies so that they are closer together.) [See Figure 4]

Some students might suggest covering the shape with square tiles. If it is suggested cover each shape with tiles and ask a student to demonstrate how to find the area of each shape.

You might also ask:

When you cover the shape with square-inch tiles, they hang over the edge of the shape. What do you think you can do about this?
How many square-centimeter tiles cover this shape?

Adventure Book:

Student Activity Book: