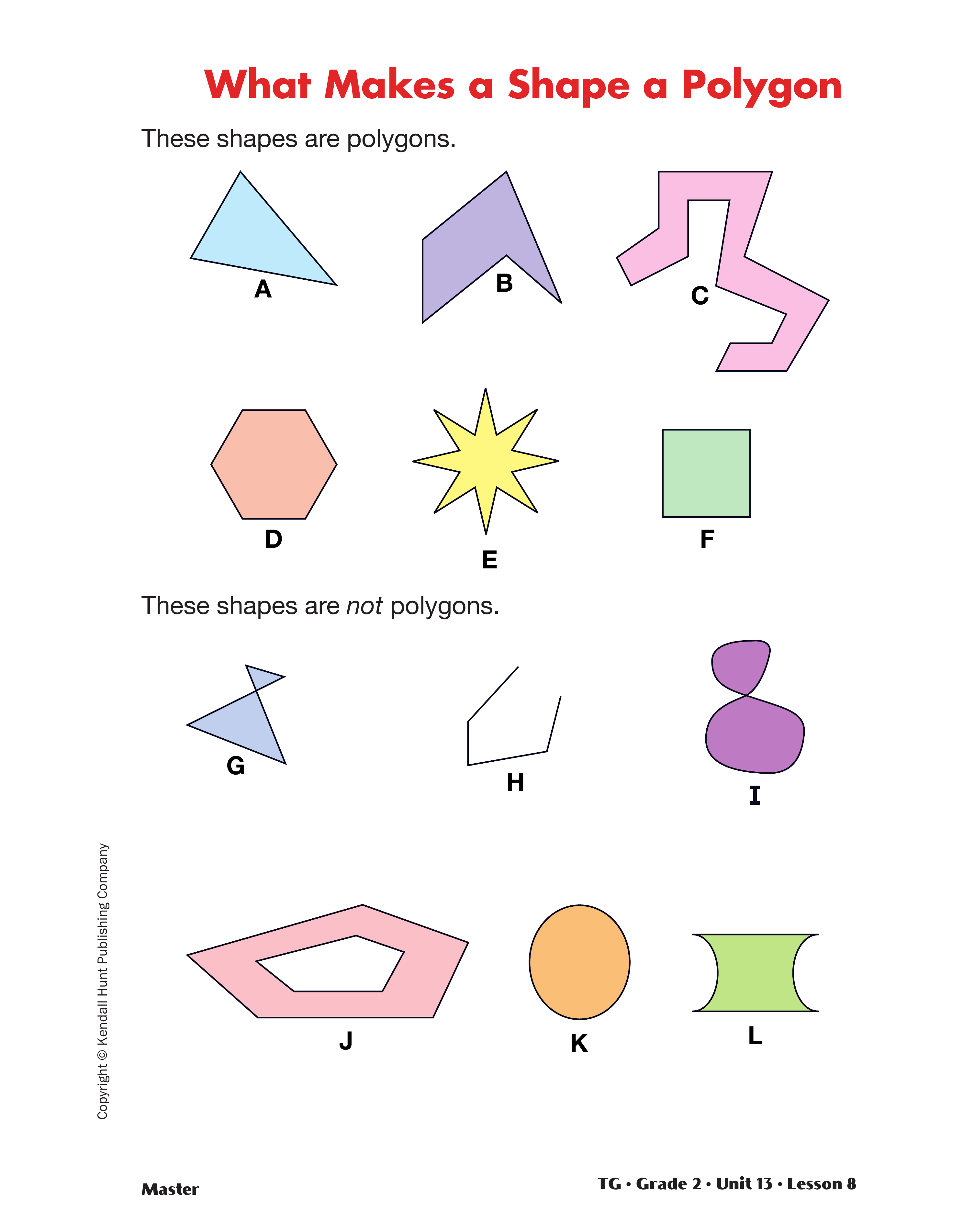
Introduce Polygons. Use the display of the What Makes a Shape a Polygon Master in the Teacher
Guide to introduce polygons. Ask students to look at
the differences between the shapes that are polygons
and the shapes that are not polygons.
- What is a polygon? (Possible responses: Polygons
have straight sides. They are closed shapes. They
have corners or angles.)
- Why is Shape H not a polygon? (The shape is not
closed.)
- Why is Shape K not a polygon? (The shape has
curved sides.)
- Why is Shape J not a polygon? (The shape has a
hole in the middle.)
- What about Shapes G and I? (The shapes have
two parts or are concave and the sides cross each
other.)
- What about Shape L? (Two sides are straight but
two sides are curved.)
Geometric Vocabulary. Let students use their own words
when describing the shapes or polygons. As they arise
naturally in context, use the precise geometric terms
synonymously with less formal language. For example,
when discussing the differences between the square and the
blue rhombus, you can use the terms angles and corners
interchangeably.
Tell students that in this lesson they are going to
focus on closed shapes that have straight sides and
angles. Students may choose to identify these shapes.
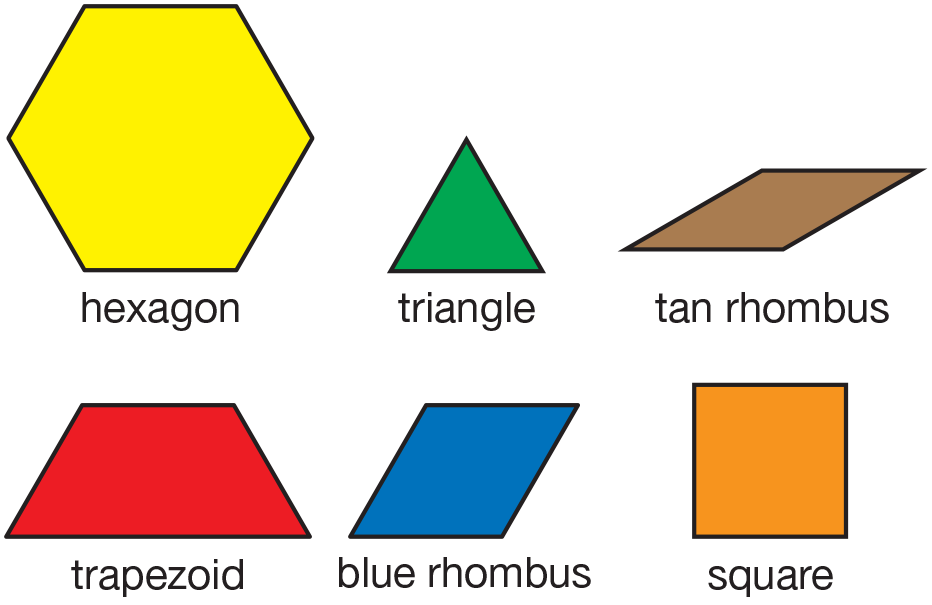
Identify Pattern Block Shapes. Students will not
need a complete set of pattern blocks for this lesson.
They will only need a hexagon, green triangle,
tan rhombus, trapezoid, blue rhombus, and a square.
Say the name of each shape and ask students to find
it in their set and hold it up. See Figure 1. Store the
remaining pattern blocks in a resealable bag and set
them to the side.
Compare Number of Sides and Angles.
To help
students compare the number of sides and angles of
the shapes in their small set of pattern blocks, ask:
- Find the shape that has 3 sides. What is it called? (triangle)
- Find the square. How is the square different from
the triangle? (Possible response: The square has
four sides but the triangle only has three.)
- How many corners does the triangle have? (3) The
square? (4)
- What is another name for a corner? (angle) [See
Content Note.]
- Which shape has the most angles? How many
angles? (The hexagon has 6 angles.)
- How many sides does the hexagon have? (6 sides)
- How many sides and angles do the rhombuses
have? (4)
- In these pattern block shapes, how are the number
of sides and number of angles related? (They are always the same.)
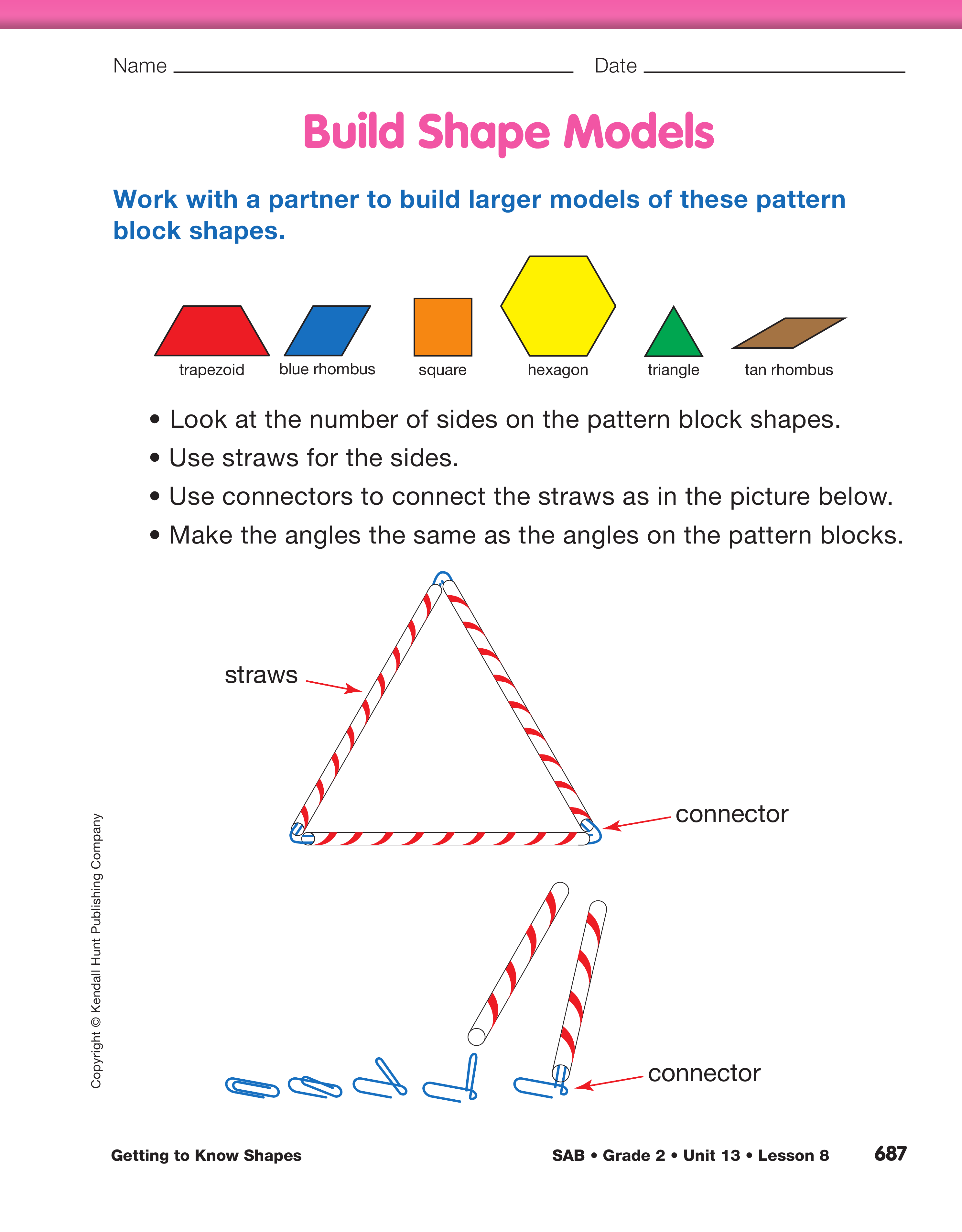
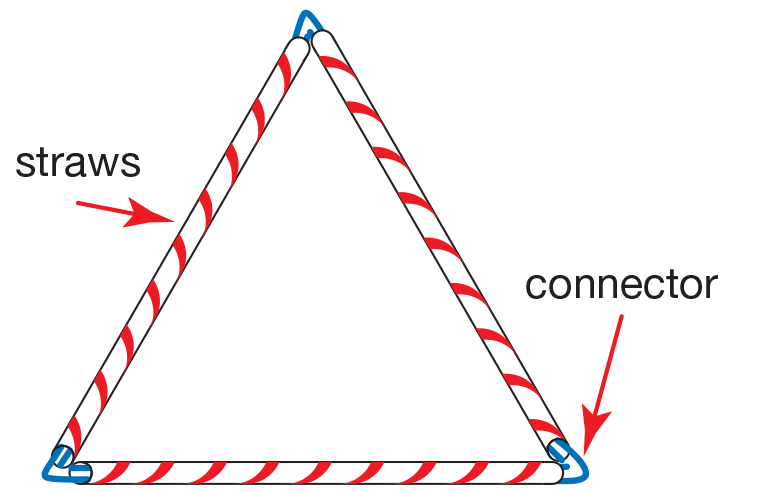
Make Pattern Block Shape Models. Direct students
to the directions on the Build Shape Models
page in the Student Activity Book. Tell student pairs
that they will be making larger models of the pattern
block shapes using straws of the same length and
chenille sticks (or paper clips) to connect the straws.
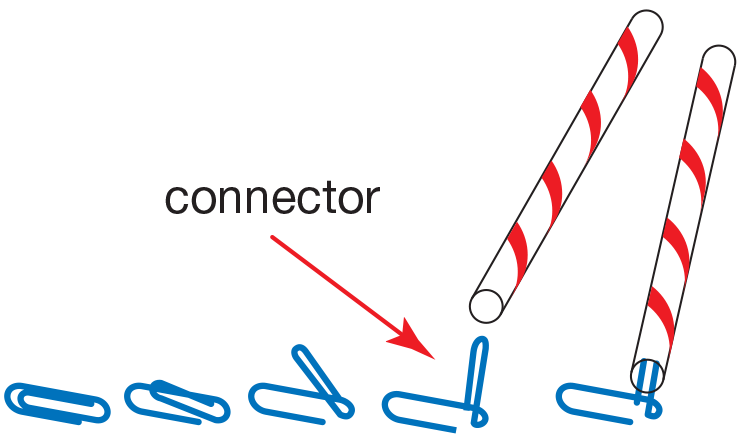
See Figure 2. The connectors in Figure 2 are made
from chenille sticks. Figure 3 illustrates how to
make connectors from paper clips. To help students
get started, show them one way to connect the
straws. However, allow them to make the models on
their own.
Before they begin building, ask students to think
about the number and relative length of the sides in
each shape. Some students may be puzzled about
how long to make the longest side of a trapezoid.
Encourage students to compare the lengths of the
sides of the pattern blocks. They should notice that
all the sides are of equal length except for the long
side, which is twice as long as the other sides of the
trapezoid.
- Which shapes have sides that are all the same
length? (square, rhombuses, hexagon, triangle)
- Which shape has sides that are different lengths? (trapezoid)
- Compare the side length of the triangle to the side
length of the hexagon. Are they the same? (yes)
- Compare the side length of the blue rhombus to
the side length of the square. Are they the same? (yes)
- Are all the sides of the shapes the same length? (Possible response: All the shapes have the same
length sides expect for the trapezoid. One side of
the trapezoid is longer.)
- What does each straw represent? (a side of the
shape)
- Will you need the same number of straws for each
shape? Why or why not? (No, because the shapes
don't have the same number of sides.)
- Which shape do you think will take the most
straws? Why? (The hexagon because it has
6 sides.)
- If you use one straw for the short sides of the
trapezoid, what could you use for the long side? (Possible response: maybe 2 straws)
- How can you find out how much longer the long
side of the trapezoid is than the short side? (Possible response: You could use a ruler or compare
it to the other pattern blocks.)
Students should notice that all the sides of the other
pattern blocks are of equal length and that this length
is the same as the length of the trapezoid's short
sides. They can lay blocks beside the trapezoid's
long side to see that it is twice as long as the short
sides. See Figure 4. So, if the short sides are made
with one straw each, then the long side should be
made with two straws.
The sides of students' models will be longer than the
pattern block sides, but they should try to make the
angles the same size as the angles of the corresponding
pattern block shapes. This way the models will
be larger than the pattern blocks but the same shape.
Demonstrate how students can connect two straws to
make an angle and lay them on top of the pattern
block to reproduce the angle. See Figure 5.
If the shape keeps falling apart, try using 2 chenille sticks at
each vertex to create a tighter fit.
Regular Polygons. The square, triangle, and hexagon
pattern blocks are special shapes called regular polygons.
Regular means all their sides are of the same length and all
their angles are congruent (of the same measure). Not all
triangles and hexagons are regular. See Figure 6 for
examples. Because these pattern block shapes are special,
some of the properties students observe might not be
generalizable to all shapes of the same name. For example,
not all triangles have congruent angles, even though the
green pattern block triangle does. We introduce a greater
variety of shapes in future lessons.
Describe and Sort Shape Models. After student
pairs construct the models, ask them to place the
shapes on their desks so they can easily see each
shape. Instruct students to use an adhesive note or
piece of paper and tape to label each shape with its
name.
Then pose the following questions:
- Which shape was the easiest to make and why? (Possible response: The square because it had
four square corners.)
- Which shape was the hardest to make and why? (Possible response: The rhombuses because I had
to be careful about the angles. If I made the
angles different, I got different shapes.)
- Which shape has sides that are different lengths? (trapezoid)
- Which shapes have angles that are all the same
size? (square, hexagon, triangle) [See Content
Note.]
- Which shapes are alike? How are they alike? (Possible response: the trapezoid, rhombuses,
and squares all have 4 sides and 4 corners.)
- How are the shapes different from one another? (Possible response: The square's corners are different
from all of the other shapes' corners.)
Compare Quadrilaterals. Now instruct students to
focus on the four-sided shapes.
Ask questions that
help students compare the quadrilaterals:
- Can you find other shapes besides the square that
have four sides? (trapezoid, both rhombuses)
- Are they alike in any other way? (They also have
4 angles.)
- How are the rhombuses and the square alike? How
do you know? (All four of their sides are the
same length. We used the same size straw for
each side.)
- How are the rhombuses and the square different? (The angles of the square are all the same size
and they are L-shaped. The angles of the rhombuses
are different.)
- How is the trapezoid different? (The trapezoid's
sides are not all the same length. Three sides are
the same length and one side is twice as long as
each of the other three.)
Besides the obvious difference in the number of
sides and corners, there is another very important
"dynamic" difference—the triangle is rigid while the
others are not. If you hold one side of the square still
and push on the opposite side, the square can be
deformed into either of the rhombuses. See Figure 7.
The hexagon is even more flexible. This is one reason
that certain structures, such as bridges, are often
built with more-rigid triangles.
Tell students that a square has four square corners or
right angles.
- Do you see any other shapes in your set that have
right angles like the square? (no)
- Can you easily change a square to look like a
rhombus? If so, what changes? (Yes; the angles
or corners change.)
The term "square corner" may be easier for students because
they can understand that a square fits in each corner. Some
students may have misconceptions about the term "right
angle." For example, students might think that "right angle"
means the angle on the right side. Use the terms "square
corner" and "right angle" interchangeably.
Explain that although we refer to the blue and tan
pattern blocks as the blue rhombus and the tan rhombus,
the square is a rhombus as well. Ask students to
adjust the square (the one made from straws) so that
it looks like the blue rhombus and the tan rhombus.
See Figure 7.
- What changed? What stayed the same? (The
angles are not square corners [right angles] anymore.
The four sides still have equal length.)
- If you changed the angles in the rhombus, would
the lengths of the sides still be the same? (Yes,
the lengths of the sides are still the same even
with different angles.)
- If you changed the angles in the rhombus, would
your different shape still be a rhombus? (Yes, it's
a rhombus if all four sides have the same lengths.
The angle size doesn't matter.)
- Look at the rhombuses you made. How are your
rhombuses different? (Possible response: Some
have big, wide angles and some have small,
pointy angles.)
Display and use examples of the students' shape
models to discuss more of the properties of the
shapes. Ask students to look at the square, blue
rhombus, and tan rhombus. Students noticed that
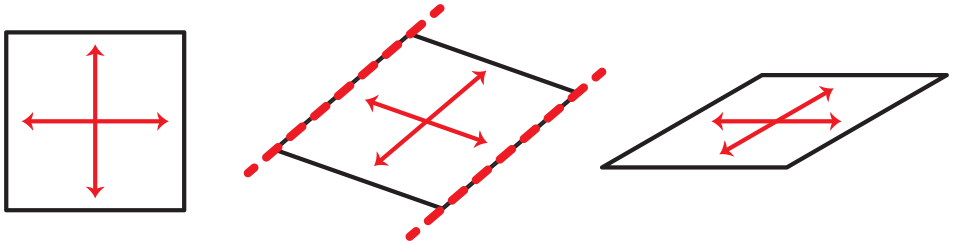
these shapes all have sides that are the same length.
Instruct them to look at the sides directly opposite of
each side and ask what they notice. The opposite
sides are parallel. See Figure 8. Compare the opposite
sides on these shapes to railroad tracks, the
opposite sides of a door, a window, cement blocks in
the wall, or other objects in the classroom. The
opposite sides go in the same direction. If you drew
lines that made the opposite sides go on forever, the
lines would never meet.
- Does the trapezoid have any parallel sides? Show
us. (It has two parallel sides and two sides that
are not parallel.)
- Does the hexagon have any parallel sides? Show
us. (It has 3 sets of parallel sides.)
- Does the triangle have any parallel sides? How do
you know? Show us. (No; the triangle doesn't
have opposite sides that stay the same distance
apart from each other.)