Fraction Puzzles

Est. Class Sessions: 1

Developing the Lesson

Part 2: Puzzling Out Halves

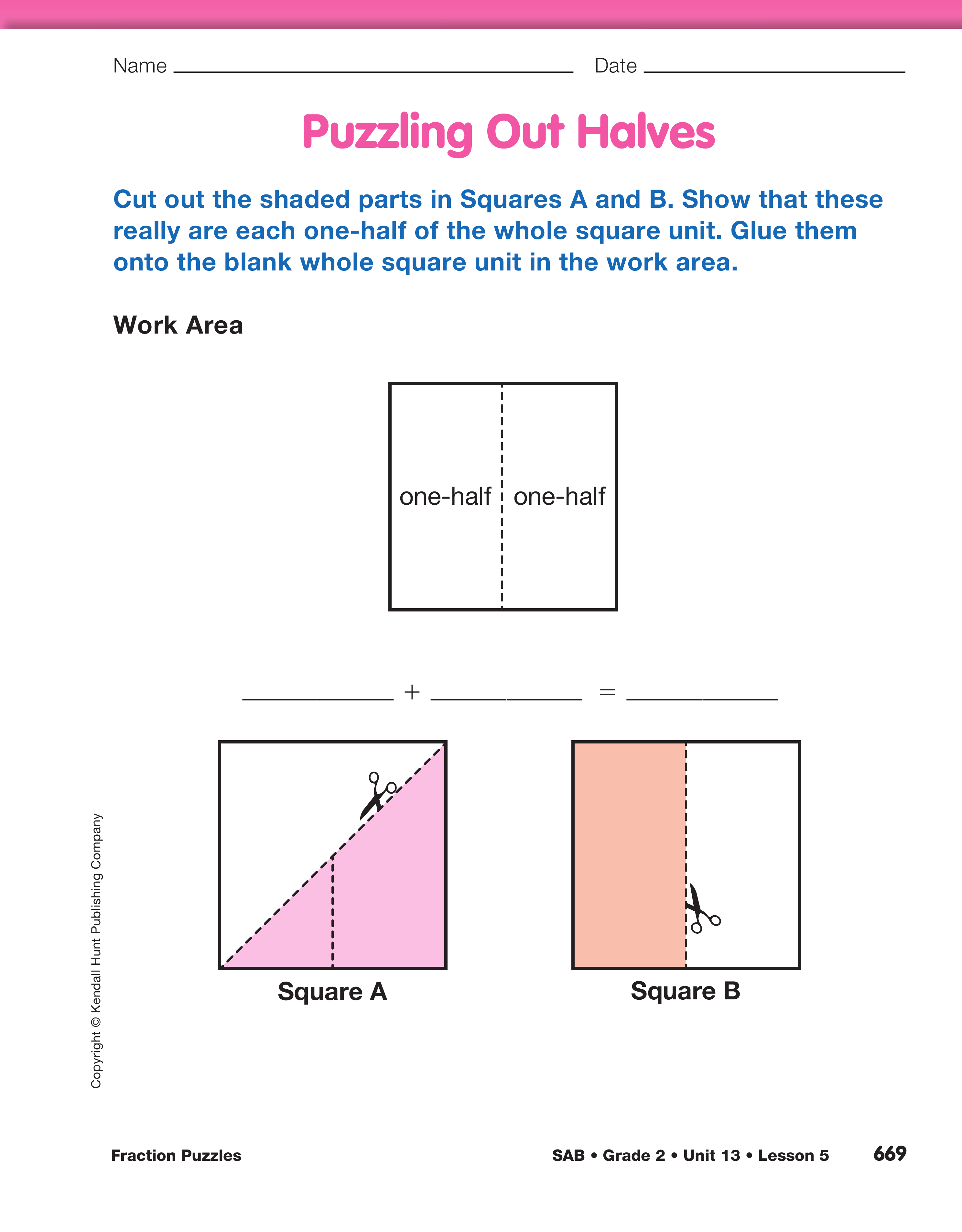
Display the Puzzling Out Halves page in the Student Activity Book. Tell students that the square is one whole unit.

Ask:

What do you notice about Square A and Square B? (Possible response: The shaded part of Square A is a triangle and the shaded part of Square B is a rectangle.)
What part of Square A is shaded? Why do you think so? (one-half; Possible response: If I cut out Square A and fold it on the line, both sides match. That means there are two equal parts.)
Have you seen halves that look like that before? Where? (Possible response: Sometimes my dad cuts my sandwich in half like that.)
Do you think the unshaded part is the same size as the shaded part? Why? (Possible response: Yes, because if you fold it, the two parts match.)
Is the unshaded part also one-half? (yes)
What part of Square B is shaded? Why do you think so? (one-half; Possible response: It is the same as A except you fold it differently.)
Are the shaded and unshaded parts in Square B both one-half? Why do you think so? (Yes; both sides cover the same amount of area.)

Instruct students to cut out the shapes and glue them onto the whole square unit in the Work Area on the Puzzling Out Halves page. Give students time to solve the problem on their own.

Upon completion, ask a student volunteer to display his or her solution. If necessary, model the solution by cutting out the shaded parts on your copy of the Puzzling Out Halves page and fitting the two pieces together. Students will see that both the shapes on the top of the page are exactly half of the whole square unit.

Adventure Book:

Student Activity Book: 669

Answers