Solve Puzzle 1. The following fraction puzzle activities
will offer students informal experiences adding
one-half and one-fourth through visual representations
and cutout activities. Display and direct students
to the One-Half Plus One-Fourth 1 page in the
Student Activity Book. Explain that the class is going
to work on some puzzles.
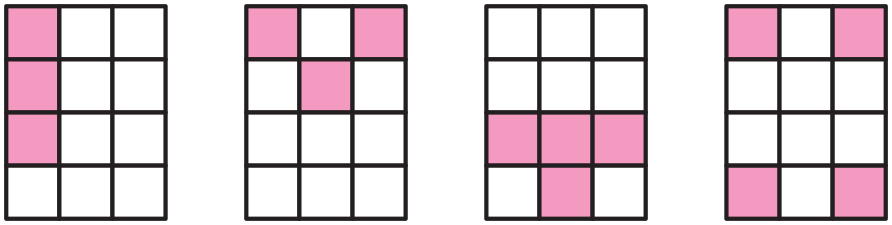
- Look at Square C. What part of the square is
shaded? (one-half)
- What part of Square D is shaded? How do you
know? (one-fourth; Possible response: Square D
is divided into 4 smaller squares and one of the
four squares is shaded.)
- Are all the smaller squares in Square D the same
size? How do you know? (Possible response: If I
use my ruler and connect the tick marks, I can
draw a grid on the Square D. Then I can count
the smaller squares. Each of the four squares has
4 very small squares so I know they are all the
same size.)
- Compare Squares C and D to Square A. What do
you see?
- Do you think the same amount of area is shaded in
C and D as is shaded in A? Why do you think so?
- What can you do to prove it? (Possible responses:
Draw grid lines on the squares; cut out the
shaded parts and match them up.)
Challenge students to cut out the shaded parts of
Squares C and D and use the cutout parts to construct
a shape in Square B that looks like the shaded
part of Square A. Use your extra copy of the
One-Half and One-Fourth 1 page to cut out the
shaded parts in Squares C and D. After students have
had a chance to solve the puzzle, have a student
demonstrate the solution on the display.
- How much of Square A is covered? Point to each
fourth on the display and count. (three-fourths)
- Is the same amount of area shaded in C and D as
is shaded in A? Show us why you think so. (Possible response: When I place the cutout
pieces on top of the shaded part in Square A, the
same amount of space is covered.)
- Does one-half plus one-fourth equal three-fourths?
Explain why you think so. (Square C covers
one-half of the large square. Square D covers
one-fourth of the large square. If I put them
together, three-fourths of a large square will be
covered like in Square A.)
- Can anyone prove this in a different way? (Possible response: I can imagine grid lines on all
of the squares. The shaded part of Square C is
8 little squares and the shaded part of Square D is
4 little squares. Together, 12 little squares is the
same amount that is shaded in Square A.)
Solve Puzzle 2. Direct students to turn to the
One-Half Plus One-Fourth 2 page in the Student
Activity Book. Again, start by asking them to identify
the fractions represented in Squares C and D.
- Look at Square C. What part of the square is
shaded? (one-half)
- What part of Square D is shaded? Why do you
think so? (one-fourth; Possible response: It is
one-fourth even though it is a different-shaped
fourth than the one in the first puzzle. There are
four equal columns. It is one of four equal parts
so it is a fourth.)
- Can fourths be different shapes but still cover the
same area? (Possible response: I think so. I
remember that we cut the sandwich squares into
different shapes, but they were all still fourths.)
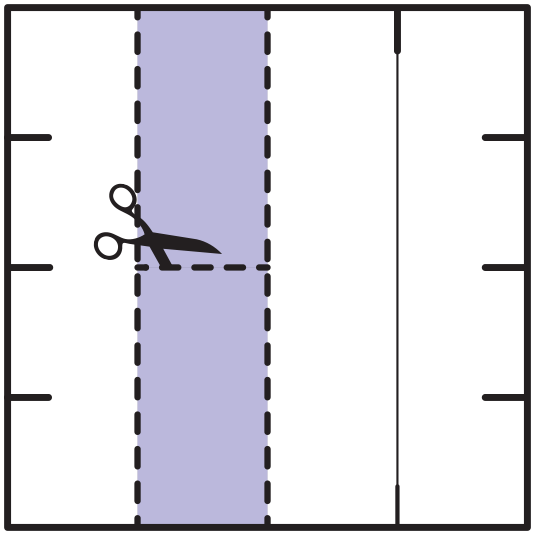
See if students can decide how to alter the
column-shaped fourth in Square D so it can be put
together to cover one-fourth of Square A. See Figure
1. When they finish, review the puzzle as a class and
invite students to share their solution strategies.
Compare this puzzle with the previous one.
- What do you notice when you compare this puzzle
with the first puzzle? (Even though the fourths are
different, they still cover the same amount of
space.)