Cover Rectangles with Tiles. Begin the lesson by
assigning the Cover Rectangles pages in the Student
Activity Book. Explain that students will cover a
whole rectangle with square-inch tiles, and then
cover one-half, one-third, or one-fourth of the rectangle.
Cover One-Half. Upon completion, use the 4 Sides and 4 Corners 1 Master to discuss Questions 1–2 on
the Cover Rectangles page. Students can record their
responses on the Master. Students will need square-inch tiles and a ruler.
- This is the shape you covered in Questions 1–2.
What is this shape called? (rectangle)
- How many sides does a rectangle have? Point to
the sides. (four sides)
- How many square corners does a rectangle have?
Point to the square corners. (four)
- Who would like to show how to use a ruler and
measure the sides of the rectangle? (The rectangle
has two sides that are 3 inches long and
two sides that are 4 inches long.)
- How many square-inch tiles did you use to cover
the rectangle? (12 tiles)
- Show how you covered one-half of the rectangle.
How many tiles did you use? [See Figure 1.] (6 tiles)
- How did you figure out how many tiles were
needed to cover half of the rectangle? (Possible
response: There are 12 tiles and I know that half
of 12 is 6.)
- How many squares are left uncovered? (6 squares)
- Who can show us a different way to cover one-half
of the rectangle? How many tiles did you use? [See Figure 1.] (6 tiles)
- Do all of the ways we have discussed cover half
the rectangle? How do you know? (Possible
response: If 6 tiles are used, then half of the rectangle
is covered no matter what the shape
because 2 fair shares of 12 is 6, and 6 + 6 = 12.)
Use tiles to model one of the examples shown in
Figure 1 on the 4 Sides and 4 Corners 1 Master.
Discuss whether or not this way covers one-half of
the rectangle. Students should recognize that equal
shares of the same whole do not have to be the same
shape. In all of the examples, 6 tiles are still covering
half of the rectangle.
Cover One-Fourth and One-Third. Using the display,
have student volunteers show and record how to
cover one-fourth of the rectangle. Then use the same
display and questioning to discuss covering one-third
of the rectangle. See Figure 2.
- How many tiles did you use to cover [one-fourth]
of the rectangle? (3 tiles)
- How many squares were left uncovered? (9 tiles)
- Did anyone show [one-fourth] a different way?
How many tiles did you use? (3 tiles)
- How did you decide how many tiles were needed
to cover [one-fourth] of the rectangle? (Possible
response: I thought about equal shares. I knew
there were 12 tiles in the whole rectangle. I figured
that to share 12 tiles fairly among 4, each
part needed 3 tiles. 3 + 3 + 3 + 3 = 12.)
Compare Rectangles and Squares. Display the top
part of the 4 Sides and 4 Corners 2 Master. Students
can record their responses on the Master.
- What is this shape called? (square)
- Does this square have four sides like a rectangle?
Does it have four square corners like a rectangle? (yes)
- Can this square also be a rectangle? (yes)
Explain that a square is a special kind of rectangle.
Ask students to measure one of their tiles to determine
each side's length. Students will discover that
the square has four equal sides and four square corners,
therefore making it both a square and a rectangle.
- How is a square the same as a rectangle? (They
both have 4 sides and they both have 4 square
corners.)
- How is a square different from a rectangle? (A square's sides are all the same length and a rectangle's
sides don't have to be.)
- How many tiles are needed to cover the square I
have displayed? (9 tiles)
- You need to cover one-third of the square. Is there
something you could add to this drawing to make
it easier to see a third? (grid lines like the rectangle)
Partition Rectangles into Rows and Columns. Demonstrate how to use a ruler to connect the tick
marks to draw a grid on the 4 Sides and 4 Corners 2
Master.
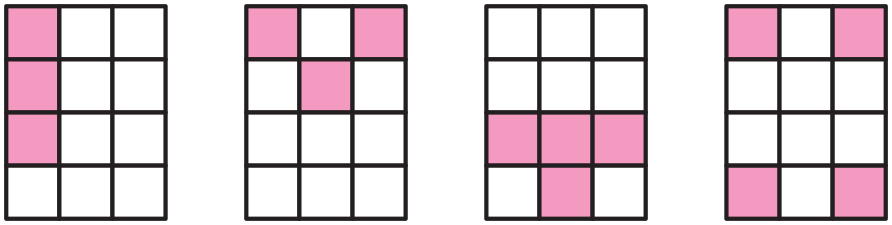
- Now show how to cover one-third of the square.
How many tiles are needed? [See Figure 3 for
examples.] (3 tiles)
- How did you decide how many tiles to use to cover
one-third of the square? (Possible responses: I
took 9 tiles and made 3 equal shares of 3; I
looked at the grid and could see that 3 tiles made
a column that was one-third of the shape.)
- Show another way to cover a third of the square.
How do you know that your way covers one-third? [See Figure 3.] (Possible responses: A whole is
three-thirds and since two-thirds are uncovered, I
know one-third is covered; 9 tiles cover the whole
square and 9 shared equally among 3 makes
thirds. There are 3 tiles in each third; I know
3 + 3 + 3 = 9, so I can look at 9 and know 3 is
one-third of it.)
- A third of this square is 3 tiles, but do thirds
always have 3 things in them? Explain. (No; it just
depends on the whole. A third of 9 is 3, but a
third of 12 is 4.)
Assign the Partition Rectangles pages in the Student
Activity Book for students to complete individually.
Students will use rulers to partition rectangles into
rows and columns and then shade one-half,
one-fourth, or one-third of the shape.
Use the Check-in: Questions 3–5 and the Feedback Box on
the Partition Rectangles pages in the Student Activity Book to
assess students' abilities to partition rectangles into equal
shares [E2]; partition a rectangle into rows and columns of
the same size unit [E3]; use words and models to describe
equal shares [E4]; and recognize that equal shares of the
same whole do not have to be the same shape [E5].