Partition Shapes

Est. Class Sessions: 2–3

Developing the Lesson

Find Fair Shares Less Than One.

To begin the lesson, provide access to paper, colored pencils or crayons, and scissors and ask student pairs to solve the following problem:

Mrs. Murphy has two pies in her bakery. Eight children want to eat them. How can you share the pies fairly so that each child gets the same amount?

Allow students time to find a strategy with which to solve the problem.

Because no one will get a whole pie, students will likely partition each pie into fourths.

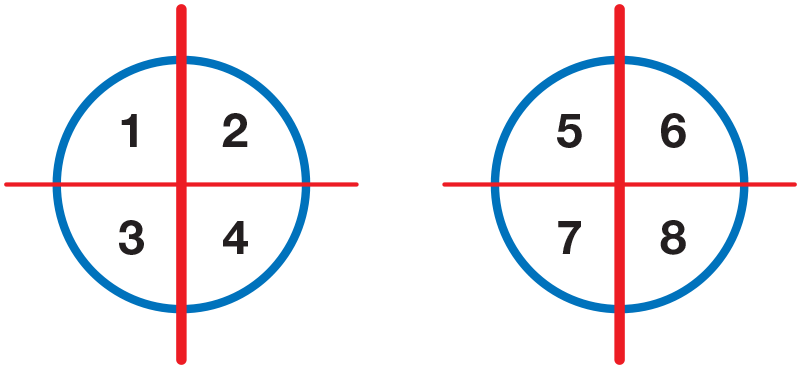
Did anyone use a model to help them solve the problem? (Possible response: 2 paper circles to represent the pies; a drawing)
How did you solve the problem? How much pie does each child get? (Possible response: There was not enough for everyone to get a whole pie. I halved each pie. There was not enough, so I halved the halves and each pie had four fourths. I gave each child a fourth.) [See Figure 2.]
Is it reasonable that each child got less than one whole pie? Why or why not? (Yes, because there were less pies than children. There weren't enough pies for everyone to get a whole pie.)

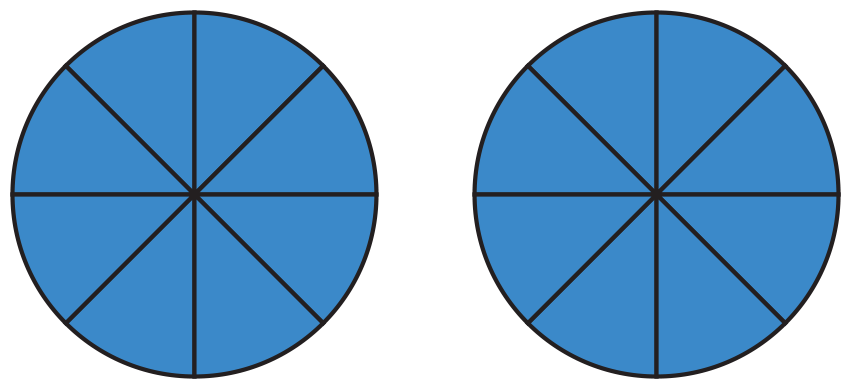
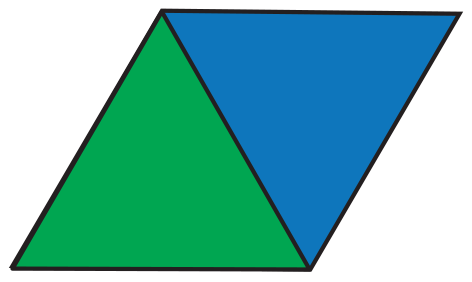
Some students might solve the problem by dividing each pie into eight pieces, and give each child two-eighths. See Figure 3.

If a child solves the problem this way, he or she might ask if two of eight pieces is the same as one-fourth. Use models to compare each student's strategy. See the Sample Dialog below:

Teacher: How did you solve this problem?

Ana: I divided each pie into 4 pieces, so I had 8 pieces altogether. I gave each child one-fourth of a pie.

Johnny: I cut each pie into 8 slices. Then I gave each child one slice from each of the two pies. Each child gets two-eighths. Is that the same as Ana's answer?

Teacher: If I take the two-eighths and place it on top of the one-fourth, is it the same?

Johnny: Yes, it is! So two-eighths is the same as one-fourth.

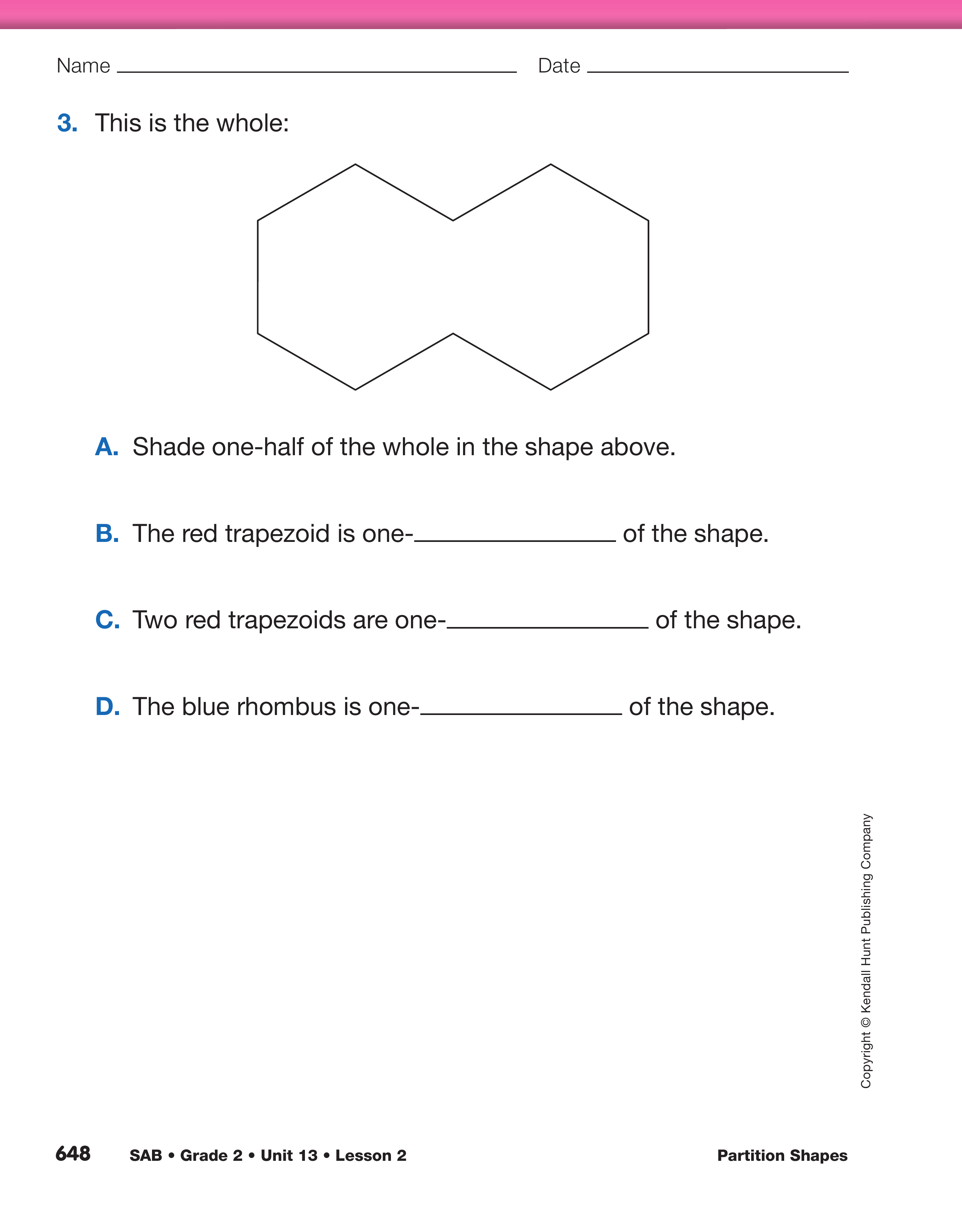
Partition Shapes into Two Fair Shares. Distribute sets of pattern blocks to students. See Materials Preparation. Instruct students to use their set of pattern blocks to solve the following problems. Display a yellow hexagon.

Ask:

Mrs. Murphy baked a cake that was shaped like this yellow hexagon. How can you share this cake between two people?
How much cake does each person get? (a half)
What shape covers half the cake? (red trapezoid)
In this problem, what is the shape of the whole cake? (yellow hexagon)

Next tell the students that the shape of the cake has changed. Now the whole is the blue rhombus. Give students time to use their pattern blocks to solve the following problem.

Display a blue rhombus and say:

Mrs. Murphy made a special blue rhombus cake that looks like this. How can you share this cake between two people?
How much cake does each person get? (a half)
What shape covers half the cake? (green triangle)
What is the shape of this whole cake? (blue rhombus)
Has the whole changed? (yes)

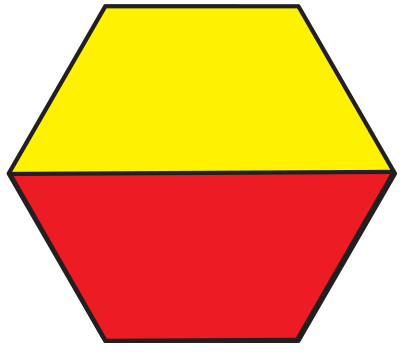
Display a yellow hexagon with one red trapezoid covering half the shape. See Figure 4.

Ask:

Is this red trapezoid half of a yellow hexagon? How do you know? (Yes; Possible response: I know it is half because it takes two red trapezoids to completely cover the yellow hexagon. So each trapezoid is one half of the hexagon.)

Display a blue rhombus with one green triangle covering half the shape. See Figure 5.

Ask:

Is this green triangle half of a blue rhombus? How do you know? (Yes; Possible response: I know it is half because it takes two green triangles to completely cover the blue rhombus. So each triangle is one-half of the rhombus.)

Leave the pattern blocks on display to help students recognize that the same fractional parts, in this case halves, of different-size unit wholes are not equal.

Direct their attention to the red trapezoid as it covers half of the whole yellow hexagon, and to the green triangle as it covers half of the whole blue rhombus.

Ask:

You called the red trapezoid a half and the green triangle a half. How can both of these shapes be halves? (The wholes are different. The red trapezoid is half of the yellow hexagon and the green triangle is half of the blue rhombus. When the wholes are different, the halves are different, too.)

Change the whole one more time. Display a red trapezoid.

Ask:

Mrs. Murphy made this red trapezoid cake for a birthday party. How can you share this cake between two people?
How much cake does each person get? (a half)
What shape covers half the cake? (brown trapezoid)
What is the shape of this whole cake? (red trapezoid)
Has the whole changed again? (yes)
What happens to the halves when the wholes change? (The halves change, too.)
What can you say about halves and wholes, no matter what the shape is? What is always true about a half? (Possible response: When you cut a whole into two equal parts, each part is a half.)

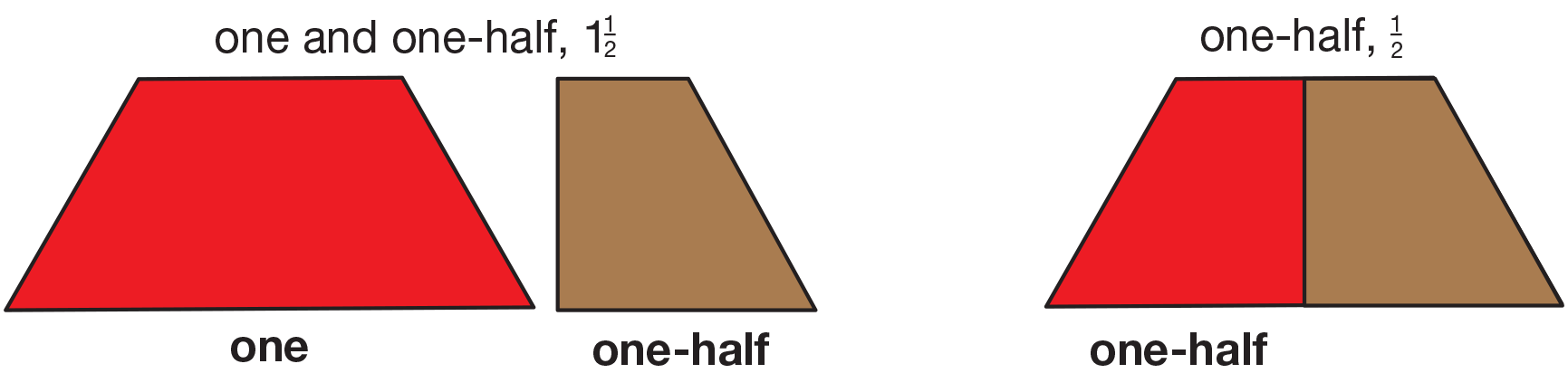
To address a common misconception, encourage students to use the pattern blocks at their desks to model one-half and one and one-half.

Ask:

Is one and a half the same as one-half? Use pattern blocks to explain this. (Possible response: They sound kind of the same but they are not. One and a half means you have a whole thing and another half, too.) [See Figure 6.]
When you say, "One and one-half," what does the "one" mean? (It means one whole.)
What does "and one-half" mean? (It means you have another half to add on.)
When you say just "one half," what does that mean? (One half is one of two equal parts. It is less than one whole.)

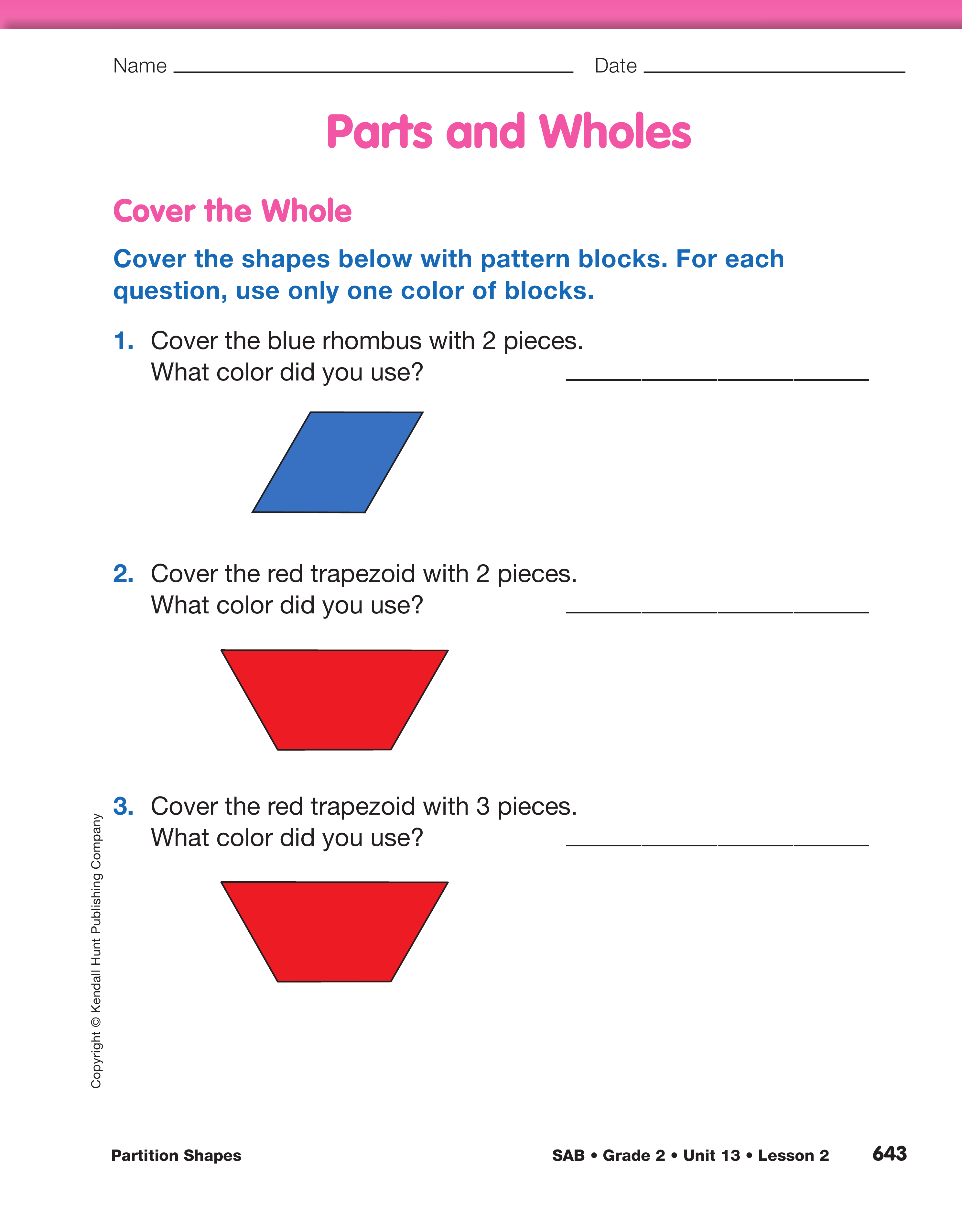
Cover the Whole. Display the red trapezoid again.

Ask:

Cover the red trapezoid with 2 pieces. What color did you use? (brown)
The brown trapezoid is what fraction of the red trapezoid? (one-half)
Now cover the red trapezoid with 3 pieces, all of the same color. What color did you use? (green)
If you shared this red trapezoid cake fairly among three people, how much of the cake would each person get? (one-third)
The green triangle is what fraction of the red trapezoid? (one-third)

Direct students' attention to the Parts and Wholes pages in the Student Activity Book. Assign Questions 1–7 in the Cover the Whole section to student pairs. Students will use pattern blocks of one color to cover shapes.

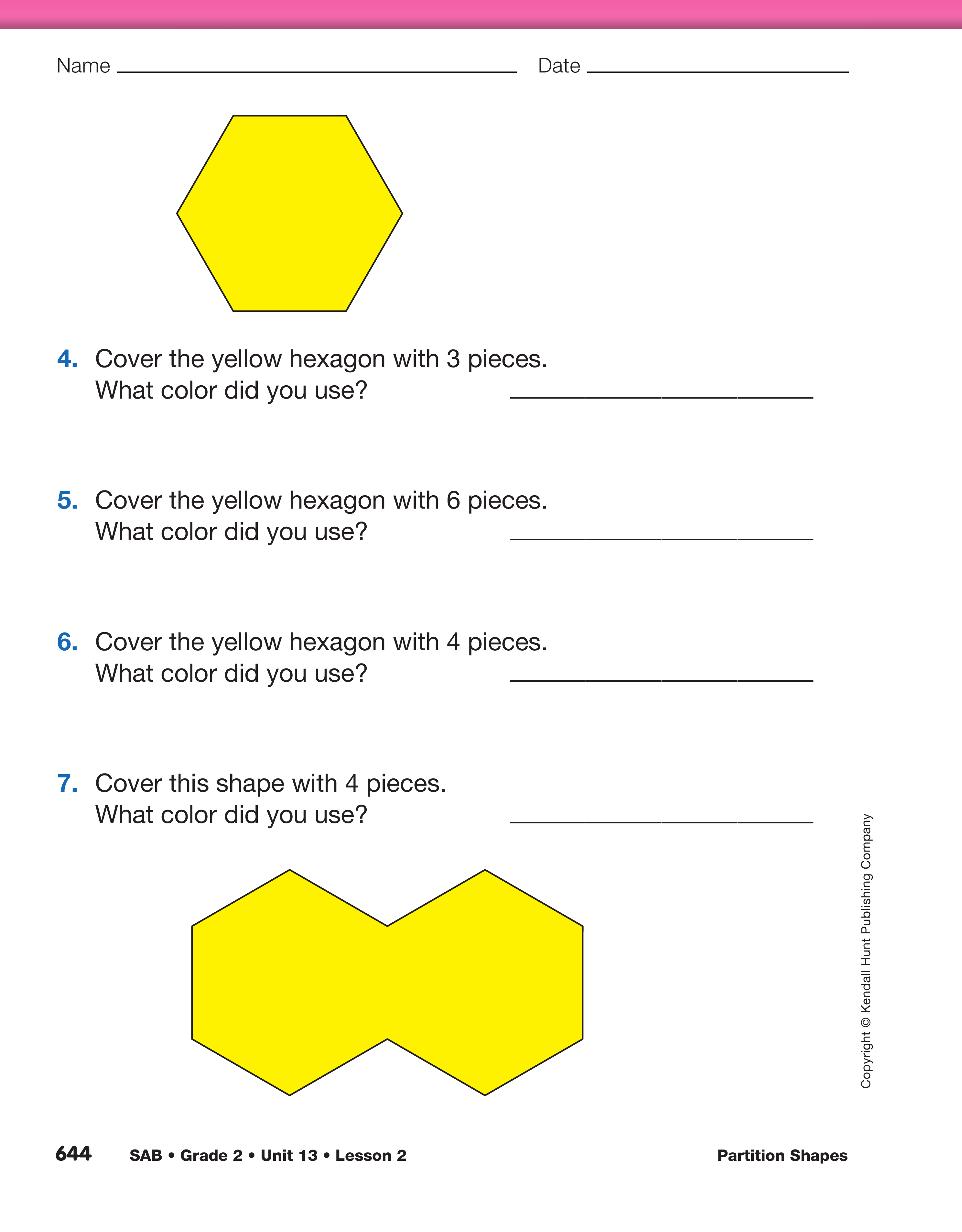
Upon completion, help students make the connection between the number of fair shares and a fraction's name. Display and discuss Questions 5–7 on the Parts and Wholes pages.

Ask:

Look at Question 5. How many green triangles cover the yellow hexagon? (6 green triangles)
Imagine a cake shaped like this yellow hexagon. If you shared the cake equally among 6 people, how much cake would each person get? (Possible responses: a piece shaped like a green triangle; one-sixth of the cake)
The green triangle is what fraction of the yellow hexagon? (one-sixth)
In Question 6, what color did you use to cover the yellow hexagon? (brown)
Imagine sharing this piece among 4 people. Are the pieces larger or smaller than when you shared the hexagon with 6 people in Question 5? (The fourths are larger than the sixths.)
Is this reasonable? Why or why not? (It makes sense. When you share a whole with 4 people, the pieces will be larger than when you share the same whole with 6 people.)
How did you figure out which four pieces covered the shape in Question 7? (Possible response: I knew the shape was 2 yellow hexagons. I reasoned that since 2 red trapezoids cover 1 hexagon, 4 red trapezoids cover 2 hexagons.)
The red trapezoid is what fraction of the shape? (one-fourth)
Imagine a cake shaped like the one in Question 7. If you shared it fairly among 4 people, how much cake would each person get? (a fourth)

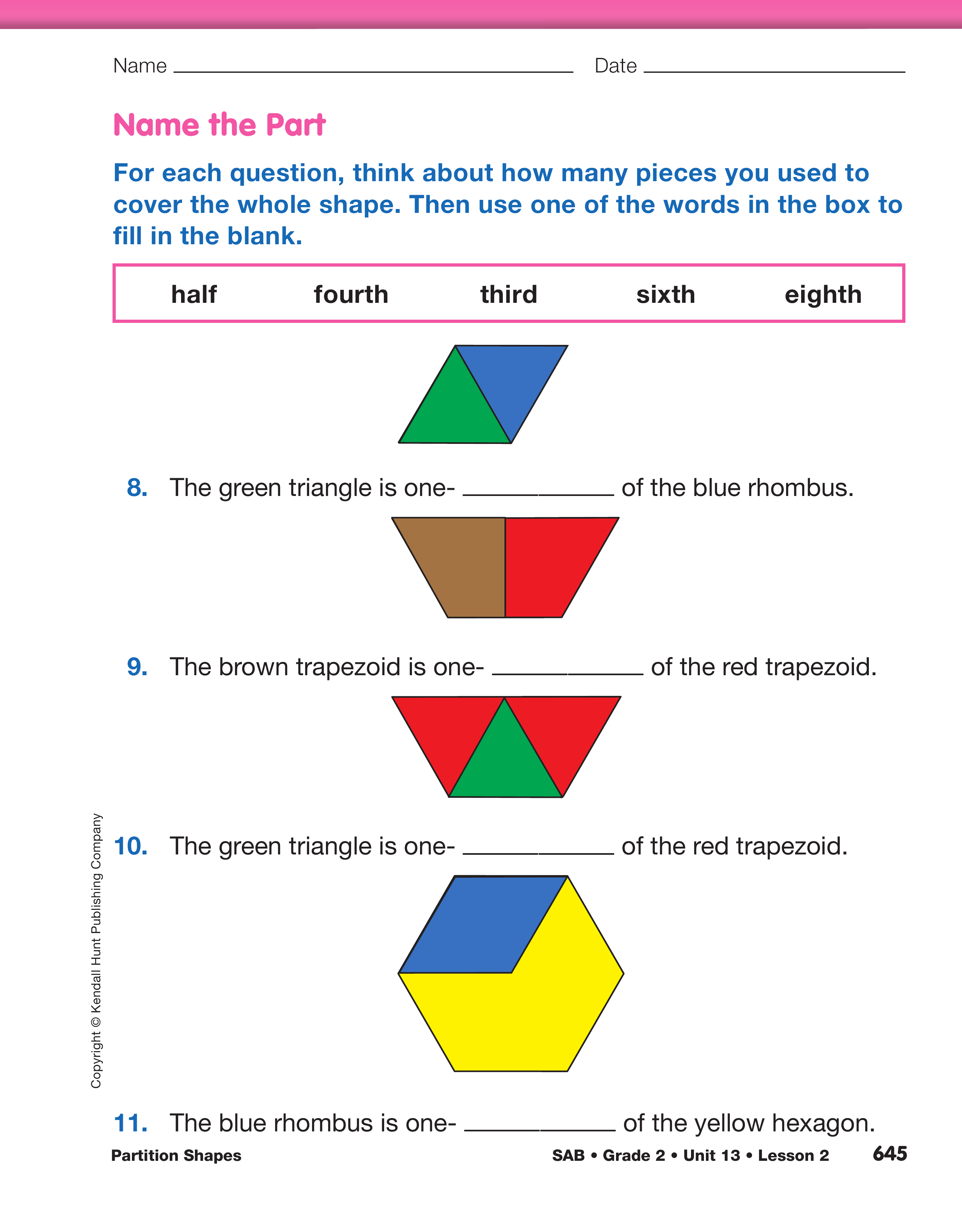
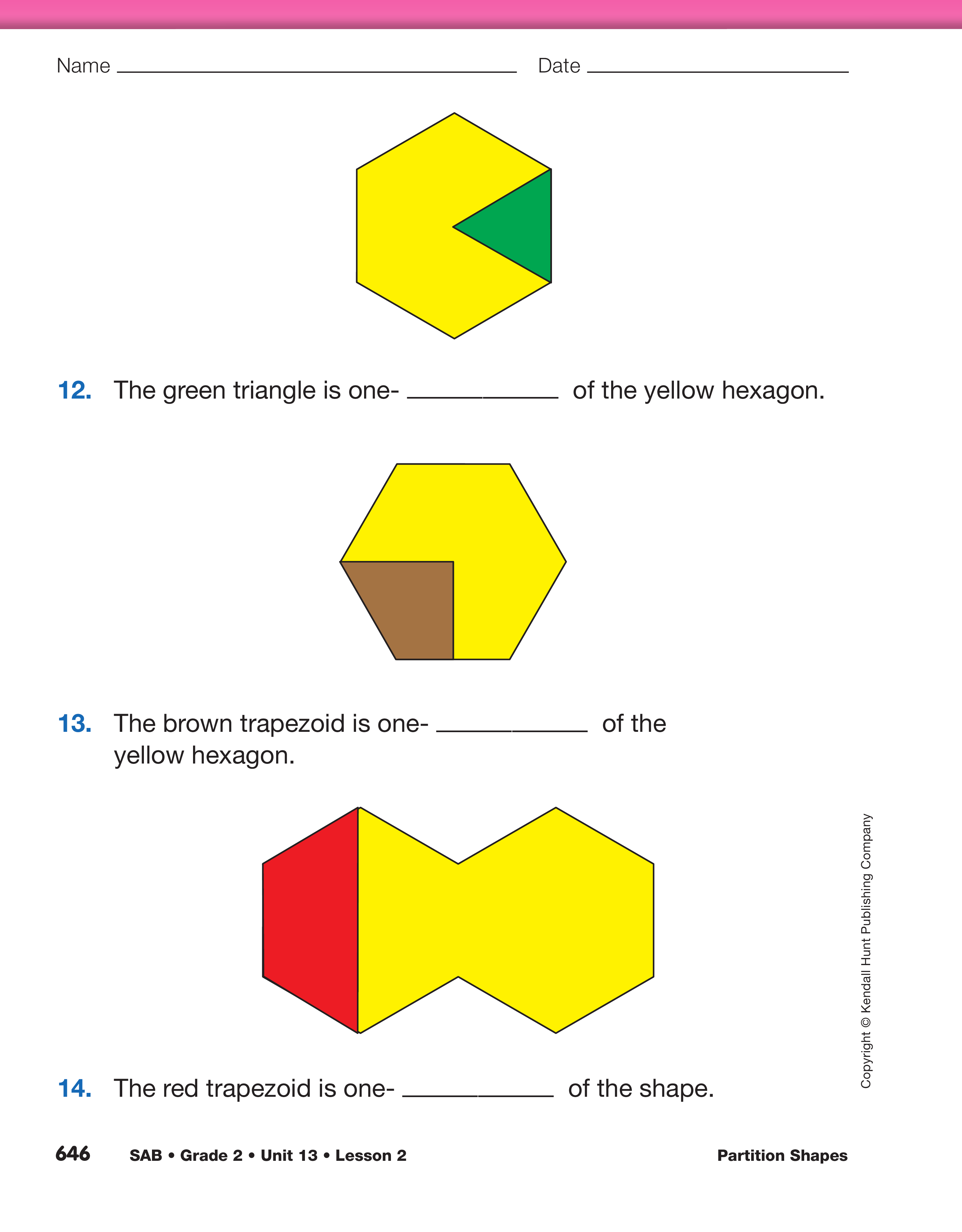
Name the Part. Direct students' attention to the Name the Part section of the Parts and Wholes pages. Assign Questions 8–14. Students name the unit fraction represented in each question. As they work, encourage students to consider the pattern block relationships they explored in Questions 1–7.

Upon completion, discuss Question 11. Because the shape is divided into two parts, students might assume that the blue rhombus represents one-half. It is important to emphasize that fractional parts have to be equal. Three blue rhombuses cover the yellow hexagon, so one rhombus represents one-third.

Show Part of the Whole. Use pattern blocks to display different-shaped wholes. Each time you change the whole, have a student volunteer show which pattern block represents the fractional part you describe. Have students represent the fractions described with the blocks at their desks. Display a blue rhombus.

Ask:

Here is the whole. Which piece is one-half? (green triangle)

Change the whole by displaying the red trapezoid.

Ask:

Here is the whole. Which piece is one-half? (brown trapezoid)
Which piece is one third? (green triangle)

Change the whole by displaying the yellow hexagon.

Ask:

Here is the whole. Which piece is one-half? (red trapezoid)
Which piece is one-third? (blue rhombus)
Which piece is one-fourth? (brown trapezoid)

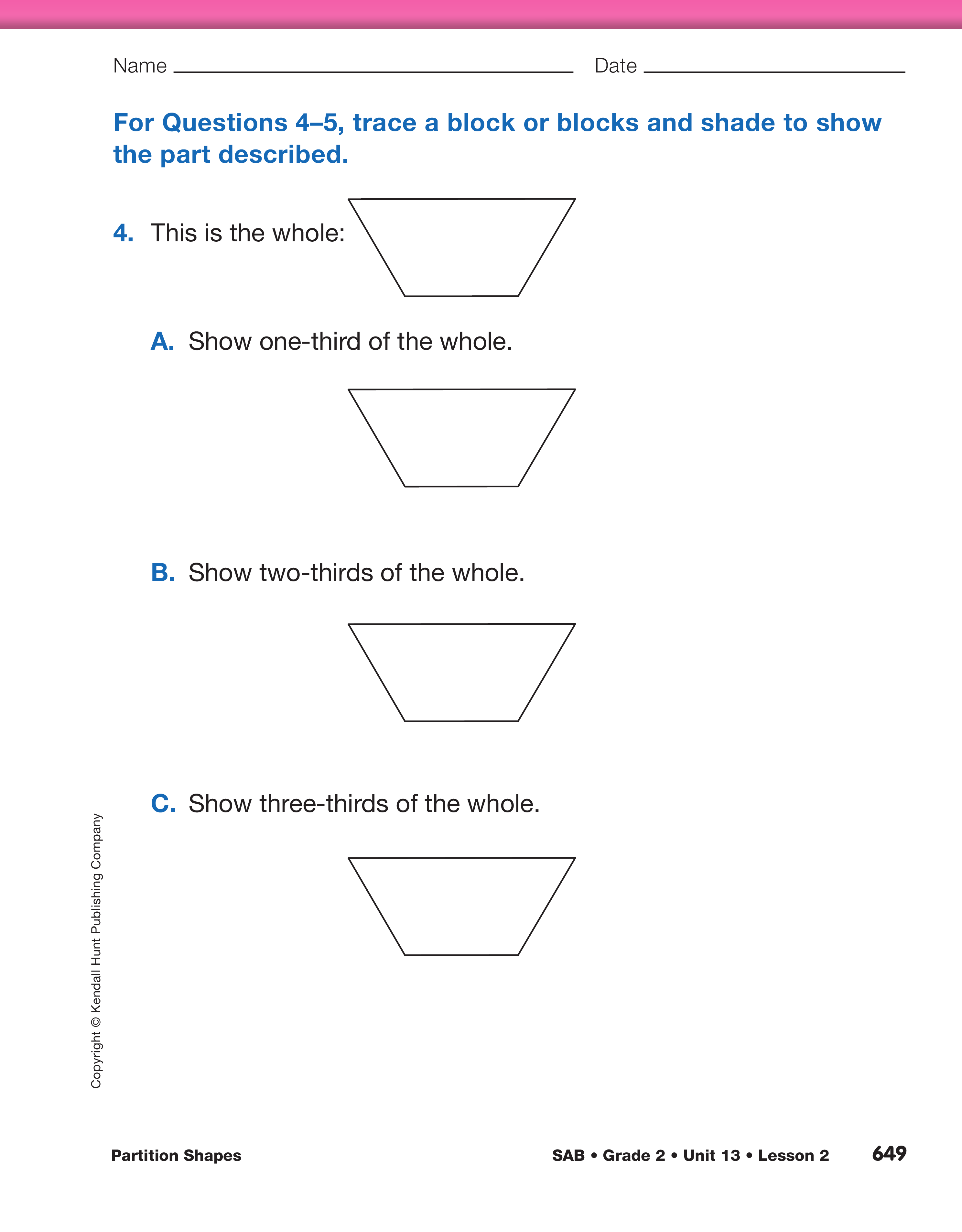
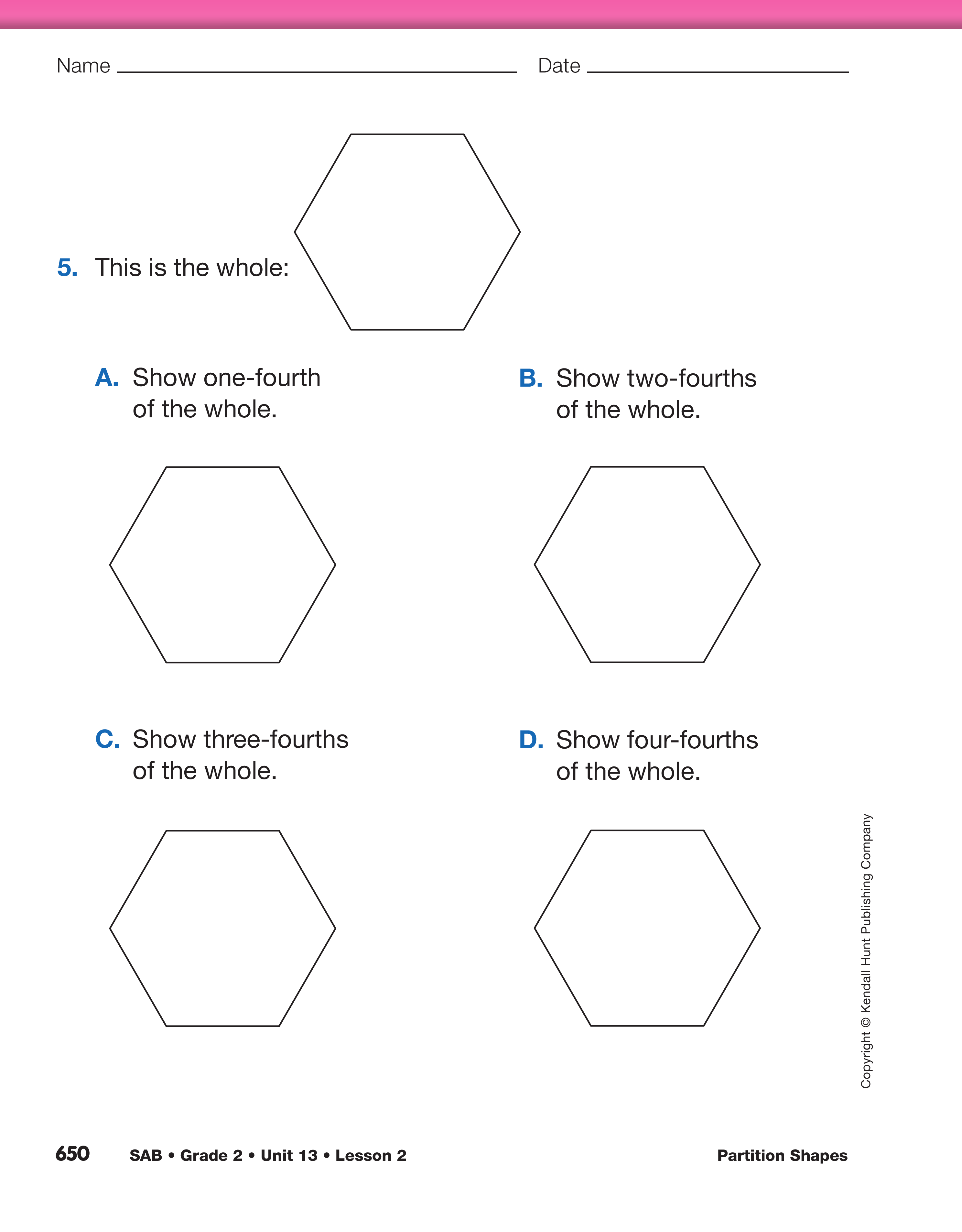
Assign the Show Part of the Whole pages in the Student Activity Book. Students will trace a pattern block or blocks to show the fractional part described. They will also be asked to name the fractional part described.

Use Check-In: Questions 1–3 and the Feedback Box on the Show Part of the Whole pages in the Student Activity Book to assess students' abilities to partition shapes into equal shares [E2]; use words and models to describe equal shares (e.g., half, third, fourth, sixth) [E4]; recognize that the same fractional parts of different-size unit wholes are not equal [E7]; check for reasonableness [MPE3]; and show work [MPE5].

Question 3D on the Show Part of the Whole pages in the Student Activity Book is a challenging question involving sixths that will indicate whether a student is ready to transfer their understanding of fair shares to fractional parts beyond halves, thirds, and fourths.

Adventure Book: